地量见地价？我拿一年的上证数据算了算

股谚云，天量见天价、地量见地价。今天我们就来验证一下。

要把股谚量化，首先要解这道难题：数组中第i个元素是多少周期以来的最小值（最大值）？

---

比如，有数组如下： 1， 2， 2， 1， 3， 0。那么，第1个元素1，是1周期以来的最小值，第2个元素2，是到目前为止的最大值，所以，也是1周期以来的最小值；但第4个元素1则是从第2个元素以来的最小值，所以它是3周期以来的最小值。

依次计算下去，我们得到这样一个序列： 1, 1, 2, 1, 4, 6。其中的每一项，都是原数组中，对应项到目前为止的最小值。

这个算法有什么用处呢？它可以用在下面的计算当中。

比如，有股谚云，天量见天价，地量见地价。

当行情处在高位，成交量创出一段时间以来的天量之后，后续成交量将难以为继，容易引起下跌；当行情处在低位，成交量创出一段时间以来的地量之后，表明市场人气极度低迷，此时价格容易被操纵，从而引来投机盘。在计算地量时，我们就要知道，当前的成交量是多少期以来的最小值。

比如，如果大盘当前的成交量成为了120天以来的最低量，这时候很可能就会引起大家的关注了。要验证出现地量之后，后面是否真的有行情，就需要进行因子分析或者回测验证。现在的问题是，怎么计算呢？

无脑的双重循环

我们以上面的数组为例，最简单的算法是使用循环：

---

def min_range_loop(s):
    minranges = [1]
    for i in range(1, len(s)):
        for j in range(i-1, -1, -1):
            if s[j] < s[i]:
                minranges.append(i - j)
                break
        else:
            minranges.append(i+1)
    return minranges

s = [1,2,2,1,3,0]

min_range_loop(s)

输出为：1, 1, 2, 1, 4, 5

这个算法实现用了双重循环，应该比较耗时。我们生成10000个元素的数组跑一下，发现调用一次需要用时9.5ms。

它山之石，myTT的实现

在myTT中有一个类似的函数实现：

def LOWRANGE(S):                       
    # LOWRANGE(LOW)表示当前最低价是近多少周期内最低价的最小值 by jqz1226
    rt = np.zeros(len(S))
    for i in range(1,len(S)):  rt[i] = np.argmin(np.flipud(S[:i]>S[i]))
    return rt.astype('int')

---

它应该也是实现元素i是多少周期之前的最小值，只不过从注释上看，该函数多在计算最低价时使用。但实际上序列s是什么没有关系。

这个函数用了一个循环，还使用了flipuid函数，比较有技巧。这个函数的用法演示如下：

s = [1, 2, 2, 3, 2, 0]
np.all(np.flipud(s) == s[::-1])

也就是它的作用实际上就是翻转数组。

不过，LOWRANGE函数似乎没有实现它声明的功能，不知道是不是对它的功能理解上有错误。当我们用同一个数组进行测试时，得到的结果与双循环的并不一致。

s = np.array([1, 2, 2, 3, 2, 0])
LOWRANGE(s)

得到的结果是：

array([0, 0, 0, 0, 1, 0])

---

除此之外，如果同样拿10000个元素的数组进行性能测试，LOWRANGE执行时间要60ms，居然跑输给Python双循环。测试环境使用的Python是3.11版本，不得不说Python3.11的优化非常明显。

如果我们要完全消除循环，应该怎么做呢？

烧脑的向量化

如果我们能把数组[1, 2, 2, 3, 2, 0]展开为：

$\displaystyle \left[\begin{matrix}1.0 & \text{NaN} & \text{NaN} & \text{NaN} & \text{NaN} & \text{NaN}\\1.0 & 2.0 & \text{NaN} & \text{NaN} & \text{NaN} & \text{NaN}\\1.0 & 2.0 & 2.0 & \text{NaN} & \text{NaN} & \text{NaN}\\1.0 & 2.0 & 2.0 & 3.0 & \text{NaN} & \text{NaN}\\1.0 & 2.0 & 2.0 & 3.0 & 2.0 & \text{NaN}\\1.0 & 2.0 & 2.0 & 3.0 & 2.0 & 0.0\end{matrix}\right]$

然后实现一个函数，接收该矩阵输入，并能独立计算出每一行最后一列是多少个周期以来的最小值，这个问题就得到了求解。

要实现这个功能，我们可以通过numpy的masked array和triu矩阵来实现。

---

n = len(s)
mask = np.triu(np.ones((n, n), dtype=bool), k=1)
masked = np.ma.array(m, mask=mask)
masked

triu中的k参数决定了生成的三角矩阵中主对角线的位置。k=0,对角线取在主对角线上；k<0，对角线取在主对角线之个k个单位；k>0，对角线取在主对角线之上k个单位。

我们将得到以下输出：

masked_array(
  data=[[1.0, --, --, --, --, --],
        [1.0, 2.0, --, --, --, --],
        [1.0, 2.0, 2.0, --, --, --],
        [1.0, 2.0, 2.0, 3.0, --, --],
        [1.0, 2.0, 2.0, 3.0, 2.0, --],
        [1.0, 2.0, 2.0, 3.0, 2.0, 0.0]],
  mask=[[False,  True,  True,  True,  True,  True],
        [False, False,  True,  True,  True,  True],
        [False, False, False,  True,  True,  True],
        [False, False, False, False,  True,  True],
        [False, False, False, False, False,  True],
        [False, False, False, False, False, False]],
  fill_value=1e+20)

mask flag为True的部分将不会参与运算。如果我们把masked转给sympy，就可以验证这一点：

---

from sympy import Matrix

n = len(s)
mask = np.triu(np.ones((n, n), dtype=bool), k=1)
masked = np.ma.array(m, mask=mask)
Matrix(masked)

我们得到了与期望中一样的展开矩阵。

$\displaystyle \left[\begin{matrix}1.0 & \text{NaN} & \text{NaN} & \text{NaN} & \text{NaN} & \text{NaN}\\1.0 & 2.0 & \text{NaN} & \text{NaN} & \text{NaN} & \text{NaN}\\1.0 & 2.0 & 2.0 & \text{NaN} & \text{NaN} & \text{NaN}\\1.0 & 2.0 & 2.0 & 3.0 & \text{NaN} & \text{NaN}\\1.0 & 2.0 & 2.0 & 3.0 & 2.0 & \text{NaN}\\1.0 & 2.0 & 2.0 & 3.0 & 2.0 & 0.0\end{matrix}\right]$

现在，我们要求解的问题变成，每一行最后一个数是多少周期的最小值。我们进行一个变换：

s = np.array([1, 2, 2, 3, 2, 0])
diff = s[-1] - s
rng = np.arange(len(diff))
rng - np.argmax(np.ma.where(diff > 0, rng, -1))

---

我们用最后一个元素减去数组，然后再比较元素是否大于零，如果大于零，我们就将值设置为索引(rng)，否则设置为-1，然后再通过argmax找到最后一个非零值。这样输出元素的最后一个值，就是最小周期数。在此例中是5。

如果s = np.array([1, 2, 2, 3, 2]),那么计算出来的最后一个值是4。 如果s = np.array([1, 2, 2, 3])，这样计算出来的最后一个值是1。 依次类推。这刚好就是在masked array中，按axis = 1计算的结果。

下面是完整的代码：

def min_range(s):
    """计算序列s中，元素i是此前多少个周期以来的最小值"""
    n = len(s)

    diff = s[:,None] - s
    mask = np.triu(np.ones((n, n), dtype=bool), k=1)
    masked = np.ma.array(diff, mask=mask)

    rng = np.arange(n)
    ret = rng - np.argmax(np.ma.where(masked > 0, rng, -1), axis=1)
    ret[0] = 1
    if filled[1] <= filled[0]:
        ret[1] = 2
    return ret

---

我们来验证一下结果：

s = np.array([1, 2, 2, 3, 2, 0])
min_range(s)

输出结果是1, 1, 2, 1, 4, 6

在最后一个数字上，与loop略有差异。不过，如果是用来寻找地量条件，这个数值一般要比较大才生效，所以，有一点误差可以接受。

消除了两个循环，性能应该有很大的提升吧？

遗憾的是，在同样的测试条件下，这个函数需要822ms，比双循环慢了100倍。花了这么多功夫，还引入了一点小误差，许诺的性能提升不仅没有实现，反而更糟糕了。真是意外啊。

地量见地价？

最后，我们以上证为例，看看这个算法的实际作用。

import akshare as ak
df = ak.stock_zh_index_daily(symbol="sh000001")

df_one_year = df.tail(250)
df_one_year["minrange"] = min_range_loop(df_one_year["volume"].to_numpy())

ax = df_one_year.plot(x='date', y='close', label='close', color='blue', secondary_y=False)
df_one_year.plot(x='date', y='minrange', label='Min Range', color='red', secondary_y=True, ax=ax)

这里我们使用了akshare数据源，所以，所有人都可以复现。

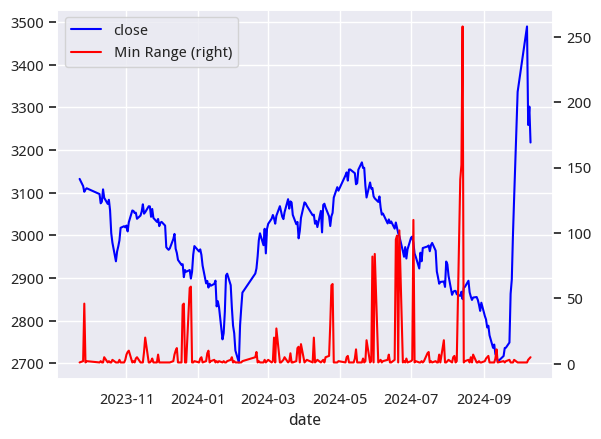
我们得到的输出如下：

这个图显示了惊人的结果。几乎在每一次地量（大于50天）出现之后，都能立刻迎来一个小的反弹。但大级别的反弹，还需要在地量之后，随着资金不断进场，成交量放大才能出现。

比如，在8月底，上证出现了一年以来的最低地量，随后立即迎来一个小反弹。在反弹失败之后，其它指标也逐渐见底回升，最终迎来了9月底的十年不遇的暴涨行情。

《因子投资与机器学习策略》喊你上课啦！

面向策略研究员的专业课程，涵盖因子挖掘、因子检验和基于机器学习的策略开发三大模块，构建你的个人竞争优势！

课程助教: 宽粉
1. 全网独家精讲 Alphalens 分析报告，助你精通因子检验和调优。
2. 超 400 个独立因子，分类精讲底层逻辑，学完带走 350+ 因子实现。
3. 课程核心价值观：Learning without thought is labor lost. Know-How & Know-Why.
4. 三大实用模型，奠定未来研究框架¹：聚类算法寻找配对交易标的（中性策略核心）、基于 XGBoost 的资产定价、趋势交易模型。
5. 领先的教学手段：SBP（Slidev Based Presentation）、INI（In-place Notebook Interaction）和基于 Nbgrader（UCBerkley 使用中）的作业系统。

---

1. 示例模型思路新颖。未来一段时间，你都可以围绕这些模型增加因子、优化参数，构建出领先的量化策略系统。