当交易员用上火箭科学!波和导数检测出艾略特浪、双顶及及因子构建

这篇文章的部分思想来自于 John Ehlers。他曾是雷神的工程师,当年是为NASA造火箭的。他有深厚的数字信号处理(DSP)技术背景,为石油钻探发明了最大熵频谱分析(MESA)。这种分析方法能为短暂的地震回波提供高分辩率的显示。
随后,他把这种方法应用到金融领域,并开创了名为MESA的软件公司,为交易者提供相关分析软件和教育服务。
他和JM Hurst是在证券的周期分析上贡献最大的几人之一。John Ehlers还发表了许多专著,包括《交易者的火箭科学》等。
不过,直到1989年Python才被发明,直到千禧年左右才广为人知,所以,John Ehlers的许多思想,是使用一种所谓的Easy Language表达的。我们尝试使用Python来传达他的一些思想,并加入了自己的理解与拓展。最后,我们将介绍基于这种思想,发现的一个因子。
毫无疑问,证券价格是一种变形的周期信号。它的基本走势由公司的价值决定,叠加交易产生的波动。
加速成长的公司,比如,正在浪头上的科技股,它们的价值曲线可能是指数函数,比如90年代的思科、2000年前后的微软,后来的苹果和现在的英伟达。基础服务类的公司,它们的价值曲线应该是参照GDP增长的直线。
Info
说到苹果,最近发布的 Mac Mini 4是相当不错。正在抢购中。几年前入手的 Macbook M1压缩mp4视频能达到6:1的加速比,Mac Mini 4估计加速比能到30:1甚至更高了,也就是1小时的影片,应该不到2分钟完成编码压缩完成。
波动则由不同风格、不同资金管理周期(其倒数即为频率)的投资者驱动。这两类曲线合成了最终的走势,并且重大事件将改变周期规律。
下面这个函数将生成一个震荡向上的价格序列。它由一条向上的直线和一个sine曲线合成。
1 2 3 4 5 6 7 8 9 10 | |
这将生成以下图形:
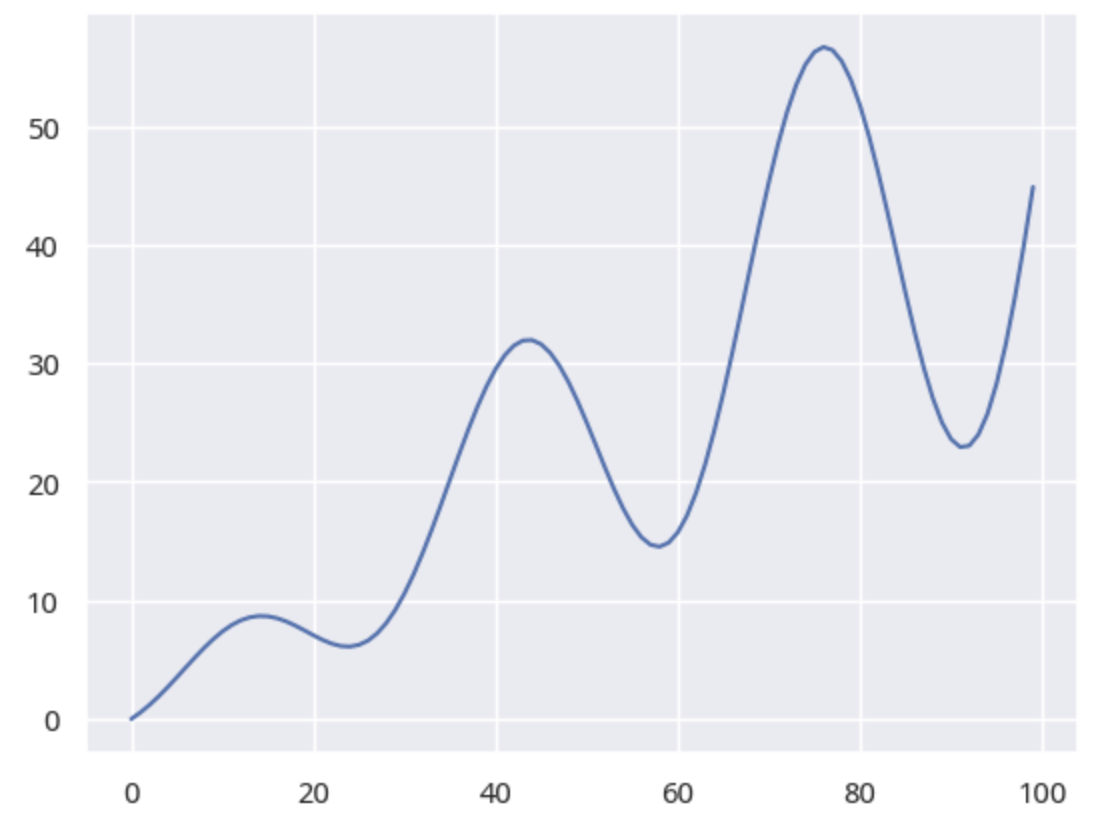 图1. 震荡向上走势
图1. 震荡向上走势
实际上,我们已经合成了一个艾略特驱动浪:
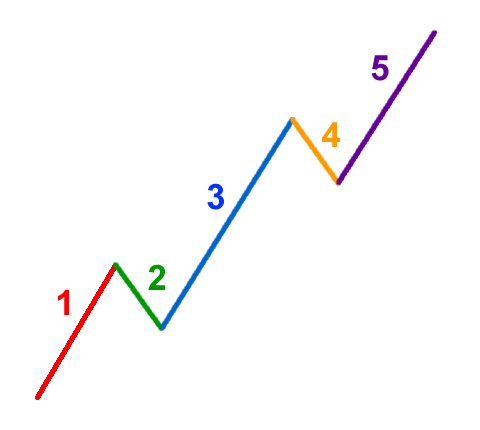 艾略特上升5浪
艾略特上升5浪
合成双顶和头肩顶¶
关于双顶和头肩顶,我有很好的检测算法。不过,如果你对波更感兴趣的话,我可以用sine函数来捏一个。
1 2 3 4 | |
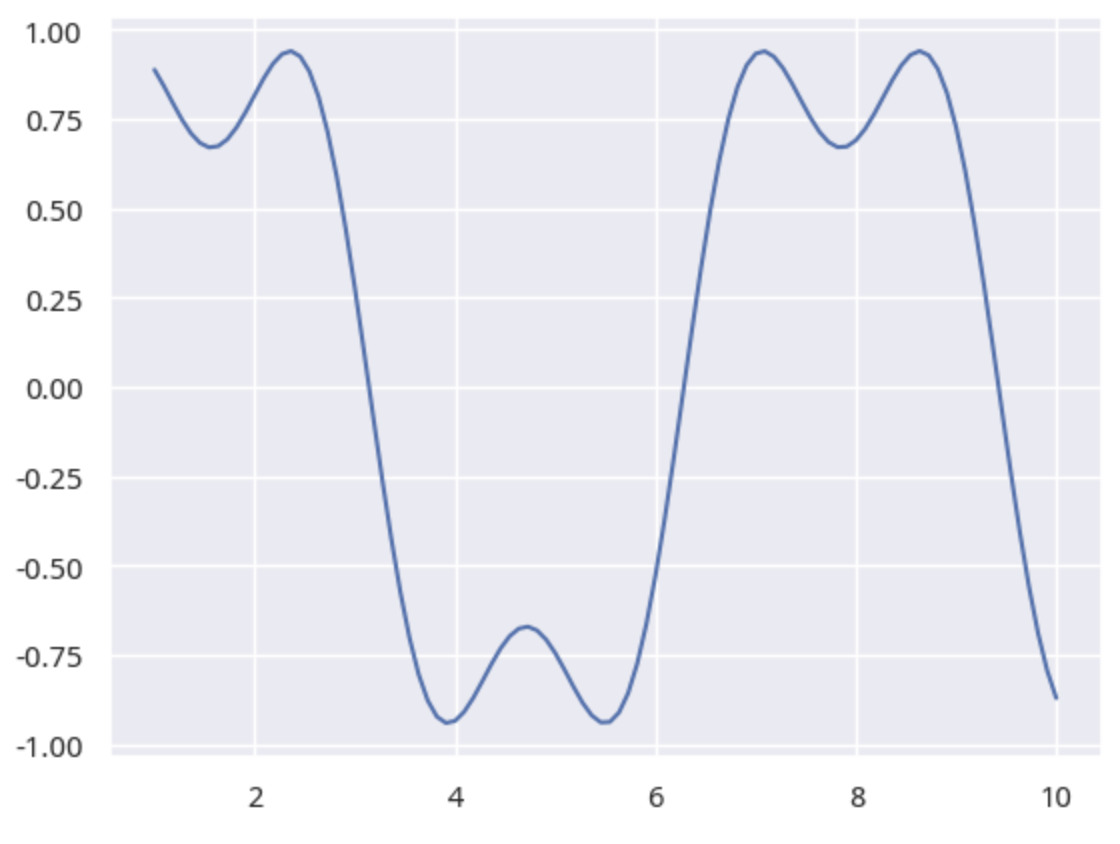 图2 双头
图2 双头
头肩顶只需要再加一个sine波:
1 2 3 4 | |
 图3 头肩顶
图3 头肩顶
如果要检测股价序列中,是否存在双头,我们可以使用scipy中的curve_fit函数。既然\(np.sin(x) + .33 * np.sin(3*x)\)能拟合出双头,那么,如果我们能从价格序列中,通过curve_fit找出类似的函数,再判断参数和估计误差,就能判断是否存在双头。
这个函数泛化后,应该表示为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | |
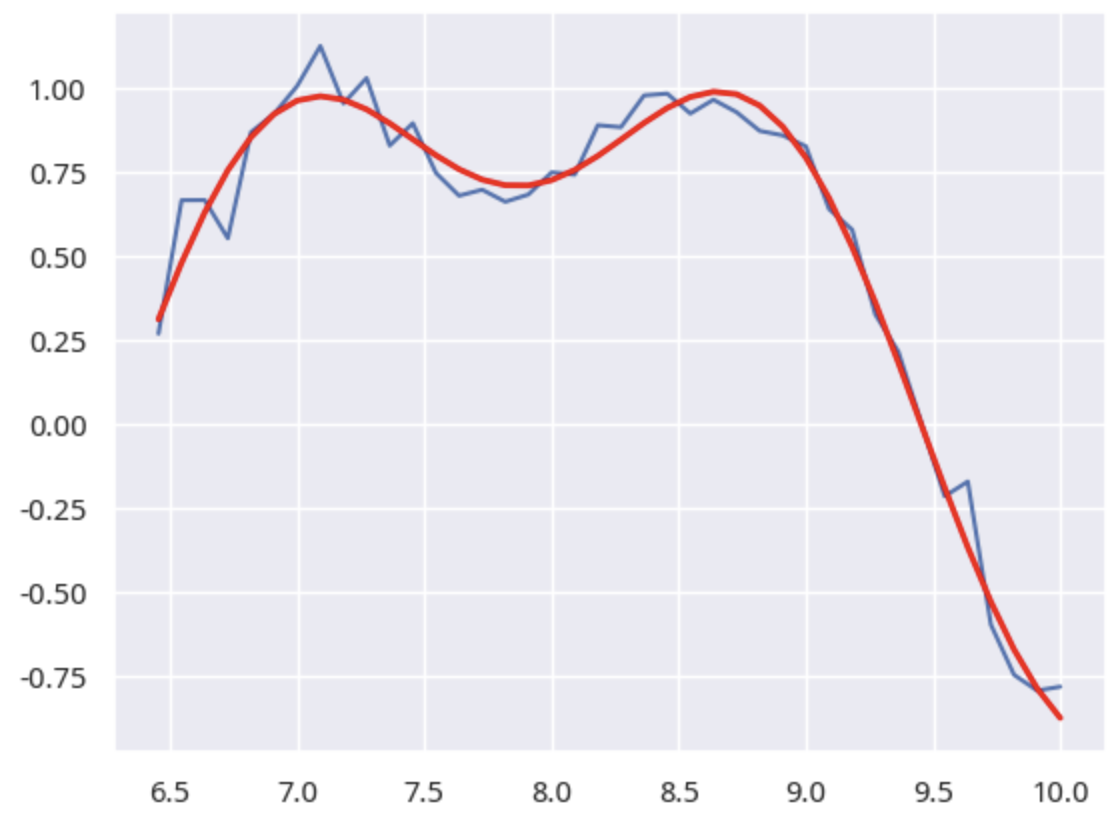 图4 双头推断
图4 双头推断
这里使用了差分进化算法来自动发现参数。
我们把蓝色部分当成是真实的股价序列,红色曲线就是通过差分进化算法推断出来的拟合曲线。
波和导数¶
到目前为止,我们还只进行了铺垫和前戏,只是为了说明股价序列确实具有波的特性。既然如此,我们把波的一些特性给用起来。
正弦波有一个有意思的特性,就是它的导数是一个余弦波,即:
\(\frac{d}{dt}sin(\omega t)=(\frac{1}{\omega})\times cos(\omega t)\)
求导之后,变成频率相同的余弦波,而余弦波是相位提前的正弦波。我们来验证一下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
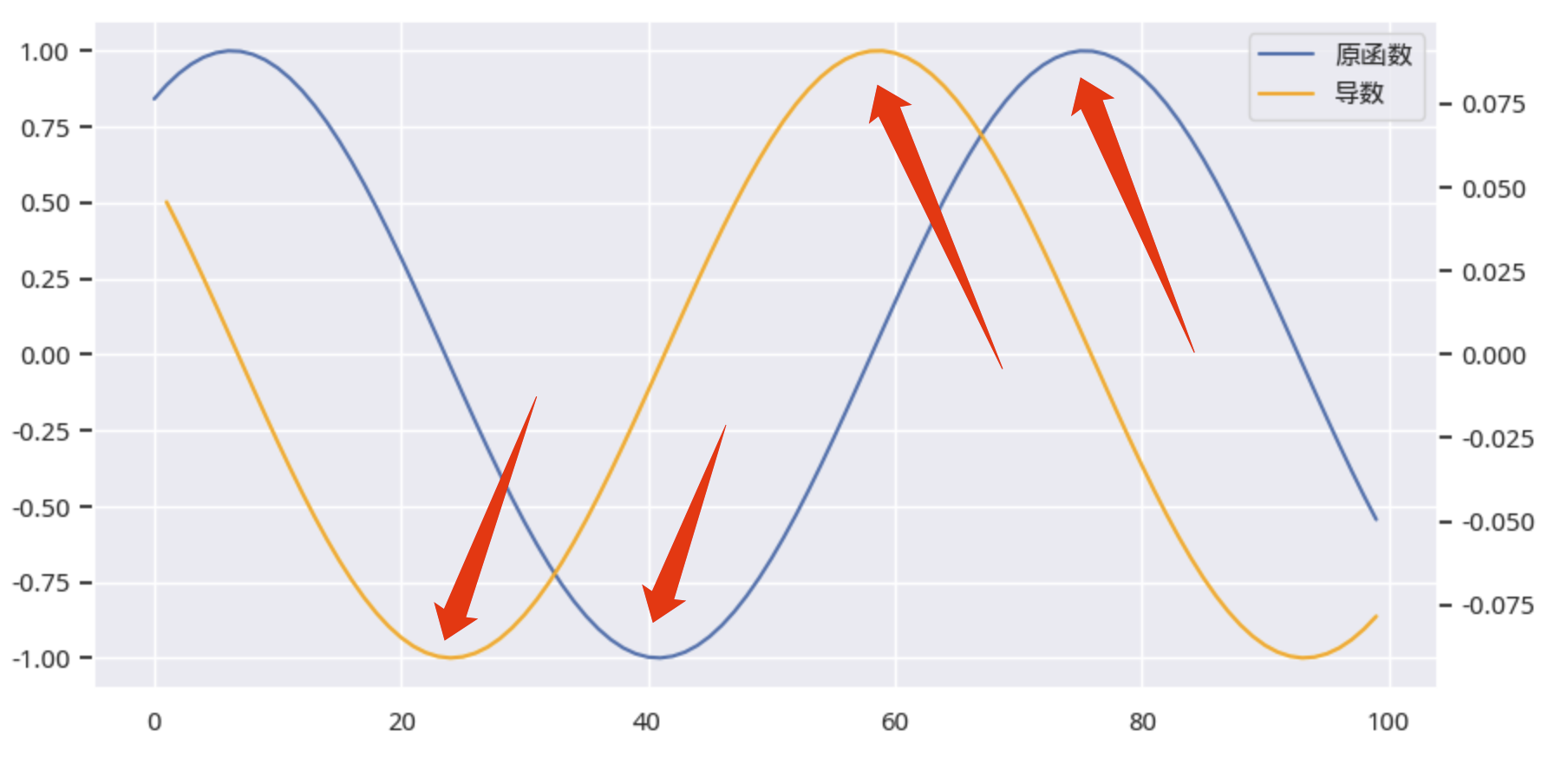 图5 导函数与原函数关系
图5 导函数与原函数关系
蓝色的线是原来的股价,黄色的则是它的导数。从图中可以看出,求导之后,频率不变,振幅变小了,相位提前,并且黄色线的每一个波峰和波谷,后面都对应着蓝色线的波峰和波谷。这意味着什么呢?
如果原函数是一个波函数,现在,我们就能提前预测波峰和波谷了。上图清楚地显示了这一点。
几乎所有的技术指标都是落后指标,但是,导函数居然帮我们预言了波峰与波谷的到来!
Tip
不要感到震惊!其实很多量化人都已经在一种浑然不知的状态下使用这个特性了。比如,你几乎肯定用过三周期的np.diff再加np.mean。只要你用了np.diff数据,就在某种程度上使用了导数。但是,清楚地知道这一特性,我们才知道何时使用、何时放弃。
让我们把话说得再明白一点:
如果原函数是一个波函数,那么,通过寻找导函数的波峰与波谷(这是利用已经发生的数据),就能提前1/4周期知道原函数何时到波峰与波谷 -- 惟一的前提是,规律在这么短的时间里,不发生改变 -- 不会总是这样,但总有一些时间、一些品种上,规律确实会保持,而你要做的,就是运用强大算力,尽快发现它们。
我们将在《因子分析与机器学习策略》课程中,将这个特性转换成一个特征,加入到机器学习模型中,以提高其对顶和底的预测能力。课程还在进行中,现在加入,会是未来几个月中,价格最低的时候。
课程助理小姐姐在这里等你!

不过,在构建机器学习模型之前,我们可以先用这个特性构建一个因子。
我使用2018年到2023年间随机抽取的2000支个股,进行了因子验证,得到以下结果:
| 1D | 5D | 10D | |
|---|---|---|---|
| Ann. alpha | 0.138 | 0.096 | 0.078 |
| beta | 0.036 | 0.064 | 0.058 |
| Mean Period Wise Return Top Quantile (bps) | -1.180 | -1.613 | -1.580 |
| Mean Period Wise Return Bottom Quantile (bps) | -15.671 | -11.045 | -9.155 |
| Mean Period Wise Spread (bps) | 14.491 | 9.531 | 7.650 |
6年间的累计年化收益图如下:
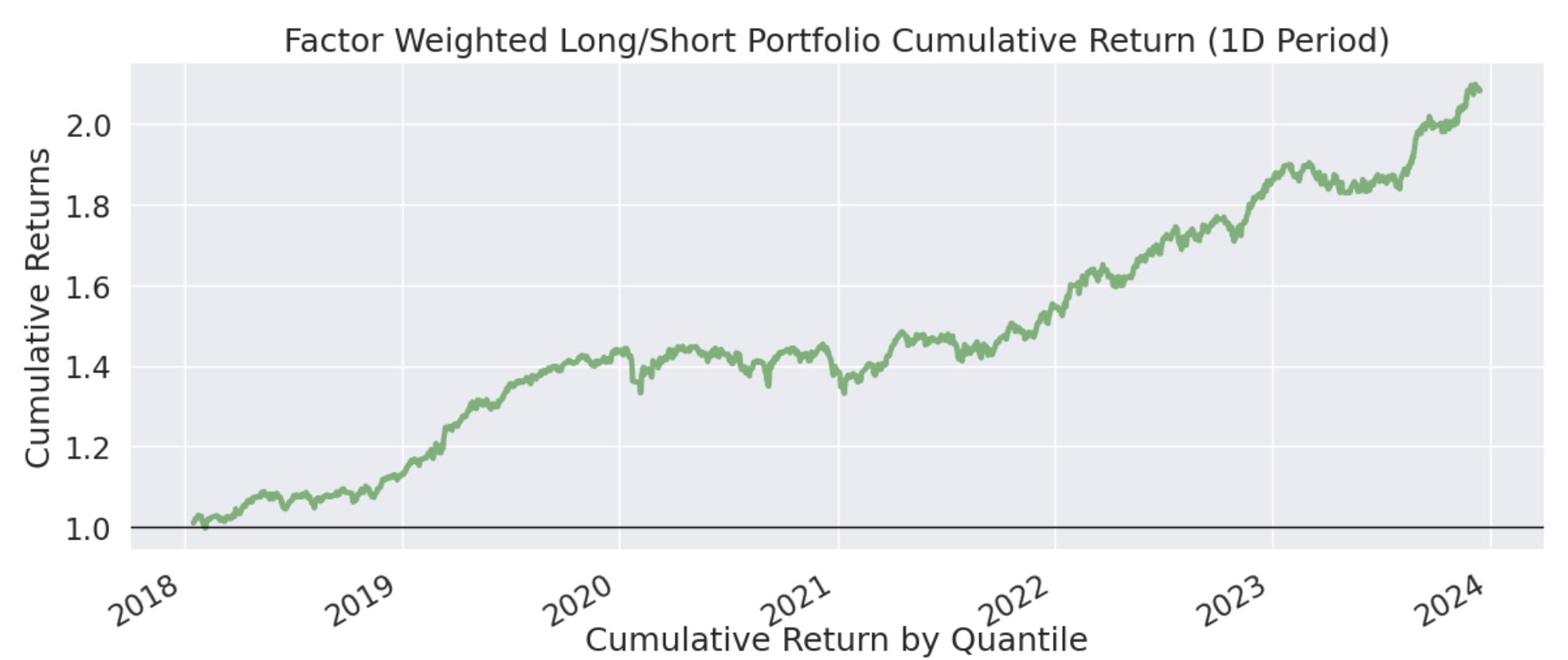 图6 累计收益图
图6 累计收益图
这个收益还没有进行优化。实际上,从下面的分层收益均值图来看,是可以优化的。
 图7 分层收益均值图
图7 分层收益均值图
我们可以在因子检验之前,过滤掉第10层的因子。这样处理之后,我们得到的年化Alpha将达到20.08%,6年累计收益接近3倍。
即使是纯多策略,该因子的年化Alpha也达到了14%。
因子构建及验证代码加入星球后即可获得。

Recurring Phase of Cycle Analysis¶
John Ehler在这篇文章里,提出了寻找周期的方法。
 图8 John Ehlers's Recurring Phase Analysis
图8 John Ehlers's Recurring Phase Analysis
代码使用的是Easy Languange,不过这门语言对我来说一点也不easy。我不知道它是如何实现FFT的,并且还有无处不在的魔术数字。
不过,我完成了一个类似的研究。这个研究旨在揭示fft变换之后的直流分量的意义。
对图1中的时间序列进行fft变换后,去掉直流分量,再逆变换回来,将两者进行对比,我们会得到这样的一个图:
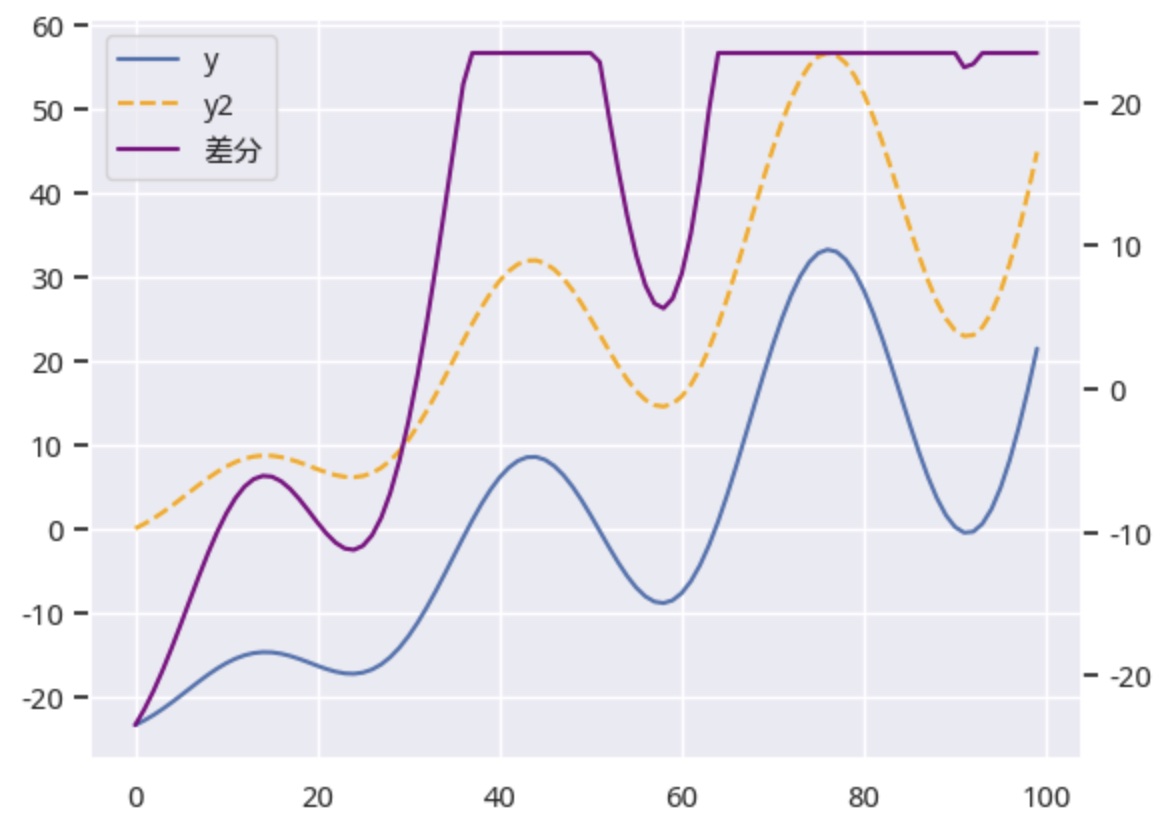 图9 去掉直流分量的对比
图9 去掉直流分量的对比
非常有意思。
第一点,橙色的线是去掉直流分量后的序列(的实部)。它与原序列之间的差值是一个常数,这个常数竟然是原序列的均值!
1 | |
这就是直流分量的真实含义。从数学上讲是一个均值,从交易上讲,它是公司的定价,一切波动都在围绕它发生。
第二点,y与y2的模的差分有上下界。当股价上涨到一定程度之后,一部分能量被浪费在虚部的方向上,该方向是与实部正交的方向,从而导致这个差分有上下界。这似乎是图8中,John Ehler要揭示的信息。
如果一个函数有上下界,它对交易的帮助就太大了。