跳转至

周一到周五，哪天能买股？做对了夏普22.5！

在第12课我们讲了如何从量、价、时、空四个维度来拓展因子（或者策略）。在时间维度上，我们指出从周一到周五，不同的时间点买入，收益是不一样的。这篇文章我们就来揭示下，究竟哪一天买入收益更高。

问题定义如下：

假设我们分别在周一、周二，...，周五以收盘价买入，持有1, 2, 3, 4, 5天，并以收盘价卖出，求平均收益、累积收益和夏普率。我们选择更有代表性的中证1000指数作为标的。

获取行情数据

1
2
3
4
5
6
7
df = pro.index_daily(**{
    "ts_code": "000852.SH"
})

df.index = pd.to_datetime(df.trade_date)
df.sort_index(ascending=True, inplace=True)
df.tail(10)

我们得到的数据将会是从2005年1月4日，到最近的一个交易日为止。在2024年11月间，这将得到约4800条记录。

我们先看一下它的总体走势：

1
df.close.plot()

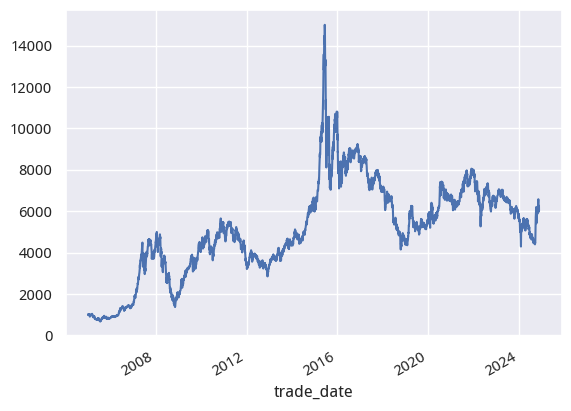
如果我们从2005年1月4日买入并持有的话，19年间大约是得到5倍的收益。记住这个数字。

计算分组收益

接下来我们计算不同日期买入并持有不同period的收益。这里实际上有一个简单的算法，就是我们先按持有期period计算每天的对应收益，然后再按weekday进行分组，就得到了结果。

我们先给df增加分组标志：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
# 给df增加一列，作为分组标志
df["weekday"] = df.index.map(lambda x: x.weekday())

# 将数字转换为更易阅读的周几
df["weekday"] = df.weekday.map({
    0: "周一",
    1: "周二",
    2: "周三",
    3: "周四",
    4: "周五"
})
df = df[["close", "weekday"]]
df.tail()

此时我们会得到：

close weekday
trade_date
2024-11-11 6579.0054 周一
2024-11-12 6491.9723 周二
2024-11-13 6474.3941 周三
2024-11-14 6272.1911 周四
2024-11-15 6125.5126 周五
2024-11-18 5974.5576 周一
2024-11-19 6130.2848 周二
2024-11-20 6250.8029 周三
2024-11-21 6262.1644 周四
2024-11-22 6030.4882 周五

接下来我们计算每期的收益。

1
2
3
4
for period in range(1, 6):
    df[f"{period}D"] = df.close.pct_change(period).shift(-period)

df.tail(10)

此时我们会得到：

close weekday 1D 2D 3D 4D 5D
trade_date
2024-11-11 6579.0054 周一 -0.013229 -0.015901 -0.046635 -0.068930 -0.091875
2024-11-12 6491.9723 周二 -0.002708 -0.033854 -0.056448 -0.079701 -0.055713
2024-11-13 6474.3941 周三 -0.031231 -0.053886 -0.077202 -0.053149 -0.034535
2024-11-14 6272.1911 周四 -0.023386 -0.047453 -0.022625 -0.003410 -0.001599
2024-11-15 6125.5126 周五 -0.024644 0.000779 0.020454 0.022309 -0.015513
2024-11-18 5974.5576 周一 0.026065 0.046237 0.048139 0.009361 NaN
2024-11-19 6130.2848 周二 0.019659 0.021513 -0.016279 NaN NaN
2024-11-20 6250.8029 周三 0.001818 -0.035246 NaN NaN NaN
2024-11-21 6262.1644 周四 -0.036996 NaN NaN NaN NaN
2024-11-22 6030.4882 周五 NaN NaN NaN NaN NaN

现在，我们来计算不同时间点买入时的累积收益率：

1
2
3
4
5
def cum_weekday_returns(df, period):
    return ((1 + df[f"{period}D"]).cumprod() - 1).reset_index(drop=True)

returns_1d = df.groupby('weekday').apply(lambda x: cum_weekday_returns(x, 1))
returns_1d.swaplevel().unstack().plot()

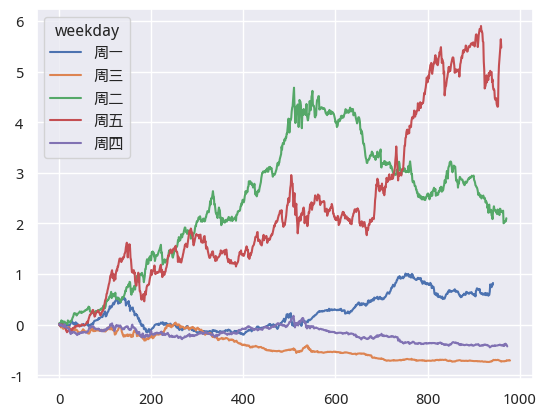
从累积收益图中我们可以看到，周五买入的收益最高，约为5.47倍。看起来这个结果只比买入并持有略好一点，但实际上，资金占有率只有买入并持有的20%。因此，如果算年化Alpha的话，它要比买入并持有高许多。

当然，我们有更好的指标来评估周五买入策略的效果，即夏普率。我们先来看每天交易的夏普率：

1
2
from empyrical import sharpe_ratio
sharpe_ratio(df.close.pct_change())

我们得到的结果是0.46。下面我们计算从周一到周五，不同时间点买入的夏普率：

1
2
3
4
for tm in ("周一", "周二", "周三", "周四", "周五"):
    returns = returns_1d.swaplevel().unstack()[tm]

    print(tm, f"{sharpe_ratio(returns):.1f}")

从结果中看，周二买入的夏普甚至更高。但周三和周四买入的夏普率都为负，这解释了为什么每日买入的夏普率不高的原因。

终极boss

上面我们仅仅介绍了周五买入，持有一天的收益。考虑到周一、周二买入的夏普都很高，显然，如果周五买入，并持有多天，有可能收益会更高。具体应该持有几天会更好，收益会高多少呢？可能会超出你的想像！

你可能读了很多文章，花了很多时间尝试复现它，最终却一无所获：要么代码不完整、要么数据拿不到，或者文章根本就是错的。但我们不想给你带来这样负面的体验。跟本号的其它文章一样，这篇文章的结论是可复现的，并且使用的数据你一样可以获得。你可以加入尝试加入我的星球，通过Quantide Research平台运行和验证本文。如果证实了它的效果，再把代码拷贝到本地，加入你的择时策略中。如果效果不能验证，你也可以退出星球。

1
2
3
4
5
6
def cum_weekday_returns(df, period):
    return ((1 + df[f"{period}D"]).cumprod() - 1).reset_index(drop=True)

for period in range(1, 6):
    returns = df.groupby('weekday').apply(lambda x: cum_weekday_returns(x, period))
    returns.swaplevel().unstack().plot(title=f"持有{period}天")