投资组合理论与实战(1) - 基本概念
现代投资组合理论(MPT)是由马科维茨于 1952 年提出的,是现代金融 7 个基本理论之一。它用数学术语描述了多元化和风险管理等概念,为投资者提供了构建多元化投资组合的工具集,即假定投资者投资于多个资产,在满足给定预期回报率下,可以通过优化求解出风险最小的投资组合。
所有的这些资产组合构成一条曲线(以资产组合的标准差为横轴,预期回报率为纵轴),称为前沿资产组合曲线,其中曲线的上半部分又被称为有效前沿。
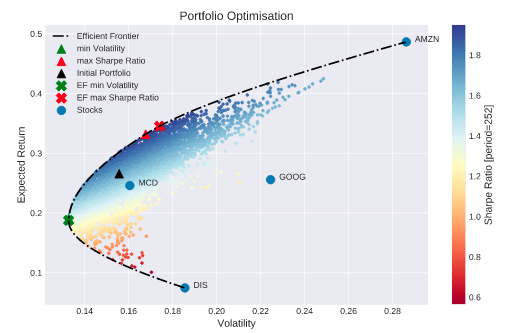
这个图是一个上下对称图,在图的下半部分上的每一个点,都可以在上半部分找到一个对应点,它们具有相同的风险,但有效前沿上的点具有更大的预期收益率。因此下半部分投资是没有投资者愿意持有的。
每个投资者根据自己的风险承受能力(效用函数),在有效前沿上选择自己的投资组合。
马科维茨也因为对 MPT 理论的贡献,从而获得了 1990 年诺贝尔经济学奖。他本人非常看好通过资产组合来分散投资风险这一理念,认为“资产组合是投资中惟一免费可得的午餐”。
基本概念
我们以最简单的两个风险资产组合为例来解释有效前沿:
\[
R_p = w_1R_1 + (1-w_1)R_2
\]
这里:
\(R_p\) 是组合的收益
\(W_1\) 是资产 1 的配比权重
\(R_1\) 是资产 1 的收益。
组合的风险用方差来衡量:
\[
\sigma_p = \sqrt{w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2Cov(R_1, R_2)}\newline
=\sqrt{w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\rho_{1,2}\sigma_1\sigma_2}
\]
这里的\(\rho_{1,2}\) 是资产 1 与资产 2 之间的相关系数。
当两个资产的相关系数为 1 时,上式就化简为:
\[
\sigma_p =\sqrt{w_1^2\sigma_1^2 + w_2^2\sigma_2^2 + 2w_1w_2\sigma_1\sigma_2}\newline
=\sqrt{(w_1\sigma_1 + w_2\sigma_2)^2}\newline
= w_1\sigma_1 + w_2\sigma_2
\]
当两个资产之间的相关系数为-1 时,
\[
\sigma_p =\sqrt{w_1^2\sigma_1^2 + w_2^2\sigma_2^2 - 2w_1w_2\sigma_1\sigma_2}\newline
=\sqrt{(w_1\sigma_1 - w_2\sigma_2)^2}\newline
= w_1\sigma_1 - w_2\sigma_2
\]
从上式可以看出,如果两个资产完全负相关,那么等权重配置两个资产,则资产收益变为零,从而构成一个无风险的组合。此时由于 \(\sigma_p\)等于零,所以它就成为图形上最左端的点。
当其中一个资产为 100%时,则构成图形中上下两个点。
在这个系列中,我们将首先用 4 个标的的组合,先后用蒙特卡洛方法和优化算法分别演示如何求得最佳资产组合,这是比较底层的方法,当我们掌握原理之后,则可以使用第三方库来完成这项工作。
收益率、夏普和波动率计算
让我们首先任意分配一组权重,看看这样得到的组合的收益率、夏普率等各项参数如何。在这个过程中,我们主要是了解:
- 如何获取数据
- 如何产生随机权重向量(重点是满足权重和为 1 的约束条件)
- 如何计算夏普率、波动率等指标。
假定我们的资产组合是:
| 600519 贵州茅台
300750 宁德时代
300059 东方财富
601398 工商银行
|
我们通过下面的代码获得它们近一年的收益,保存在 returns dataframe 中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 | import arrow
import akshare as ak
import pandas as pd
import numpy as np
from IPython.display import display
stocks = ["600519", "300750", "300059", "601398"]
frames = {}
now = arrow.now()
start = now.shift(years = -1)
end = now.format("YYYYMMDD")
start = start.format("YYYYMMDD")
for code in stocks:
bars = ak.stock_zh_a_hist(symbol=code,
period="daily",
start_date=start,
end_date=end,
adjust="qfq")
bars.index = pd.to_datetime(bars["日期"])
frames[code] = bars["收盘"]
prices = pd.DataFrame(frames)
returns = prices.pct_change()
returns.dropna(how='any', inplace=True)
display(returns.head().style.format('{:,.2%}'))
|
这段代码我们在前一篇文章讲 CAPM 时已经见过了。
接下来,我们先随机分配一个权重(这是蒙特卡洛方法的第一步),计算出它的夏普率:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | import numpy as np
from empyrical import sharpe_ratio
weights = np.array(np.random.random(4))
print('Random Weights:')
print(weights)
print('\nRebalance')
weights = weights/np.sum(weights)
print(weights)
# 生成每日每个标的对组合的贡献
weighted_returns = weights * returns
weighted_returns.head()
# 把每一行按列加总,就得到了每日资产收益
port_returns = weighted_returns.sum(axis=1)
# 然后计算组合资产的波动
cov = np.cov(port_returns.T)
port_vol = np.sqrt(np.dot(np.dot(weights, cov), weights.T)) # 0.01
# 使用 sharpe_ratio来计算夏普率
sr = sharpe_ratio(port_returns) # 0.18
print("Sharpe Ratio and Vol")
print(f"{sr:.2f} {port_vol:.2f}")
|
在代码中,我们先是随机生成了一个权重矩阵,然后对它进行了归一化(权重矩阵各项之和必须为 1)。
一些文章会使用对数收益率。但是,在计算方差时,多数人倾向于几何方差是没有意义的(从 google 搜索结果看)。
我们使用了 empyrical 中的 sharpe_ratio 方法来计算夏普率,为简单起见,我们将 risk_free 利率设置为 0。 empyrical 是用来计算策略各项指标,如夏普率、sortino、maxdrawdown 等指标的工具,由 quantpian 开发并开源。像这样的常用量化库,在大富翁量代交易课程中都有介绍。
最终,我们得到以下结果:
| Random Weights:
[0.48349071 0.32903015 0.85308562 0.64038565]
Rebalance
[0.20966711 0.14268485 0.36994299 0.27770505]
Sharpe Ratio and Vol
0.72 0.01
|
最终我们得到了该资产组合的夏普率为 0.72。一般认为,如果我们投资的是指数或者权重股,那么夏普超过 1 是可以接受的投资;对其它高风险权益类投资,一般要超过 1.8,但很少有资产能超过 3。在大富翁量化交易课程里,我们通过蒙特卡洛方法讨论了夏普率与最大回撤之间的关系,即夏普率为 1 时,对应的最大回撤为多少是可能出现的;夏普率为 2 时,对应的最大回撤为多少是可能出现的,等等。
一切准备工作都已就绪,接下来我们将介绍如何使用蒙特卡洛方法来求得上述资产组合的最优配置。
