投资组合理论与实战(4) - PyportfolioOpt工具库

---

Table of Content

这里，我们就介绍一个比较重要的专门用于资产组合优化的工具库。注意，我们已经介绍了 scipy.optimize 库，除此之外，类似的库还有 cvxopt 和 cvxpy。但是，这些库都是比较底层的库，它们主要用于提供各种凸优化算法，不仅仅用于投资领域。

Pyportfolio 则是一个专门用于资产组合优化的库。这个库最初由 Robert Martin 开发。他是一名交易员，Python 爱好者和天体物理学家。这个库在 github 上获得了接近 4k 的 stars。

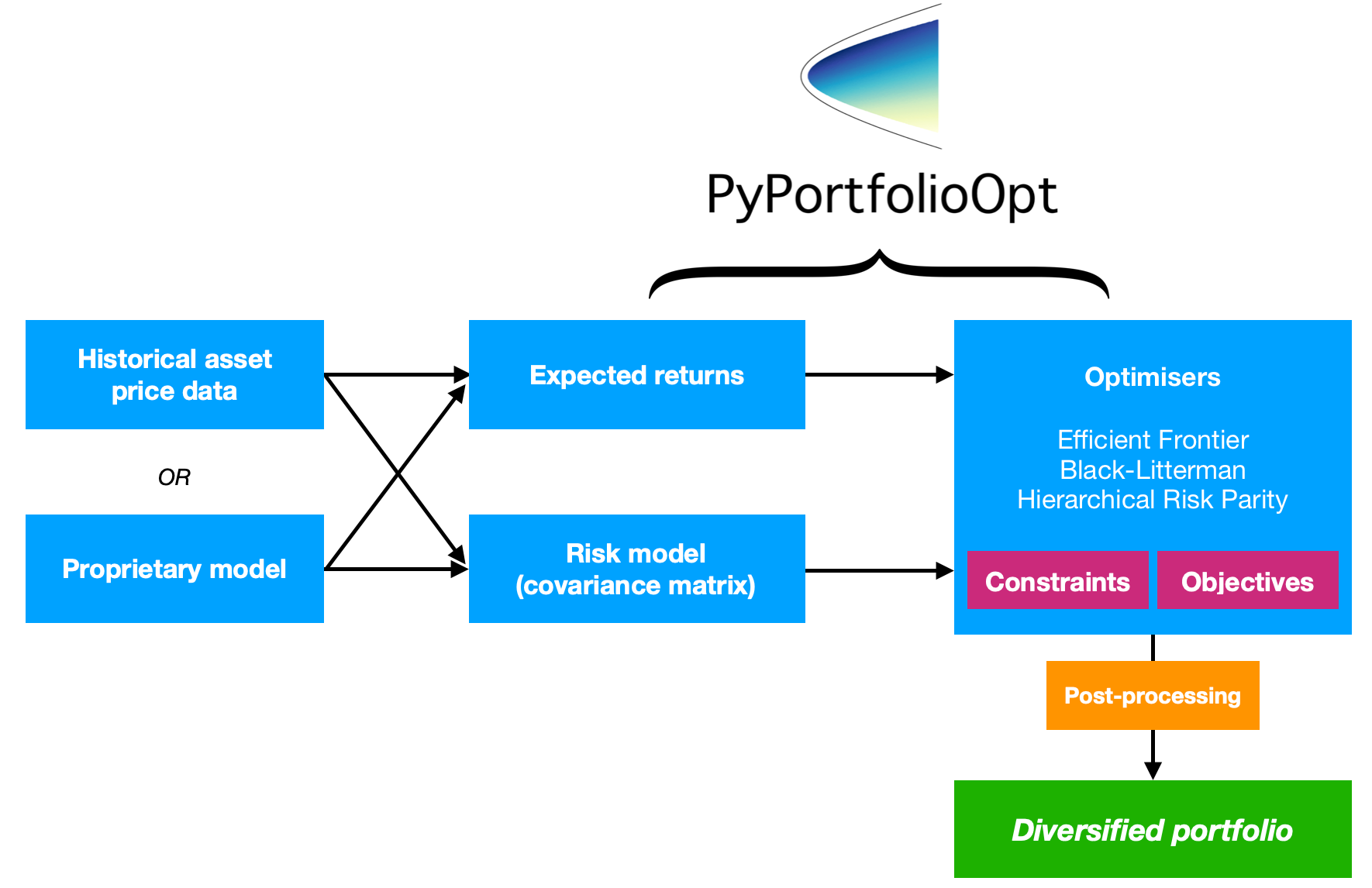
Pyportfolio 提供了以下功能：

1. 多种期望回报模型。比如，在我们前面的方法中，我们使用的 returns 计算方法比较简单，可以称之为平均历史回报。我们在之前的系列中，介绍了 CAPM，这也是一种回报率。pyportfolioopt 工具库除了提供平均历史回报、指数加权平均历史回报之外，它还支持 CAPM 回报。CAPM 与 MPT 双剑合壁，能产生什么样的化学反应，大家也可以在自己的投资中，轻仓尝试一下。

2. 在风险模型方面，之前主要介绍了协方差模型。而 pyportfolioopt 还支持半协方差（Semicovariance，以更关注下行变化的风险度量，呼应我们第 2 个需求）、指数协方差（为最近的数据赋予更多的权重）以及协方差收缩技术

3. 在目标函数上，pyportfolioopt 还提供了最大夏普率 (Maximum Sharpe Ratio)、最小波动率（前面的例子已介绍）、最大二次效用（Maximum quadratic utility）等。
4. 允许持有空头头寸。

以上这些变种组合起来，就为我们拓展 MPT 的应用提供了很多花样玩法。也许，其中就会有一款，正好适合当下的市场。除了这些优化方法外，还有一些常用功能也是我们非常需要的：

1. 可视化。显然，我们需要绘制协方差矩阵、有效前沿、权重矩阵（这是使用饼图的恰当地方，因为权重之和刚好为 1）。
2. 数据预处理，以及后处理。

在了解了 PyportfolioOpt 的基本特性之后，我们再来看看如何使用它。

当前的版本是是 1.5.4，尽管它的基本架构已经稳定，但维护还是很活跃，并且支持从 3.8 到 3.12 的各个版本的 Python。它已经使用了 Poetry 来进行依赖管理。

安装PyportfolioOpt请使用以下命令：

pip install PyPortfolioOpt

它还提供了一个 Docker 容器（真的很贴心了！），供我们练习它提供的一些示例。

接下来，我们将通过一个示例来演示 pyPortforlioOpt的用法。在这个示例中，我们将演示： 1. 如何将数据处理成 PyPortfolioOpt 需要的输入格式 2. 计算协方差矩阵、以及可视化 3. 优化一个多空组合，使得方差最小化 4. 最大化夏普率

数据预处理

我们以使用 zillionare-omicron为例来获取初始数据，并将其处理为 PyPortfolioOpt 需要的输入格式。

Tip

推荐在大富翁量化交易课程课件环境中运行本示例。

from coursea import *

await init()

# 上证50指数
SH50_CODE_LIST = ["688599.XSHG","688111.XSHG","603986.XSHG","603799.XSHG","603501.XSHG","603288.XSHG",
                  "603260.XSHG","603259.XSHG","601919.XSHG","601899.XSHG","601888.XSHG","601857.XSHG",
                  "601728.XSHG","601669.XSHG","601668.XSHG","601633.XSHG","601628.XSHG","601398.XSHG",
                  "601390.XSHG","601318.XSHG","601288.XSHG","601225.XSHG","601166.XSHG","601088.XSHG",
                  "601066.XSHG","601012.XSHG","600905.XSHG","600900.XSHG","600893.XSHG","600887.XSHG",
                  "600809.XSHG","600745.XSHG","600690.XSHG","600519.XSHG","600438.XSHG","600436.XSHG",
                  "600406.XSHG","600309.XSHG","600276.XSHG","600196.XSHG","600111.XSHG","600104.XSHG",
                  "600089.XSHG","600050.XSHG","600048.XSHG","600036.XSHG","600031.XSHG","600030.XSHG",
                  "600028.XSHG","600010.XSHG"]

async def get_prices(stock_list, start_date, end_date):
    frames = [tf.int2date(f) for f in tf.get_frames(start_date, end_date, FrameType.DAY)]
    dfs = [pd.DataFrame([], index=frames)]
    for code in stock_list:
        bars = await Stock.get_bars_in_range(code, FrameType.DAY, frames[0], frames[-1])
        index = [v.item().date() for v in bars["frame"]]
        dfs.append(pd.DataFrame(bars["close"], columns=[code], index=index))

    return pd.concat(dfs, axis=1)

# 投资组合个数
start = datetime.date(2022, 1, 1)
end = datetime.date(2023, 1, 1)
prices = await get_prices(SH50_CODE_LIST, start, end)
prices.tail()

我们将得到以下结果：

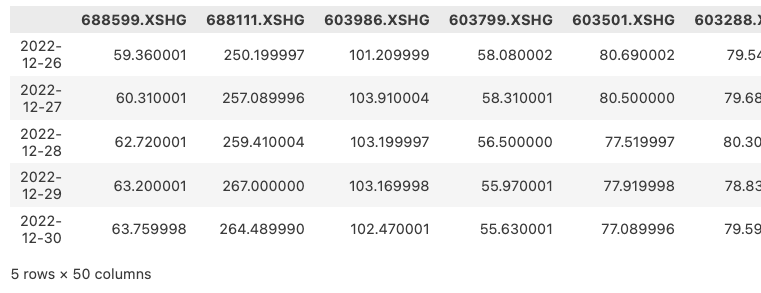
我们将各资产走势绘制成下图：

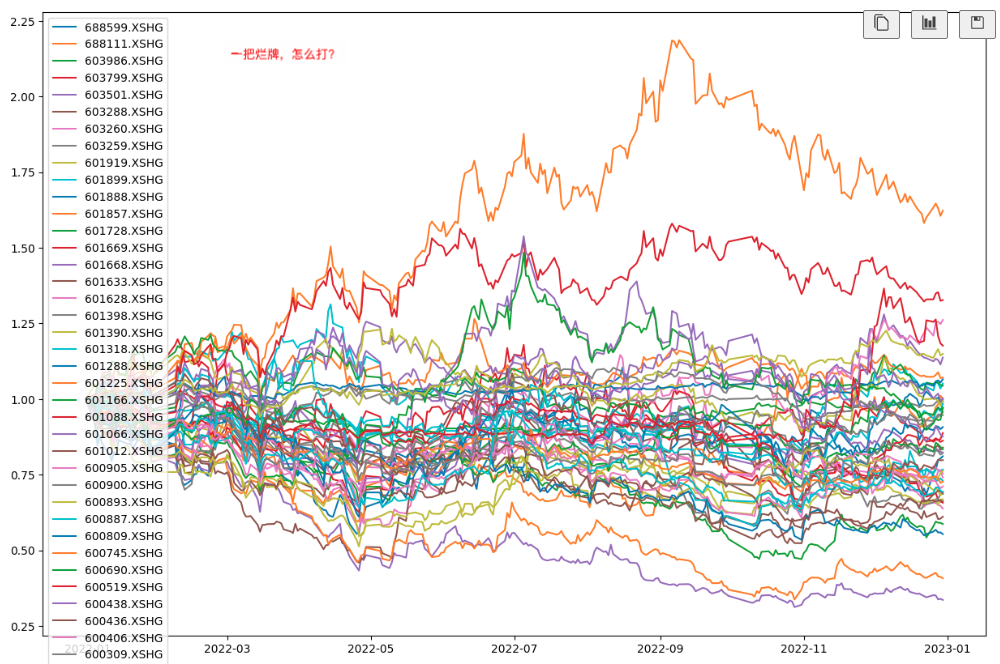
上述代码中，技巧可能在第24行，它将多个dataframe按行进行拼接，最终成为一张宽表。这种格式，在使用pyfolio进行因子分析时，也曾使用过。

计算协方差

在前面的示例中，我们都是手动计算的协方差。在实际工作中，一方面我们可以使用pandas的DataFrame的协方差计算函数cov；在 PyPortfolioOpt 中，我们也可以使用它提供的sample_cov方法：

from pypfopt import risk_models
from pypfopt import plotting

sample_cov = risk_models.sample_cov(prices, frequency=252)
sample_cov.head()

结果如下：

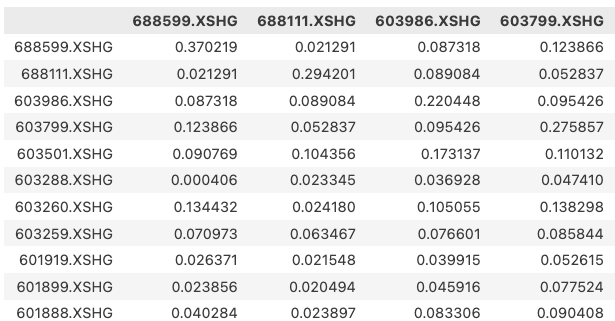
区别在于，如果我们使用PyPortfolioOpt的sample_cov方法，就不需要进行收益率计算和去无效值操作，即一步操作，完成以下功能：

prices = ... # pd.DataFrame, price of each instrument
returns = prices.pct_change().dropna(how='any')
cov = returns.cov()

我们通过以下命令，来可视化该矩阵：

plotting.plot_covariance(sample_cov, plot_correlation=True)

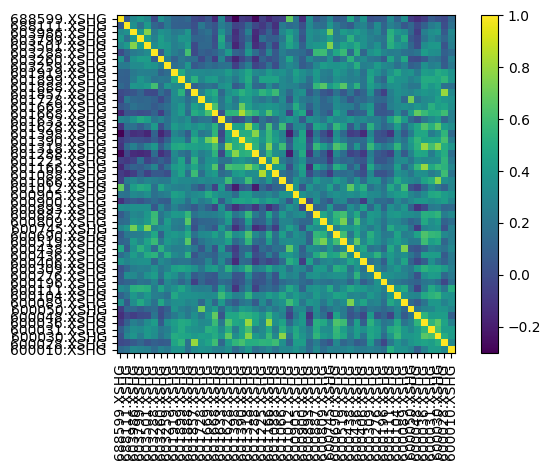
求解最优资产组合

我们以最大收益、最低波动来条件来求解最优资产组合：

from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt.expected_returns import mean_historical_return

mu = mean_historical_return(prices)
S = risk_models.sample_cov(prices)

ef = EfficientFrontier(mu, S, weight_bounds=(0, 1))

# 求解出最小波动率时的权重
w = ef.min_volatility()

# 输出最小波动率时的年化收益、波动率和sharpe
ef.portfolio_performance(verbose=True)
df_w = pd.DataFrame(np.array([item for item in w.items()], dtype=[("code", "O"), ("w", "f4")]))

# 显示权重
df_w.head()

使用方法很简单。首先，我们求得回报均值，构建risk model，这里我们使用的是均值方差模型，因此，通过sampe_cov来返回这个模型。

然后我们在第8行，实例化有效前沿对象。它接收三个参数，即均值、risk model和权重约束）。

然后在第11行，我们以最小波动率为目标进行优化求解，得到的结果即为权重向量（以orderdict类型表示）。我们可以根据这个向量来自行计算对应的组合年化收益、夏普率，但也可以使用 pypfopt 自带的方法 portfolio_performance，如代码第14行所示。

最后，我们将权重向量转换为dataframe进行显示，这纯粹是为了美观。

这样，我们就求得了波动最小时的期望收益、资产组合（即权重），以及它们的夏普等指标。

可视化与有效前沿

我们刚刚使用的方法，仅生成了单个最优投资组合。但很多时候，我们可能还希望获得整个有效前沿。

fig, ax = plt.subplots()
ef = EfficientFrontier(mu, S, weight_bounds=(0, 1))
ef_max_sharpe = ef.deepcopy()
plotting.plot_efficient_frontier(ef, ax=ax, show_assets=False)

# Find the tangency portfolio
ef_max_sharpe.max_sharpe()
ret_tangent, std_tangent, _ = ef_max_sharpe.portfolio_performance()
ax.scatter(std_tangent, ret_tangent, marker="*", s=100, c="r", label="Max Sharpe")

# Generate random portfolios
n_samples = 10000
w = np.random.dirichlet(np.ones(ef.n_assets), n_samples)
rets = w.dot(ef.expected_returns)
stds = np.sqrt(np.diag(w @ ef.cov_matrix @ w.T))
sharpes = rets / stds
ax.scatter(stds, rets, marker=".", c=sharpes, cmap="viridis_r")

# Output
ax.set_title("Efficient Frontier with random portfolios")
ax.legend()
plt.tight_layout()
plt.show()

最终我们会得到下图：

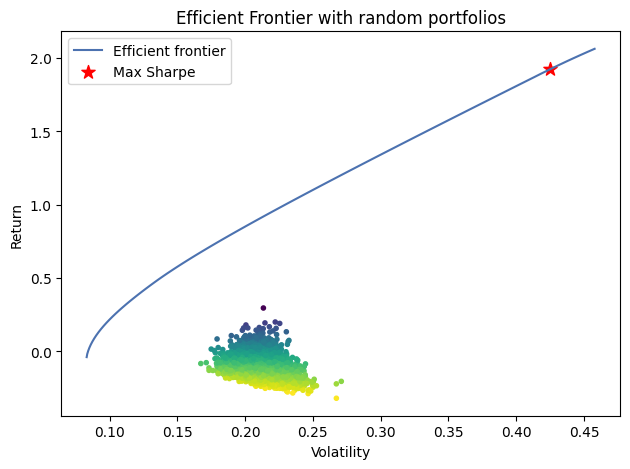
这里有几点需要说明：

1. 我们共生成个两次有效前沿实例。第一个使用的是均值方差模型（即回报与波动率）进行的求解，第二个则是对最优夏普率进行的求解。对任何一个实例，只能进行一次求解，所以，我们生成了两个实例。这里使用的是deepcopy方法，也可以完全重新初始化。

2. 第13行我们使用了狄利克雷分布。它是一个在(0,1)区间内分布，但分布总和为1的分布。我们在之前是使用下面的方法来做到这一点的：

w = np.random.random(size=50)
w = w/sum(w)

使用狄利克雷分布的写法看上去更优雅。不过要注意，两种方法的分布特征是不一样的。

CAPM与MPT

前面一个系列讲解了CAPM。它与MPT有着千丝万缕的联系。首先，我们在求解最佳夏普率时，使用了 tangency portfolio，即切线投资组合这一说法（注释第6行）。切线投资组合是一种位于风险回报空间中有效前沿与最高可能资本市场线 (CML) 相切点的投资组合。

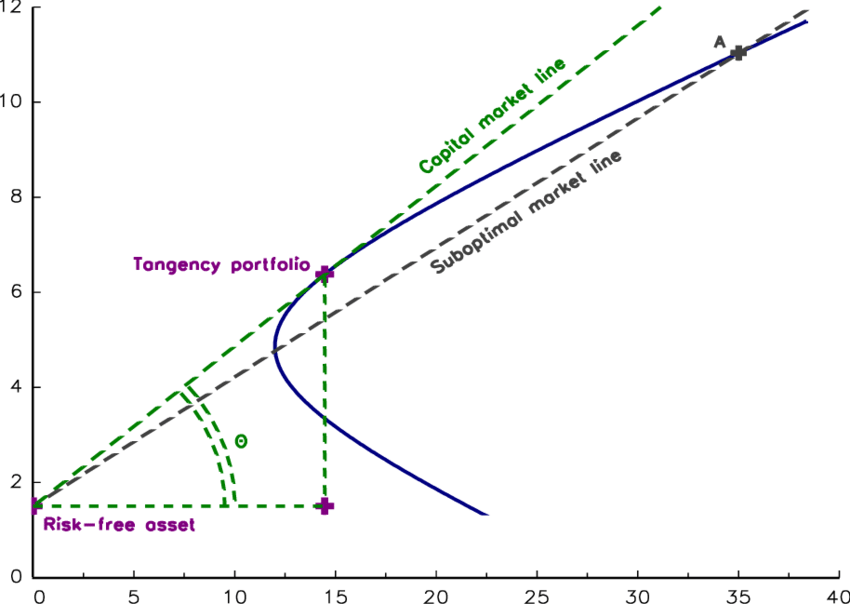
这里的切线的斜率，就是夏普率。

另外，我们在之前的计算中，使用的都是均值回报率，通过mean_historical_return求得。但实际上，均值回报率参考意义并不太大。因为我们不能简单地假设历史会重演。一种可能的办法，是通过CAPM求得资产的alpha，以此作为资产回报再来计算有效前沿。因此，在这一点上，CAPM与MPT理论有机地结合到了一起。

pyfolio支持了这种做法。我们在实例化 EfficientFrontier对象时，可以这样：

from pypfopt.expected_returns import capm_return

# 不用历史回报，而改为capm_return

#mu = mean_historical_return(prices)
mu = capm_return(prices)
S = risk_models.sample_cov(prices)

ef = EfficientFrontier(mu, S, weight_bounds=(0, 1))

不过，在我们的示例中，使用capm return可能会出错，提示没有任何一种资产的CAPM收益为正。这不是pyfolioopt的错，也不是我们的错。

这个市场错了。

结束语

这一系列的理代投资组合理论就介绍到这里。在这个系列中，我们除了掌握了如何运用投资组合理论来实际管理资产之外，我们还学到了蒙特卡洛方法、凸优化方法，掌握了sharpe率的计算等重要的量化工具。我们还介绍了MPT与CAPM是如何连接起来的，如果您对纯理论研究比较感兴趣，可以顺着这部分继续深入研究。我们在参考文献里给出了一些阅读资料。

现代投资组合的理论，以及其它重要的金融学理论，尽管在学术上非常成功（获得了诺奖），但我们也要注意，它们过于精巧的理论架构，往往是脱离实际的，也因而不被在实践中获得伟大成功的那些投资大师所看重 -- 比如查理.芒格就特别看不上有效市场假说和现代投资组合理论。

在穷查理宝典中，他这样写到：

Quote

Beta 系数、现代投资组合理论等等——这些在我看来都没什么道理。我们想要做到的是，用低廉的价格，甚至是合理的价格，来购买那些拥有可持续竞争优势的企业。

大学教授怎么可以散播这种无稽之谈（股价波动是衡量风险的尺度）呢？几十年来，我一直都在等待这种胡言乱语结束。现在这样乱讲的人少了一些，但还是有。

顺便说一声，我给那些信奉极端的有效市场理论的人取了个名字 -- 叫做“神经病”。那是一种逻辑上自洽的理论，让他们能够做出漂亮的数学题。所以我想，这种理论对那些有很高数学才华的人非常有吸引力。可是它的基本假设和现实生活并不相符。

他还提到，这位世界上最伟大的经济学家之一，竟然是伯克希尔·哈撒韦的大股东，自从巴菲特掌管伯克希尔之后不久，他就开始投钱进来。他的教科书总是 教导学生说股市是极其有效率的，没有人能够打败它。但他自己的钱却流进了伯克希尔，这让他发了大财。

尽管如此，学习这些理论，掌握它背后的数学方法、工具和思想，对增强我们的量化基本功，还是非常有必要的。在学习投资的道路上，不存在这样的一个理论和系统，只要你学习了它就能战胜市场。只要你不打算做资本市场里的骗子，一万小时定律就仍然对你适用。从基础入手，构建自己的方法论和洞察市场，才能树立自己的竞争门槛。

这也是大富翁量化交易课程在编撰时秉持的原则。我们不承诺教会你马上可以一招致胜的策略，相反地，我们把市场上流行的量化工具、金融理论一一拆解，还原成一个个高复用的知识点，然后按照量化交易的天然流程重新组织起来，从而使得学员打下坚实的量化基础。

参考文献

Yang (ken) Wu: 使用Python和R进行投资组合优化 Pyportfolio 工具库 Pyportfolio cookbook Investopedia: 了解资本市场线及其计算方法 普林斯顿大学: 均值方差分析及CAPM定价模型 CFA水平测试: The CAL and CML