基于深度学习的量化策略如何实现归一化？

基于深度学习的量化策略如何实现归一化？本文首先辨析了归一化、标准化与正则化三个术语，然后分析了min-max, sin, sigmoid等归一化函数在量化中使用时常犯的错误，讲解了如何制作一个好的归一化函数。最后，以一些量化因子归一化示例作为结束。

归一化、标准化与正则化辨析¶

归一化、标准化与正则化是机器学习/深度学习中相似但又相区别的几个概念。

归一化 (normalization)是指将数据分布映射到[0,1]的区间来。我们可能是在统计学中最初接触到这一概念，主要方法有min-max scaling, 但在深度学习中，常常使用的归一化方法远不止于此，还有tanh, sigmoid, sin等等。min-max归一化的公式是：

\[ X' = \frac{X - min(x)}{max(X) - min(X)} \]

不是所有能实现变量到值域[0,1]之间的映射的函数，都能拿来做归一化函数的。归一化函数必须满足的一个条件就是，它不能改变数据之间的位置关系。比如，如果有自变量\([x_0, x_1]\)，对应的函数是\([y_0, y_1]\),且\(x_0 >= x_1\)的话，那么\(y_0 >= y_1\)也必须得到满足。这个规则，可称单调性原则。出于这个原因，像sin这样的函数很少用在深度学习中（但也不绝对！）。另外，什么才是一个好的归一化函数？我们也将在后面继续讨论。

在实现上，我们可以使用sklearn.preprocessing.MinMaxScaler来进行转换。

标准化 (standardization)一般是指将数据按以下公式进行处理：

\[ z = \frac{X - \mu}{\sigma} \]

即z-score化。进行标准化处理以后，函数z将服从 \(N(0,1)\)的正态分布。在实现上，我们可以使用sklearn.preprocessing.StandardScaler（或者scale()）来处理。

归一化与标准化实际上有较大的区别。实现归一化后，数据集的值域将落在[0,1]（或者在[-1,1]之间。通过归一化处理，不同量纲的物理量实现了去量纲化，从而它们可以在深度学习中，以相同的学习率（learning-rate）来进行梯度优化。但标准化后的数据集，它的值域没有范围限制，因而它仍然是有量纲的。这样不同的因子被标准化后，仍然在量纲上不一致，所以是不能放到一起进行训练的。另外，标准化有意义的前提是，数据集本身要满足正态分布。

正则化则是将标准化后的数据集，除以它的范数，从而数据被缩放到[-1,1]区间内。正则化后的结果消除了量纲，是适用于深度学习的。正则化的公式是

\[ X' = \frac{X}{||X||} \]

在sklearn中，实现方法是sklearn.preprocessing.Normalizer。

如果是机器学习，部分算法，比如decision-tree和boost类的算法，这三种变换都是没有必要做的。因为这些算法与量纲无关。

但在深度学习中，涉及到权重优化的学习率问题，因此各向量（在量化中即为因子）的量纲必须统一，因此，我们必须实现归一化或者正则化。显然，标准化是没有太多意义的。

在深度学习中归一化的方法很多，远不止统计学上的min-max scaler这一种。具体用哪一种，跟我们的的数据分布、要解决的问题是相关的，所以sigmoid, tanh, sin（这个最早在NMT中使用）,min-max等都有使用。

常见的归一化函数讨论¶

min-max scale¶

在基于深度学习的量化策略中，决不能直接使用股价、或者任何它的一阶线性变换来进行min-max scale来作为因子。在很多领域，min-max归一化是有效的，因为这些领域中的数据是有界的。比如，人的身高，大约是20cm到250cm。这是一个确定的上下界。但股票价格只有下界，没有上界。比如万科的股价，以后复权来看，在2018年达到过3700元。如果我们采用2000年以前的股价作为因子，并且进行min-max scale，那么最终的预测值是决不会超过当时的最高价的。

但是涨跌幅、RSI等指标则比较适合进行min-max scale。你应该注意到，它们是股价的二阶函数。

sigmoid和tanh¶

这两个函数效果几乎相同，但在深度学习中，我们使用sigmoid会多一些，因为它在求导时，计算性能更好。

\[ S = \frac{1}{1 + e^{-x}} \]

对sigmoid函数进行求导，其结果为

\[ dS = S * (1 - S) \]

这样在计算中可以利用原函数，所以速度更快。

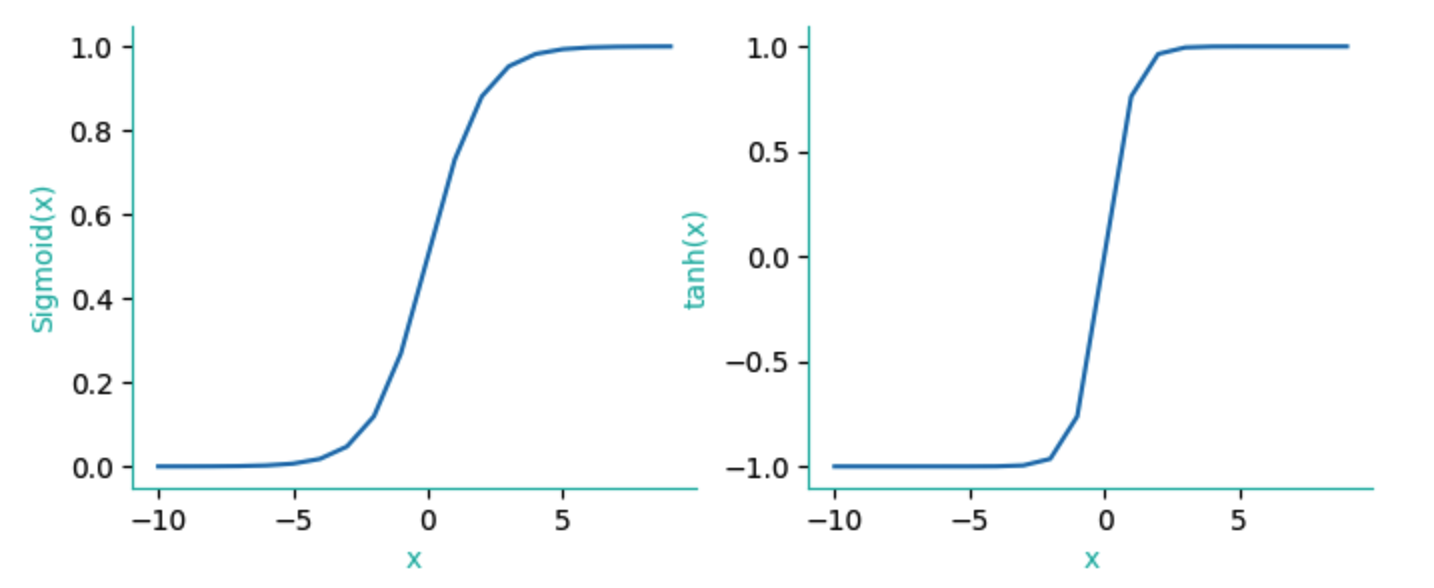
两者的变换图形如下：

50%

sine¶

一般情况下，我们不使用sin函数来进行归一化。因为它的取值有周期性。但这也不绝对，在google早期的NMT模型中，就大量使用了sin来进行归一化，因为它正好能提取两个相关联的语素之间间隔的周期性。尽管很少看到报道量化策略在深度学习上使用sin函数，但考虑到经济的周期性，交易行为的周期性，周期类的归一化函数一定可以在因子提取中发挥作用。

z-score和正则化¶

前面介绍过，z-score方法不能去量纲，因而一般不适用于深度学习。正则化方法能将数据压缩在[0-1]区间，我们要注意的是，跟min-max一样，我们不能直接拿股价变换作为因子。当然这一点，可能对其它方法也是适用的。

有人会认为，股价波动不符合正态分布，这是我们不能使用z-score变换的原因，实际上主要原因还是量纲问题。是否符合正态分布，更多地是意味着我们能否（如何）进行统计推断的问题。另外，不符合正态分布的数据，数据点之间的分布会出现扎堆，不够均匀的问题。

这也引出来归一化函数的评价问题，即什么是好的归一化函数

什么是好的归一化函数¶

在量化策略中，好的归一化函数，首先要满足单调性原则，其次，要使得最常出现的数据点，有最好的响应灵敏度。此外，还涉及到分辨率问题。

要注意的是，有一些函数，在数学上满足单调性，但在计算机实现中，由于浮点数误差问题，会导致实际上不满足单调性。

比如 sigmoid(13) 和sigmoid(26)，哪个大？从数学上看，\(26 > 13\)，因此， \(sigmoid(26) > sigmoid(13)\)成立。但实际上，下面的代码将验证这两个数值是相等的：

import numpy as np

def sigmoid(x):
    return 1/(1 + np.exp(-x))

assert sigmoid(13) - sigmoid(26) < 1e-7

1e-7是32位浮点数所能精确表示的最小精度。而我们在深度学习中，权重矩阵一般使用32 bit，现在16-bit的权重也很常见了。

sigmoid(13)与sigmoid(26)相等！这意味着单调性原则被打破。

另一个问题就是响应灵敏度。我们为什么要对数据进行z-score化?这是为了让出现频率最高的数据段，它们都映射到以0为中心附近的区域上来，在这一区段，响应灵敏度最高。

从sigmoid与tanh的对比图可以看出，对sigmoid而言，在[-5，5]区间内的数值，它的们sigmoid值对x有较好的响应灵敏度，超过这个区间，则出现钝化。这种钝化意味着我们必须使用更小的学习率(learning-rate)才能进行较好的调校。

所以，我们一般不直接使用sigmoid，而是使用它的一个变换版本：

def scaled_sigmoid(x, start, end):
    """当`x`落在`[start,end]`区间时，函数值为[0,1]且在该区间有较好的响应灵敏度
    """
    n = np.abs(start - end)

    score = 2/(1 + np.exp(-np.log(40_000)*(x - start - n)/n + np.log(5e-3)))
    return score/2

下面的图，显示了当数据主要分布在不同的[start, end]区间时，变换后的sigmoid方法都能使得中心分布有最好的响应灵敏度 -- 这也是为什么我们要做z-score变换的原因。

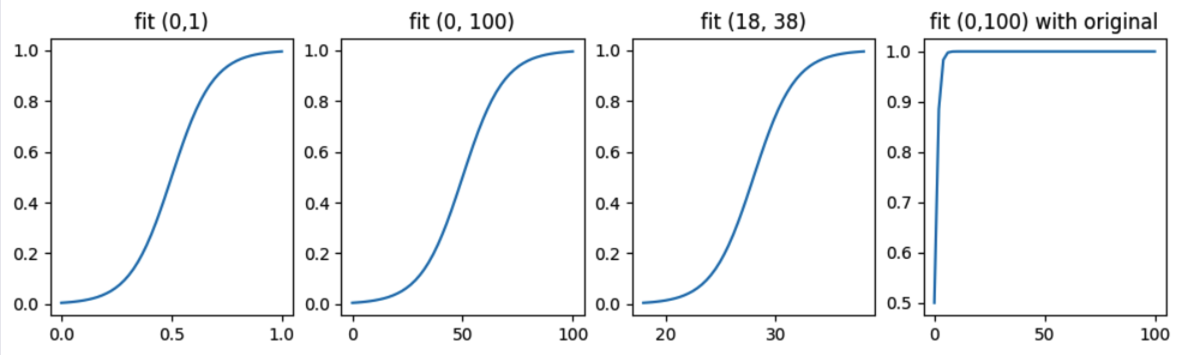
在子图1中，我们让数据在[0,1]之间有最好的响应灵敏度。子图2中，如果数据经常落在50附近，正负50之间波动，也能得到最好的响应灵敏度。子图4则显示的是原始的sigmoid在[0,100]之间的取值情况。

因子归一化示例¶

涨停后整理周期因子¶

股票涨停是强势的表现（你可以自己尝试一下，早盘10：00强涨停的股票，要维持它不打开会有多难）。考虑到涨停当天无法买进，但后续可能调整一段时间，可能有低位进场的机会。我们想知道，大概在涨停后第几天进场，成功率最高。

Tip

在这个例子中，如果纯粹只看时间周期，应该是1, 3, 5, 8等fib序列。10和20也是不错的数字，刚好对应两周和一个月。

这是可以使用sin进行归一化的例子。涨停后的调整天数，本来就没有单调的意义（即，不会调整起久，上涨概率越大），相反，它可能呈现某种周期因素。

地量因子¶

如果某支股票、或者批数某一天见了地量，这意味着人气冷清到极点，下跌也到了尽头。所谓地量见地价。

我们可以用当天的成交量是多少天（n）以来的最小值来描述地量。显然，这个值越大越好。但它也不可能无限大，如果真是这样，地量见地价这一股谚也就不成立了。

我们可以统计一下，然后取一个合理的区间，用上面的scaled_sigmoid来提取因子，用以深度学习。这个区间的下界，可能至少得30起。

概率因子¶

一些数据转换成概率之后，天然就是分布在[0,1]之间的。所以，当我们没有归一化思路时，也可以通过经验分布函数，求得经验cdf/ppf函数，从而得到某个数据出现时，对应的概率。这个概率也可以作为深度学习的因子。

对本文中的一些概念，比如浮点误差，归一化函数的作用，CDF/PPF，不太理解的话，你可能需要系统地学习一些量化课程。本篇内容整理自我们的课程素材，欢迎加入！