Z-score 因子的深入思考

R50

最新（2024 年 1 月）出版的 SC 技术分析（Techical Analysis of Stock & Commodities）的第 4 条文章给到了 Z-score，原文标题为《Z-score: How to use it in Trading》。今天的笔记，就借此机会，同步推出我们对通过Z-score来构建量化因子的一些观点。

Tip

SC 技术分析杂志由波音的机械工程师 Jack Huston 创建于 1982 年，内容涵盖全球行业趋势、杰出人物、交易技术、管理基金以及基本面和技术分析，目前有 1 百多万订阅者，是当下量化交易者必读的杂志之一。

题外话，在过去，技术分析大师往往是机械工程出身，比如发明 RSI,ATR 和 SAR 等经典技术指标的 Welles Wilder 也是一名机械工程师。在未来，交易中的杰出人物则可能来自软件行业。

Z-Score 的计算¶

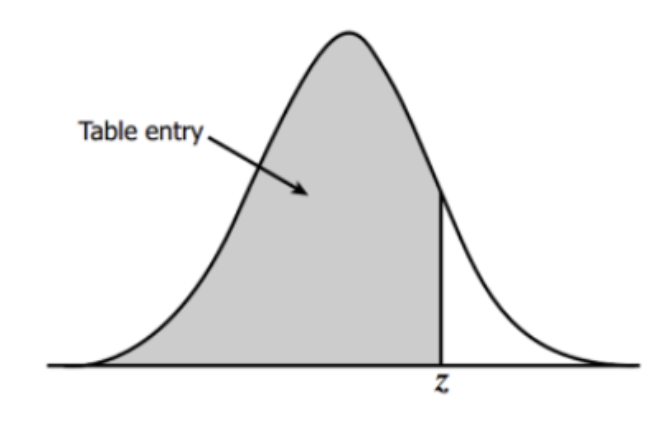
Z-score 的计算公式如下： $$ Z = \frac{X-\mu}{\sigma} $$

这里$Z$是 z-score，$X$一般取股价，$\mu$是均值，$\sigma$是标准差，也称波动率。

如果 X服从正态分布，那么将有以下结论： 1. abs(z-score) >= 2 的概率小于 2.3% 2. abs(z-score) >= 3 的概率小于 0.13%

由此可以作为某种反转信号，即一旦z-score超过±2，将有97.7%的概率会回归到±2 以内，也就是股价会发生向均值方向的回归。

在 scipy.stats 包中有 zscore 计算函数，但它是基于我们传入的全部数据的。在因子构建中，我们实际上要计算的是rolling-zscore。因此，我们借用 pandas 中的 rolling 方法来自行计算：

def rolling_zscore(s, win=20):
    ma = s.rolling(window=win).mean()
    std = s.rolling(window=win).std()
    return (s - ma)/std

Info

在 numpy 中没有 rolling 这个方法，它在 np.lib.stride_tricks 中，提供了一个 as_stride 方法来提供滑动窗口数据。但是出于性能的考虑，numpy 并不推荐使用这个方法。在 pandas 中，rolling 方法有其 cython 及 numba 的实现，速度上更占优势。
这一局， pandas 胜。

因子检验¶

这篇笔记不打算走完整的流程，我们将随机选择一个标的，计算它最近 250 期的 zscore，把 zscore 小于-2 的点作为买入点，大于 2 的点作为卖出点，进行绘图显示，然后就图的走势，来进行深入讨论：

可以看出，每一个买入点差不多都是局部的最低点，每一个卖出点也差不多是局部最高点。但是，在下跌趋势中，即使我们在最低点进入了，它的反弹并不能持续多久（或者多大的幅度），而且很难等到 zscore 的卖出点，往往就已经拐头了。

或者说，zscore大于2，是一个卖出的充分但不必要条件；zscore 小于-2, 是一个买入的充分但不必要的条件。它不对未来趋势进行预测，并且在 97.7%的时间里，不会发出交易信号，这样资金利用率也不够。因此，zscore 可以构成一个因子，但不能构成一个策略。但作为因子，它仍然是优秀的，因为它能发出确定、胜率很高的信号。

与布林带的关系¶

如果你熟悉布林带策略，那么你会发现，z-score 的算法与布林带一模一样。不同的是，布林带的上下轨的数值是均值的±2个标准差，取值的波动可以很大，而z-score的取值是在确定的范围内（-3, +3），具有类似归一化的特征。正因为如此，它可以很方便地当成因子，用在机器学习中。实际上，要做到真正的归一化，我们直接取 z-score 的累积概率就好，它是在 [0,1] 区间分布的，并且当 z-score 为 2 时，累积概率为 0.977.

Info

布林带是上世纪 80 年代风靡一时的策略。它甚至被注册为商标，我们今天在英文世界里引用这个词，都要使用 Bollinger Bands^®这个表示方法。为什么布林带曾经大赚特赚，而现在效果一般般呢？这实际上是一个行为金融学方面的话题。在 80 年代，这个指标刚出来时，以其不可辩驳的统计学原理，一下子征服了很多人，信仰的力量改变了大家的交易行为，从而使得交易者陷入自我预言实现的魔咒里。

警惕黑天鹅¶

与其它别的因子不一样的地方是，z-score 因子的有效性来源于正态分布的假设。只有股价的波动符合正态分布，我们才能断言价格偏离均值加两个标准差的可能性小于 2.3%。然而，股价的波动并不符合正态分布（指数会更接近一点，但也是更符合广义双曲分布，而不是正态分布）。因此，z-score因子（以及布林带）的理论根基并不牢固。

另外，最重要的一点是，在偏离两个标准差的地方，尽管其概率很小，但也存在一种可能，就是它一旦发生，其后果会比较严重。这就是由 Taleb 提出的所谓黑天鹅效应。在 A 股中，需要注意的是，如果在偏离两个标准差的地方，如果发生了涨跌停，那么我们应该果断放弃 z-score 因子。因为在这种情况下，交易情绪是极端化的。

Quiz¶

如果价格的波动并不服从正态分布，或者任何一种已知的分布，我们又该如何把握它的统计学特征呢？

举例来说，如果有这样一个问题，今天沪指已经下跌了4%，依据过去1000个交易日的统计数据，它继续下跌的概率是多少，你应该如何回答这个问题？能够正确地回答这个问题的人，才能抓住加速赶底、或者因意外事件错误下跌的机会。

提示：这是我们在课程中，用来引出PDF/CDF概念的一个问题。

Tip

Z-score与布林带一样，都是以正态分布原理为基础，通过均值与标准差的关系，确定波动的“不合理”区间，并期望发生向均值的回归。
Z-score是一个居于(-3,3)间的数值，其中超出±2的概率为2.3%。
Z-score在数学上很完美，但股价的波动并不符合正态分布，也就是其理论基础并不坚实。许多现代金融理论只能在无法满足的条件上运行，这也是查理.芒格嘲笑经济学家的地方。

本文所附源代码