Alphalens因子分析(2) - low turnover秒杀98%的基金经理!

上一篇笔记，我们已经为因子分析准备好了数据。这一篇笔记，我们就进行因子分析。分析过程在 Alphalens 中非常简单，核心是读懂它的报告。

Alphalens 框架

Alphalens 的主要模块是 utils, tears, performance 和 plotting。

utils 主要功能是提供数据预处理，我们已经在上一篇笔记中，已经使用过 get_clean_factor_and_forward_returns 这个方法，实际上是由quantize_factor get_clean_factor和compute_forward_return 这样三个方法构成的。

---

在这个方法运行时，它会输出这样的提示信息：

Dropped 4.1% entries from factor data: 4.1% in forward returns computation and 0.0% in binning phase (set max_loss=0 to see potentially suppressed Exceptions).

max_loss is 35.0%, not exceeded: OK!

它涉及到因子分析框架的几个步骤，在我们的课程中，对其原理有详细讲解。作为一个快速入门，我们就跳过这些细节。我们只要知道，看到最后的 not exceeded: OK！就大功告成。

为什么需要掌握因子分析的原理？

在我们这个简单（但这个因子仍然有效）的示例中，因子构建过程会运行得很丝滑。但一旦你开始构建复杂的因子，就会遇到各种问题。这其中最常见的，可能就是分组平衡、缺失值处理后，有效记录不足等等，就会卡在这一步。

这张导图显示了Alphalens的模块组织情况:

---

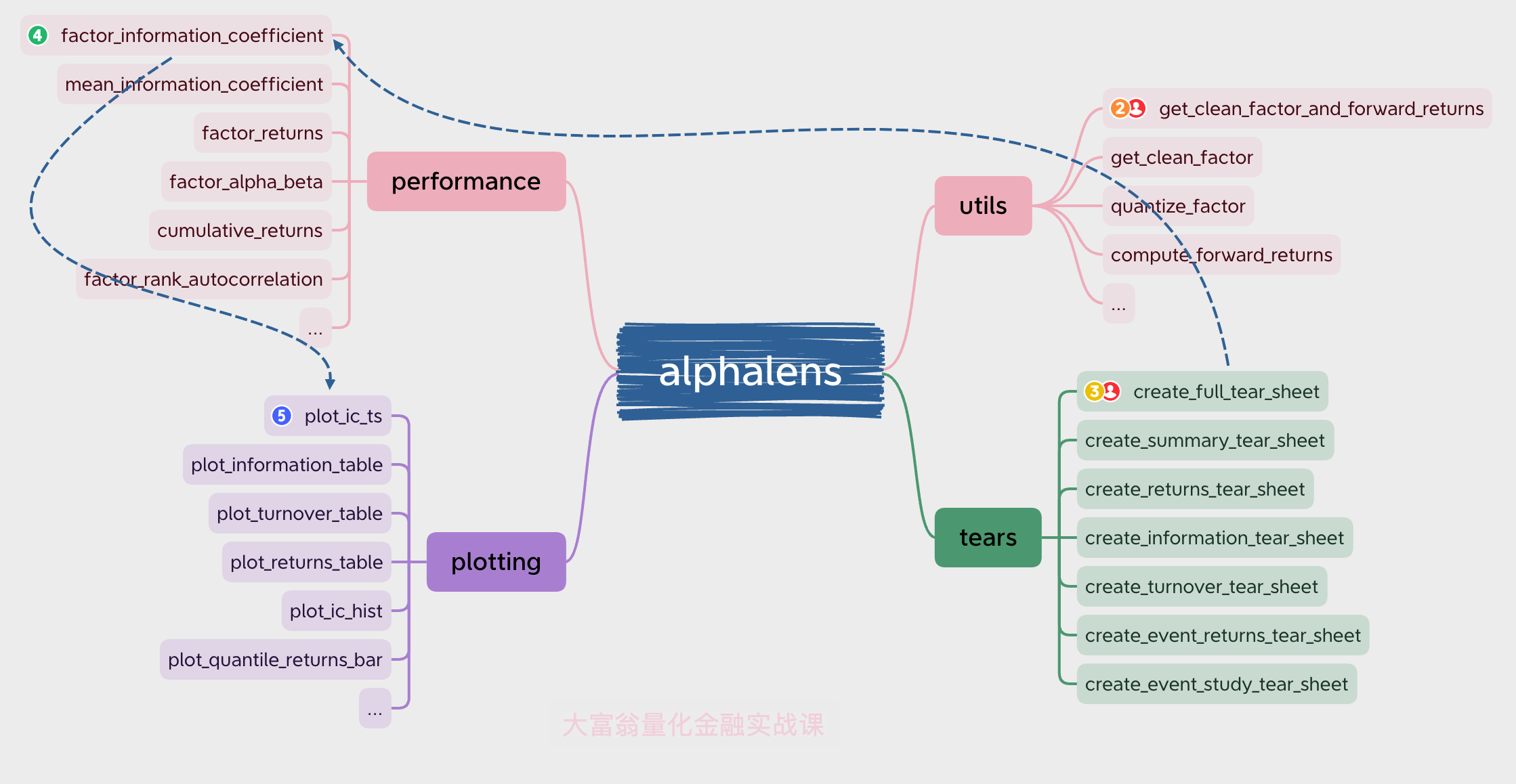
performance 模块提供因子分析的基础功能，plotting 模块提供图形绘制功能。而 tears 模块则是将 performance 与 plotting 的操作组合起来，向用户生成报告。

utils 与 tears 模块是用户接口，我们可以只使用这两个模块中的功能，而不去管 performance 与 plotting 模块具体是怎么工作的。

现在，我们来查看 factor_data（请回顾上一篇笔记，以了解这个数据是如何生成的）:

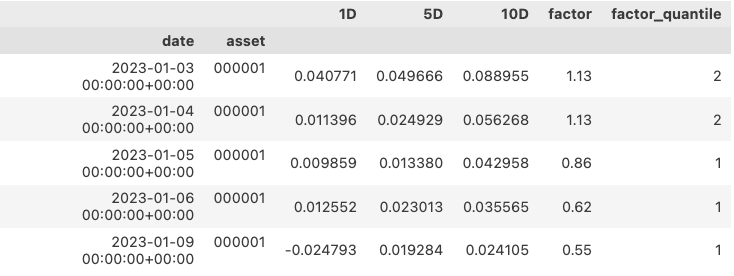
列"1D"等代表了对应行所属的时间戳之后的 N 天的收益。factor 则是当时的因子值，factor_quantile 则是该因子在当天中的分层。因此，第一行记录表明，对于 000001 这个标的，在 1 月 3 日，因子为 1.13，属于第二组（由小到大，从 1 开始）。该资产在随后的一天、五天和十天内，累计涨跌幅分别为 4%, 4.9%和 8.8%。

---

Open or Close?

在示例中我们使用的是收盘价。正确的做法一般是传递开盘价给 prices 表格，alphalens 会保证对 T 日的因子，使用 T+1 的价格作为入场价格，T+N+1 的价格作为退出价格。如果 N 为 1，则 T 期因子的一日回报为 $$ Ret=\frac{P_{t2}}{P_{t1}}-1 $$ 此外，一般不得让 T 期的价格参与 T 期的因子计算，这样会带来未来数据。正确理解这些细节，是实施好量化交易的关键。

接下来的分析，我们可以直接使用 create_full_tear_sheet 方法，来生成一个完整而全面的报告。不过，出于讲解的方便，我们将把 create_full_tear_sheet 方法拆开，一步步地分析它的实现。

回报分析

我们首先最关心的，可能是因子回报。回报分析尽管没那么可靠，但它既感性，又性感，毕竟，比起波动率、IC 这些客观但毫无感情而言的统计学概念而言，我们都更喜欢钱！

from alphalens.performance import mean_return_by_quantile

mean_return_by_q_daily, std_err = mean_return_by_quantile(
    factor_data, by_date=True)

mean_return_by_q_daily.head()

我们得到的结果如下：

---

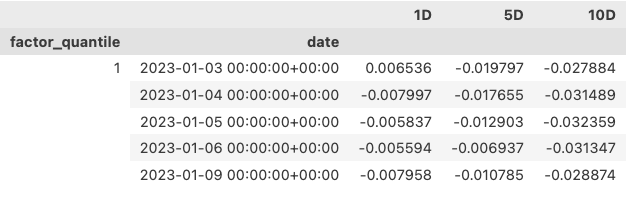
结果只显示了第 1 组的前几期数据。这个数据过于详尽，作为概览，我们更希望给出它的摘要信息。这可以通过设置 by_date = False 来实现：

这样我们得到的因子分层第一组，它的日回报是0.063%。如果按250天来计算年复利的话，我们会得到年化17.05%的回报，就凭这一个因子，你已经秒了98%以上的公墓（此处无错别字）基金经理了！

---

Info

如果你要复现此处结果的话，请注意分层方法选 quantiles = 10，而不是bins=10

与之配对的绘图函数是 plot_quantile_returns_bar:

import seaborn as sns
from alphalens.plotting import plot_quantile_returns_bar

plot_quantile_returns_bar(mean_return_by_q_daily)
sns.despine()

这里我们使用了seaborn的despine函数来去掉上方和右边的spine线。

从图来看，这个因子不错。它表现出较好的单调性，也就是随着分组号增加，因子表现在变差。注意，我们的因子是换手率因子，在分层中，组号低的，正好就是低换手率! 如果因子能表现出较好的单调性，我们不仅可以靠做多获得收益，还可以通过做空来使收益倍增！

---

不过，单凭一个日均收益来判断因子不太可靠，我们还得看看回报的统计学特征，看看这些收益，是否是由少数几笔意外收入贡献的。这时候我们就需要violin图：

from alphalens.plotting import plot_quantile_returns_violin

plot_quantile_returns_violin(mean_return_by_q_daily)
sns.despine()

Note

此时要注意， 在生成mean_return_by_q_daily时，by_date参数必须为True。否则，我们得到的是一些标量，是不具有统计学特征的。

我们得到的图如下：

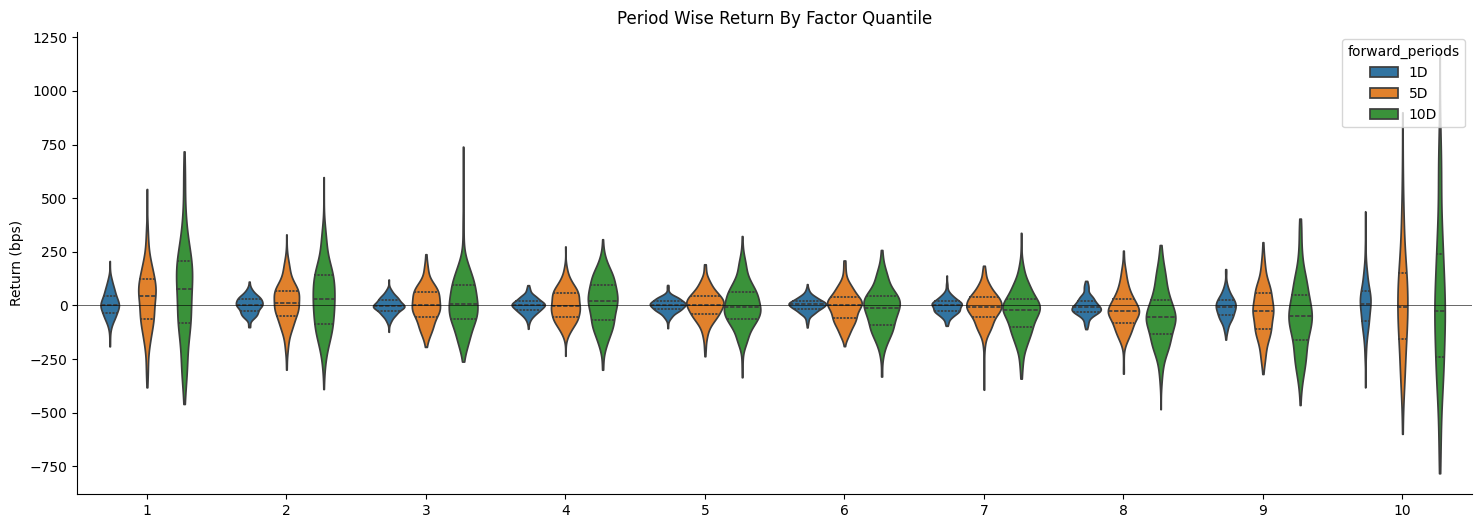
我们来分析第1组的数据。可以看出（当然图有点小，你可能啥也看不出来，自己拿数据试吧！），至少比较接近正态分布，没有很长的尖峰，这说明正的收益并不是少数几笔带来的。反观第3组的10日收益，它出现了很长的尖峰，这说明可能出现了离群值。

---

我们还可以查看最大的一组因子与最小的一组因子之间的利差。

from alphalens.performance import compute_mean_returns_spread
from alphalens.plotting import plot_mean_quantile_returns_spread_time_series

qrs, ses = compute_mean_returns_spread(mean_return_by_q_daily,upper_quant=1, lower_quant=9,std_err=std_err)

plot_mean_quantile_returns_spread_time_series(qrs, ses)

最终我们得到了下图（这里只取了1天）：

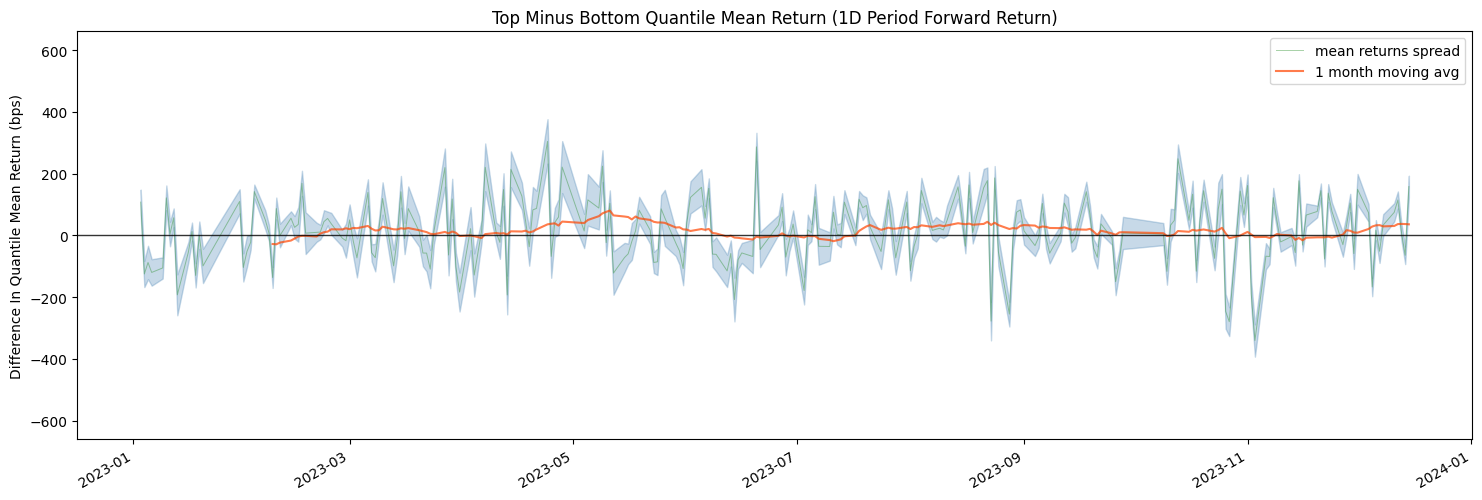
红色的线是月线。我们可以看到，多数时间，它比较明显地、稳定地居于零轴之上，这说明，基于低换手率的多空策略，能取得较好的收益。

重要提示

在计算多空利差时，compute_mean_returns_spread函数需要我们指定upper_quant和lower_quant。在这里，upper_quant是第一组，而lower_quant从前面的分析来看是第9组，而不是第10组。

最后，我们以累积回报率分析作为本篇笔记的结束。这可能也是初学者最喜欢的曲线：

---

from alphalens.plotting import plot_cumulative_returns_by_quantile

mean_return_by_q_daily, std_err = mean_return_by_quantile(
    factor_data, by_date=True)

plot_cumulative_returns_by_quantile(mean_return_by_q_daily, period='1D')

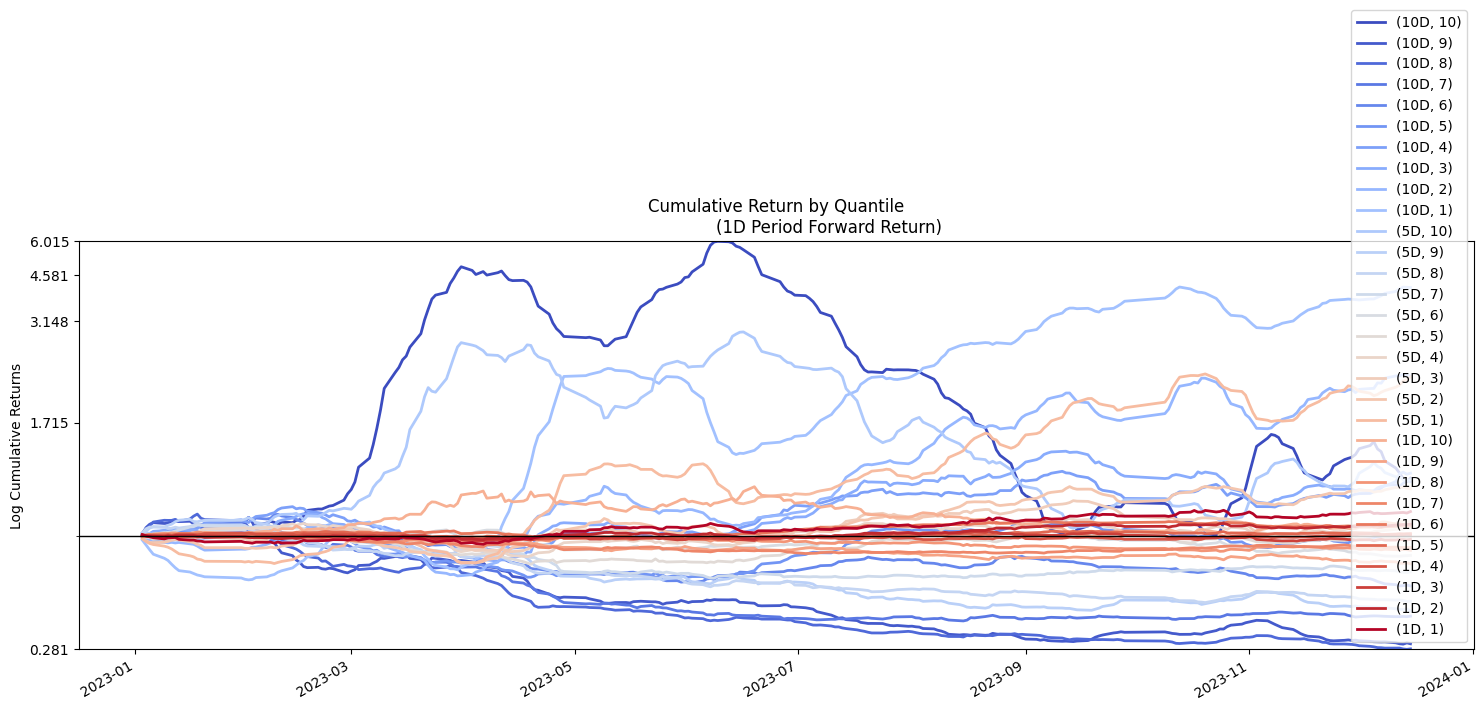
我认为这里alphalens出现了一个错误。我们要求它只绘制以1天为单位的各分层的累积回报，但它却附赠了5天和10天的轨迹，但这增加了读图的难度，因此我们并不领情。

从累积回报图来看，如果我们能把该因子与一些正确的择时因子组合在一起，就能获得巨大的收益。即便如此，在1日累积回报中，最好的（也就是分组为1）数据表明，仍然能实现一个正收益。

刚刚我们展示的是分层因子回报。Alphalens还提供了因子作为整体的回报计算和绘图。在我们这个例子中，这样做并没有意义，因为是低换手率产生价值，而不是_~换手率~产生价值。