因子分析（3）- 都是坑！这么简单的Alpha计算，竟然错了？！

我们继续 Alphalens 因子分析报告的解读。在过去的两篇笔记中，我们都提到，运用 Alphalens 进行因子分析步骤很简单，但是如果不了解它背后的机制与逻辑，很容易得到似是而非的结论。

Alphalens 提供了alpha和beta分析。方法是factor_alpha_beta：

from alphalens.performance import factor_alpha_beta

alpha, beta = factor_alpha_beta(factor_data)

我们将得到以下输出：

---

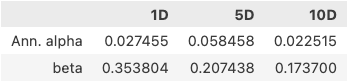
看上去很完美。

这个结果表明，该因子的年化alpha是2.7%，风险暴露为35%，一定程度上受到市场影响。我们按照 Alphalens 的要求，通过 get_clean_factor_and_forward_returns 方法获得了 factor_data, 然后用它来计算 alpha 和 beta。过程简单明了，似乎不可能出任何错误。

但实际上，如此得到的 alpha 和 beta，在我们这个示例中并没有任何意义。

Warning

在做量化研究时，我们需要对得到的任何数值都进行仔细的研究，不能轻信任何一个结果，因为有结果和结果正确完全是两回事。

在Alphalens中，alpha和beta是通过因子组合收益对市场组合收益的最小二乘回归（OLS）来求得的。

Info

Alphalens在这里借用了statsmodels中的OLS方法。

其中，市场组合的收益是对各标的收益的简单平均。假设我们的组合共有4个标的，某一日它们各自的收益分别为: 0.01189, 0.01102, -0.01241和-0.01898，则当日市场组合的收益为

\[ (0.01189 + 0.01102 -0.01241 -0.01898)/4= -0.00212 \]

---

而因子组合收益的计算，涉及到因子权重的分配问题。因子分配权重\(W\)一旦确定，则则因子组合的收益就可由下列公式求出：

\[ r_p = \sum{r_i * W_i} \]

关键在于权重\(W\)的计算。

Alphalens是这样计算的：它将factor_data按天进行分组，然后对将每个asset的因子除以因该组因子之和，这样得到的结果，其和为1。此外，它还提供一个参数，以进行零均值中心化，即将因子值减去中位数，再除以该组因子之和，这样得到的因子权重之和将为零。

假若我们有以下factor_data(左图)，如果我们对上述factor_data，用Alphalens的方法求各因子的权重，我们将得到右图：

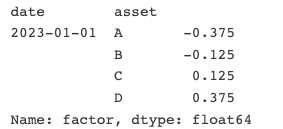
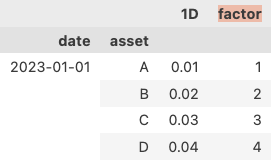
这里有两个问题：

1. 缺省地，Alphalens计算出的因子权重和为零，这适用于可以同时做多做空的市场。如果因为种种原因，你只能选择单边做多的话，那么我们调用factor_alpha_beta时，就必须将demeaned参数传值为False，以改变factor weights的计算。

---

1. 如果factor是换手率，则按照Alphalens分配的权重，该因子组合的收益率（假设demeaned = False）是这样计算得来的：给换手率最大的，分配最多的做多权重，给换手率最小的，分配最小的权重，而整个权重和为0。这样刚好和低换手率因子的作用相反！

所以，我们在构造因子时，需要考虑将factor进行转换，使之与因子收益率呈正相关关系。

现在看起来，这个结论似乎是那么显然易见，但是，alphalens并没有文档提示这一点，而且，我们在前面的其它分析中，由于使用了分层法，其分析结果并不受影响，所以这个问题，也就一直没有暴露。

现在，我们改造一下factor，重新运行：

from alphalens.utils import get_clean_factor_and_forward_returns

factor_data = get_clean_factor_and_forward_returns(factor, prices, bins=None, quantiles=10)

# 我们将换手率因子取倒数，从而使得因子逆序
factor_data.factor = 1 / factor_data.factor
factor_alpha_beta(factor_data,demeaned=False)

这一次，我们得到的年化alpha是4.48%。市场暴露风险为80%，这也与我们在累积收益图中看到的相一致。

现在，我们再做一次 mean_return_by_quantile 分析，看看有什么不同：

---

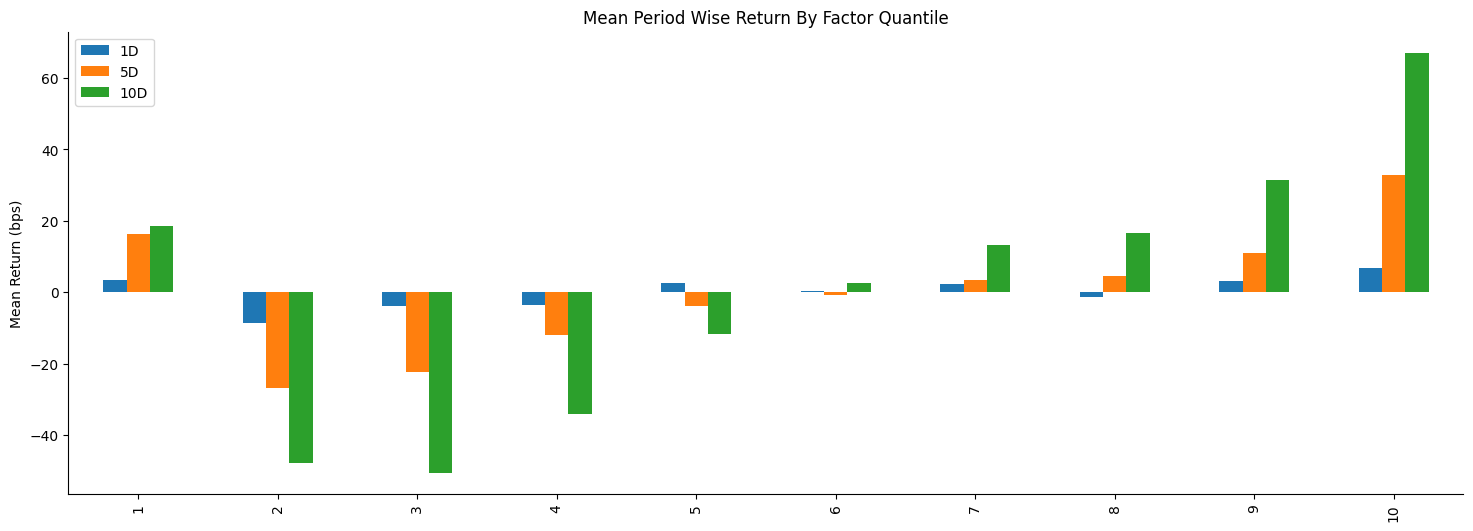
这个结果在视觉上，是昨天笔记中对应结果的水平翻转。这一次，表现最好的是第10组因子，最差的是第二组因子。除此之外，并没有其它的不同。

Tip

1. 默认地， alphalens计算收益是，会构建多空组合，即做多组号最大的分层，做空组号最小的分层。
2. 尽管文档没有要求，但经过代码分析，alphalens实际上要求因子值与收益呈正相关关系。
3. 如果因子值与收益刚好呈负相关关系，我们可以通过求倒数的方法，将因子值重新逆序。
4. 如果因子值与收益之间没有单调递增（递减）的关系 ，则因子检验失败，但需要我们自己去分析得出这个结论。
5. alphalens中，计算因子的alpha和beta是通过因子组合收益对市场组合的收益做OLS线性回归得到的。