Alphalens因子分析(4) - Information Coefficient方法

在前面的笔记中，无论是回报分析，还是因子Alpha，它们都受到交易成本的影响。信息分析 (Information Analysis)则是一种不受这种影响的评估方法，主要研究方法就是信息系数(Information Coefficient)。

---

信息系数的范围为-1到1，绝对值越大，表明因子与收益之间的相关性越强；绝对值越小，表明因子对收益的贡献越小；因此，0表示因子对收益完全不产生贡献，1表示完美的线性关系（预测能力好），-1则表示因子与收益完全负相关，这也是预测能力强的一种表现。

我们通过factor_information_coefficient方法来求因子的IC：

from alphalens.performance import factor_information_coefficient
ic = factor_information_coefficient(factor_data)

ic.head()

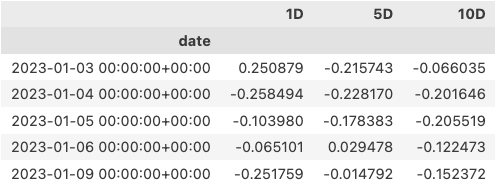
当然研究时间序列的最好方式还是可视化：

---

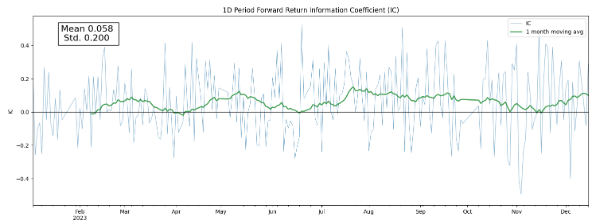
从这个图上我们能看出来什么？IC的均值似乎很接近于零。按照IC的定义，这是不是说明，低换手率因子与预测涨跌几乎没有关联，因而不值得我们考虑这个因子？

在下结论之前，我们先看看我们得到的IC的分布信息究竟如何：

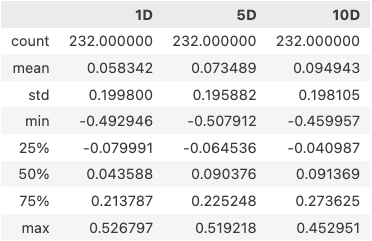
它的均值只有0.058，最大值也只有0.52。距离理想值1确实有点大。不过，是否这真的意味着换手率因子不行呢？

我们先来看看聚宽因子库中，最好的因子IC均值是多少。

聚宽是一家百亿私募，他们也提供了类似quantpian一样的众包平台。在它的网站上有一个栏目叫因子看板，我们把他所有的因子都列出来，按IC均值降序排列：

---

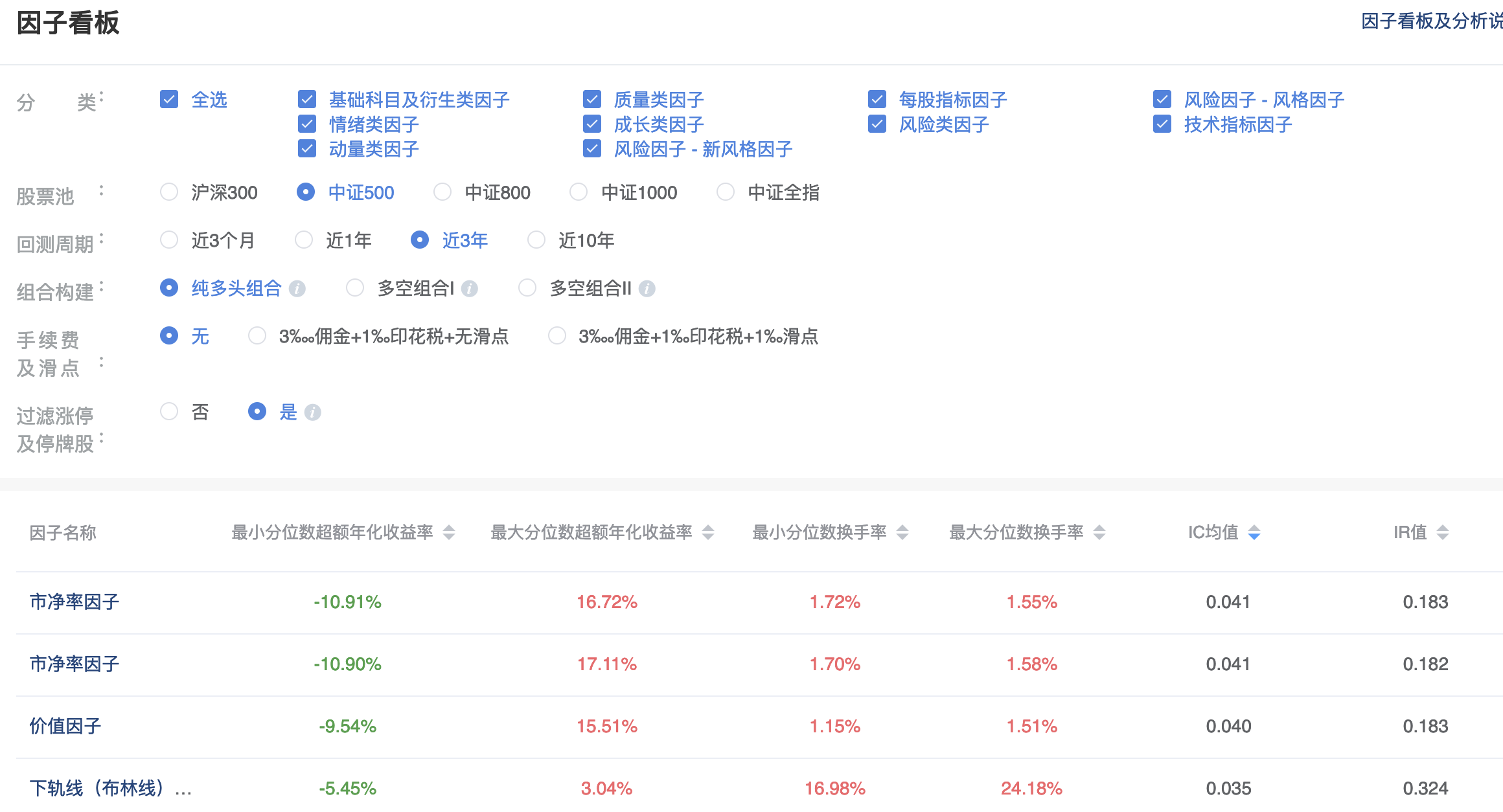
聚宽的三年期因子中，IC均值最大的是0.041，因此，我们这个因子的预测能力，已经超出了聚宽因子库中的所有因子。

实际上，聚宽因子库也很认可换手率因子，收纳了多个换手率相关因子，比如有年度平均月换手、5日平均、20日平均、60日平均和240日平均换手等。

其中年度平均月换手率因子的IC是-0.035，年化是13.39%。不过，这些因子并不是开源的，它们是如何实现的，就不得而知了，我们只能从名字上猜测，它们利用了换手率数据。

出于好奇，我们也把这个问题抛给了GPT4。提问中，我们先确定了GPT的版本是GPT4，并且它的资料库更新到了2023年4月：

---

GPT4的回答是，IC均值在0.05以上，就表明因子的预测能力很强了。理论中的最佳值是1，因子预测中的最佳预期是0.05。理想很丰满，现实很骨感。

当我们使用随机变量的均值时，我们常常会担心这个均值是否受到了少数极值的影响。我们可以通过标准差来度量，不过最直观的方式是通过直方图，或者QQ图进行分析：

---

from alphalens.plotting import plot_ic_hist

plot_ic_hist(ic)

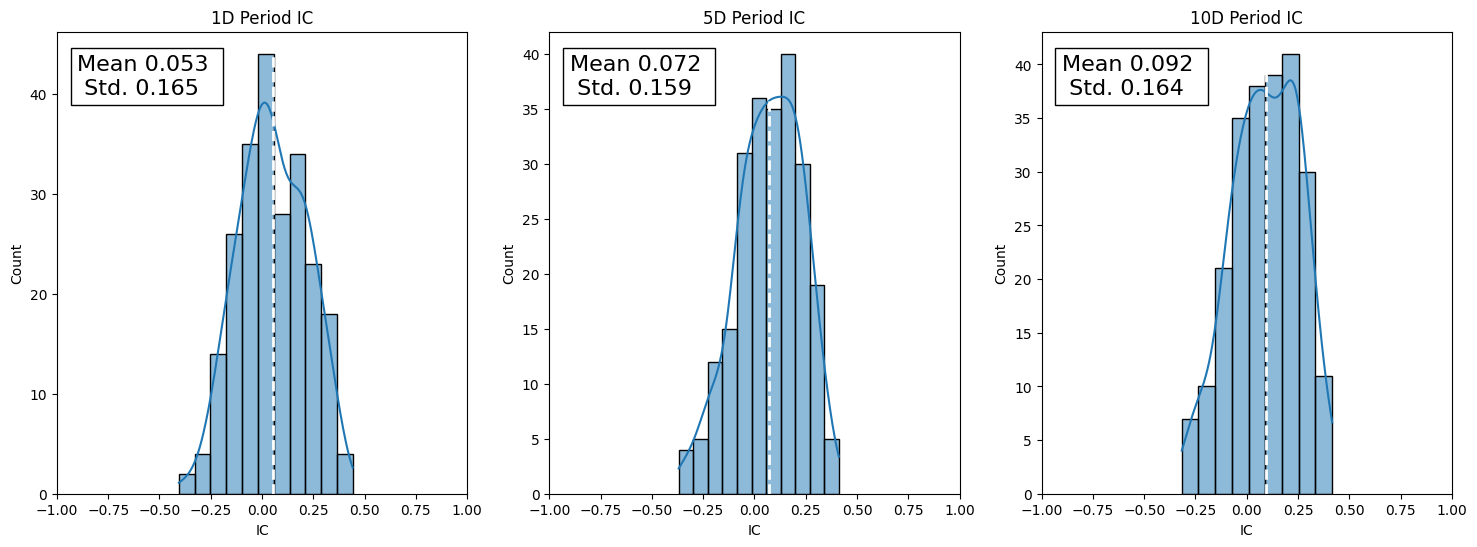
看直方图关键是要看多数时间IC的表现如何，何处IC值很可能下降，以及是否存在肥尾。我们仍然要非常有经验，才能看出来IC的分布好坏。如果借助QQ图，观察要容易很多：

from alphalens.plotting import plot_ic_qq

plot_ic_qq(ic)

---

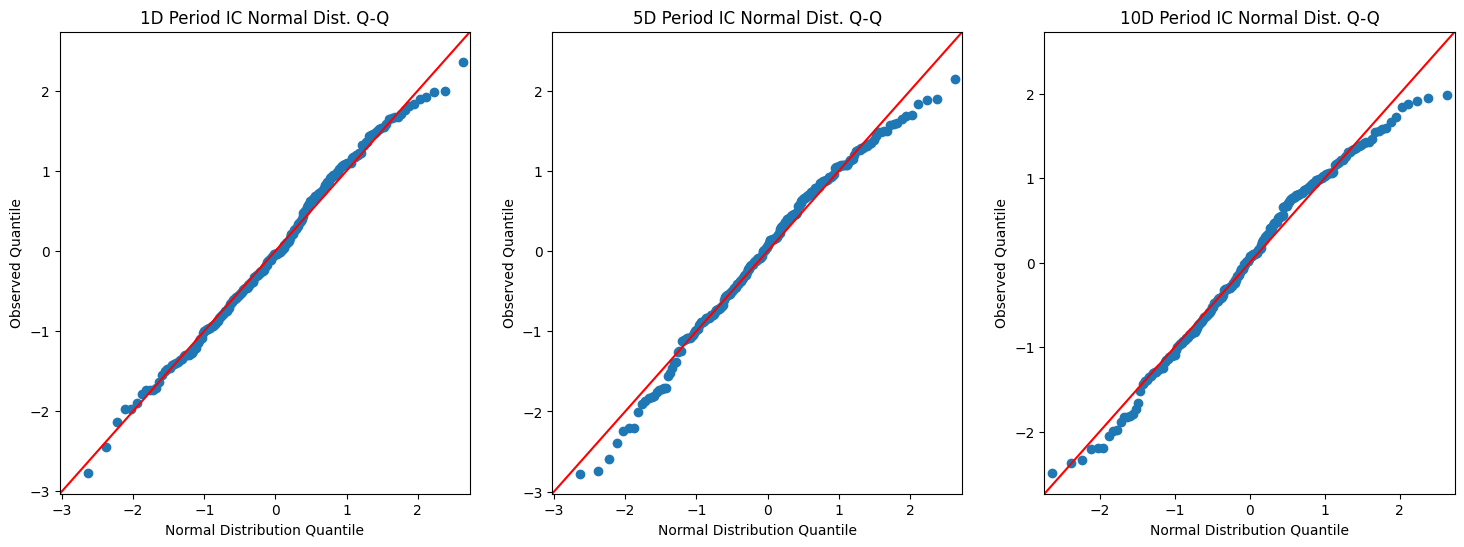
QQ图能显示IC值分布与正态分布之间形状的差异。特别是对了解分布中最极端的数值是如何影响预测能力的特别有帮助。

从QQ图可以看出，1日换手率因子的表现相当好。多数点落在对角线上。

最后，作为一个快捷方式，Alphalens允许我们调用create_information_tear_sheet来一次性获取所有的信息分析数据：

from alphalens.tears import create_information_tear_sheet

create_information_tear_sheet(factor_data)

这将把今天笔记中出现的所有图，以集中显示的方式绘制一次。

这里要传入的factor_data，是一切的起点。我们在第一篇笔记中对它作过介绍，它是通过utils包中的get_clean_factor_and_forward_returns来获得的。

Tip

1. IC分析显示因子与收益的相关性，去除了交易成本影响
2. IC均值的绝对值在0.02~0.05，就表明因子有一定预测能力。
3. IC均值的绝对在0.05以上时，就表明因子有较强的预测能力。
4. 1日低换手率因子的IC值在0.05以上。