提速100倍！QMT复权因子高效算法

QMT的XtQuant库提供了量化研究所需要的数据。它在一些API设计上面向底层多一些，应用层在使用时，还往往需要进行一些包装，比如复权就是如此。

这篇文章介绍了将XtQuant的除权信息转换成常常的复权因子的高性能算法。与官方示例相比，速度快了100多倍。

Info

通过XtQuant的API get_market_data_ex，我们可以直接获得经过前后复权处理的行情数据。但是，如果你希望自己使用更高效的方式来存储行情数据的话，就需要存储未复权的原始价格数据和复权因子，在需要使用前后复权价格时，根据选择的时间区间，临时计算复权价格。这就需要也存储复权因子。

XtQuant没有提供复权因子，相反，它通过 get_divid_factors 方法提供了更详尽的分红、送股、配股信息。数据如下所示：

date	interest	stockBonus	dr
20121019	0.100	0.0	1.007457
20130620	0.170	0.6	1.614093
20230614	0.285	0.0	1.025261

提供的信息非常全，但要利用这些数据来进行价格复权，会比较烦琐。在量化中，多数场合我们可以仅使用复权因子（factor-ratio）来计算前后复权价格。这就需要将上述信息转化为复权因子。

XtQuant的示例中，已经提供了一个由上述信息，计算复权因子的示例。由于它是示例性质的，所以在代码逻辑上需要做到简单易懂，因此它在计算中，使用了循环，而不是向量化的运算方法。

这是官方给出的示例代码:

def gen_divid_ratio(bars, divid_datas):
    drl = []
    dr = 1.0
    qi = 0
    qdl = len(bars)
    di = 0
    ddl = len(divid_datas)
    while qi < qdl and di < ddl:
        qd = bars.iloc[qi]
        dd = divid_datas.iloc[di]
        if qd.name >= dd.name:
            dr *= dd['dr']
            di += 1
        if qd.name <= dd.name:
            drl.append(dr)
            qi += 1
    while qi < qdl:
        drl.append(dr)
        qi += 1
    return pd.DataFrame(drl, index = bars.index, 
                        columns = bars.columns)

# 获取除权信息
dd = xtdata.get_divid_factors(s, start_time="20050104")

# 获取未复权行情
bars = xtdata.get_market_data(field_list, ["000001.SZ"], 
                                '1d', 
                                dividend_type = 'none', 
                                start_time='20050104', 
                                end_time='20240308')
%timeit gen_divid_ratio(bars["close"].T， dd)

这段代码计算了000001.SZ从2005年1月4日以来的复权因子。如果当天没有发生除权，则当天因子从1开始，后面每发生一次除权除息，因子就在前一天的基础上增加dr倍。因此，这样算出来的复权因子，一般情况下是一个以1开始的递增序列。

在notebook中运行时，上述代码的执行时间是407ms±14ms。

下面，我们就介绍如何将其向量化，将速度提升100倍。

def get_factor_ratio(symbol: str, start: datetime.date, end: datetime.date)->pd.Series:
    """获取`symbol`在`start`到`end`期间的复权因子

    复权因子以EPOCH日为1，依次向后增加。返回值取整个复权因子区间
    中[start, end]这一段。

    Args:
        symbol: 个股代码，以.SZ/.SH等结尾
        start: 起始日期，不得早于EPOCH
        end: 结束日期，不得晚于当前时间

    Returns:
        以日期为index的Series
    """
    if start < tf.int2date(EPOCH):
        raise ValueError(f"start date should not be earlier than {EPOCH}: {start}")

    start_ = tf.date2int(start)
    end_ = tf.date2int(end)
    df = xt.get_divid_factors(symbol, EPOCH)

    df.index = df.index.astype(int)
    frames = pd.DataFrame([], index=tf.day_frames)
    factor = pd.concat([frames, df["dr"]], axis=1)
    factor.sort_index(inplace=True)
    factor.fillna(1, inplace=True)

    query = f'index >= {start_} and index <= {end_}'
    return factor.cumprod().query(query)["dr"]

我们设置的EPOCH时间是2005年1月4日。这一年是全流通股改启动之年。以此为界，上市公司在治理结构上发生了较大变化，因此，进行量化回测，似乎一般也没必要使用在此之前的数据。

Info

罗马不是一天建成的。股改也是这样。在此后相当长一段时间内，你还能看到一些股票的名字以S开头，意味着该股还未完成股权分置改革。不过，尽管如此，我们也只能以大多数为主。很多人以为量化是一个纯算法的活儿。但是，了解脏数据、处理脏数据，对收益的影响并不比算法少。

这段代码的核心逻辑是，dd['dr']是一个带时间戳的稀疏数据。我们首先要把它展开成：

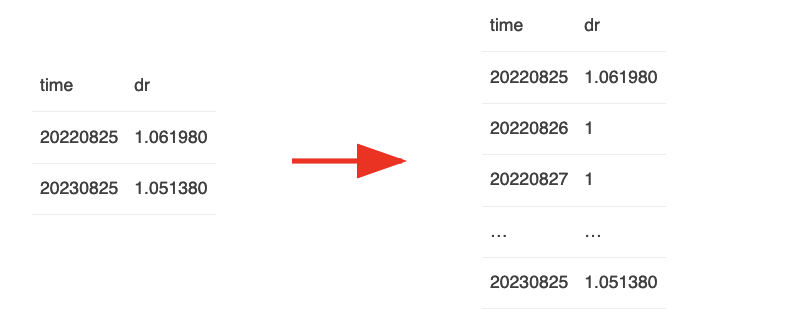
在此基础上，通过一个cumprod运算，我们就可以求出符合要求的factor ratio。

第一步的运算实际上是一个join运算。我们使用一个在交易日上连续的空的dataframe与上述dd['dr']进行join，其结果就是，如果记录在dd['dr']中存在，就使用dd['dr']中的数值，如果不存在，就使用空值。

然后我们使用pandas.fillna来将所有的空值替换为1.最后，由于我们只需要在[start,end]期间的因子值，所以通过datataframe.query来进行过滤。

上述代码将得到与官方示例一致的结果，但执行时间仅3.96ms±251，比使用循环的版本快了100倍还多。

本方法是作为zillionare接入XtQuant数据的方案的一部分开发的。在这个方案中，我们将采用clickhouse来存放行情数据，以获得更好的回测性能。因此，我们还必须考虑到每种数据如何进行持续更新。这个更新的大致思路是，我们把上述计算中得到的factor ratio存入clickhouse中，在每日更新时，先取得所有股票的factor ratio的最后更新日期(T0)，以此日期为下界，调用xtdata.get_divid_factors来下载最新的除权信息，通过同样的方法求得T0日以来的因子，乘以T0日因子值，即可存入到clickhouse中。

Zillionare接入XtQuant的版本将是2.1，预计在6月发布。