跳转至

1赔10！中证1000应该这样抄底

3月28日那篇文章分析了前一日的下跌为什么是可能预见的。这一篇文章，我将用坚实的统计数据，说明这一天为什么应该抄底，预期的损益比又是多少。

抄底不是贪婪。抄底是拿先手，以降低风险。在至暗时刻，请铭记，没有最终的成功，也没有致命的失败，最可贵的是继续前进的勇气！

赔率与收益期望计算

3月27日，沪指下跌1.26%，中证1000下跌3.33%，亏钱效应明显。在第14课中，讨论过这样一个问题，沪指下跌4%时，此时抄底成功的概率有多高？我们借这个问题，讨论了PDF/CDF的概念，并且给出了通过statsmodels中的ECDF、numpy/scipy中的相关方法求解的思路。

但在现实中，可能更有实际意义的问题是当A股连续下跌到x%时，此时抄底，预期盈亏比，也就是所谓的赔率会有多大？。刚好，在今年的3月27日，我们就遇到了中证1000收盘时，连续下跌达6.943%的情况，随后连续反弹，上涨达5.5%，收益相当可观。

要解决这个问题所需要的知识，我们在前面的课程中已经做好了所有的知识铺垫。这里面最重要的方法，是在第9课介绍的find_runs。

它的作用是，将数组划分为若干个具有相同连续值的分组，返回这些分组的值、起点和长度。

有了这个方法，我们就可以根据每日收益率，找出每个连续下跌区间的端点，并计算该区间的pnl:

1
2
returns = bars.close.pct_change()
v, s, l = find_runs(returns <= 0)

returns数组是每日收益率。通过returns <= 0表达式，我们将获得一个二值数组，元素为True的部分，意味着当天没有上涨（下跌或者平盘）。

我们将得到如下结果：

结果将是一个三元组的数组，每一个元素由(v, s, l)组成，分别代表当前分组的值、起始位置和长度。

接下来，我们遍历这个数组，根据s和l找到区间的起始点和结束点，再用两个端点的收盘价就可以计算出区间的涨跌。下面的代码中，我们只计算了下跌区间：

1
2
3
4
5
6
7
8
close = bars.close
cum_neg_returns = []
for vi, si, li in zip(v, s, l):
    if vi and li > 1:
        cum_neg_returns.append((bars.frame[si-1], bars.frame[si + li - 1], close[si + li - 1]/close[si-1] - 1))

r = pd.DataFrame(cum_neg_returns, columns=["start", "end", "cnr"])
r

我们得到了116个结果：

50%

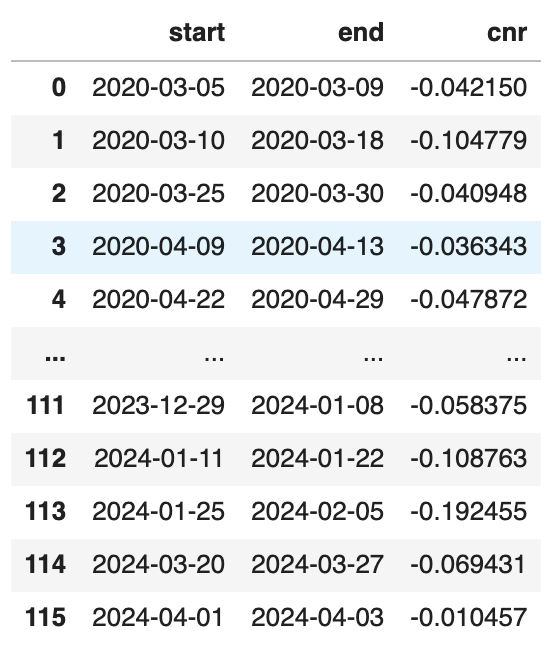
在3月27日收盘时，我们所处的位置对应上表中的第114行，也就是从3月20日起到27日，中证1000发生连续下跌，幅度为6.94%。

那么，继续下跌的概率是多少呢？它相当于(s < x).sum()/len(s)，我们换一个方法：

1
2
p_decline = r.cnr.le(-0.06943).mean()
p_decline

输出结果将是0.0862，也就是从过去4年的统计数据来看，连续下跌超（含）2天的共有116次。在这116次中，如果收盘跌幅达到6.943%，则继续下跌的概率为8.62%，也就是将有91.38%的概率反弹。

如果不反弹，我们就要蒙受抄底的损失。这个损失的期望是多少呢？我们统计一下，下跌6.94%后，继续下跌的情形是：

1
r[r.cnv < -0.0694]

50%

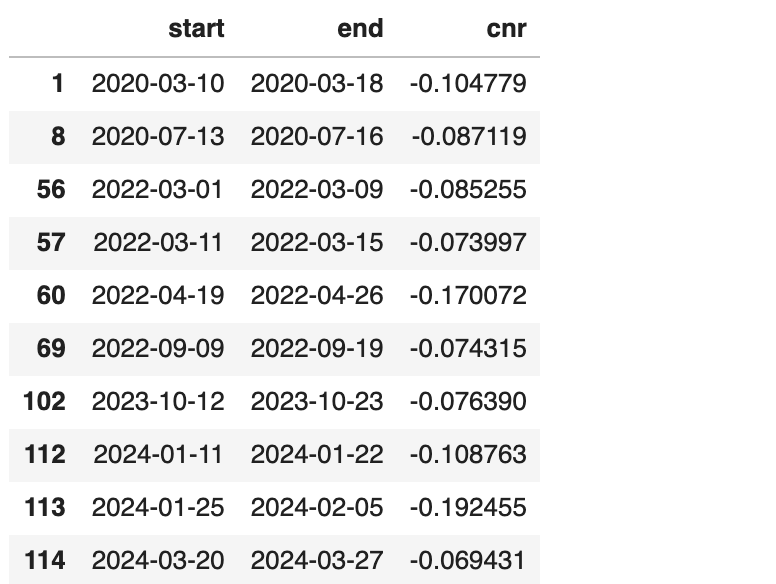
其预期是：

1
2
3
4
# 抄底失败的亏损预期

exp_lose = (r[r.cnr<-0.06943].mean() - (-0.0694))
exp_lose

抄底失败，也就是继续下跌的情形共有10次，平均损失是-10%左右，考虑到我们是在-6.94%时才抄的底，因此，我们将蒙受3.48%左右的损失。请记住，发生这种情况的概率只有8.62%。

如果反弹，我们将得到多少收益呢？这个计算略困难一点。在3月27日之后，反弹达到了5.5%。我们只有这样一个采样数据，但不能保证每次都会有这么大的反弹。

我们考虑一个保守一点的情况，即把下跌[-5%, -6.943%]间的所有反弹都当成下跌-6.943%以后的反弹。显然，在快速下跌中，下跌越多，反弹就越强，我们这样估算，肯定要比每次下跌-6.94%之后的反弹要低估了。不过，这样也使得我们的模型具有了额外的安全边际。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
# 抄底时间为bounced
bounced = [f.date() for f in (r[(r.cnr >= -0.0695) & (r.cnr<-0.05)]["end"])]

# 抄底收益为bounced之后，连接上涨的收益

cum_pos_returns = []
for vi, si, li in zip(v, s, l):
    end = tf.day_shift(bars.frame[si], -1)
    if end in bounced:
        cum_pos_returns.append((bars.frame[si-1], bars.frame[si + li - 1], close[si + li - 1]/close[si-1] - 1))

1
2
profit = pd.DataFrame(cum_pos_returns, columns=["start", "end", "profit"])
profit

上述代码先找出反弹的时间，然后遍历之前得到的三元组，如果起始点的前一天是某个连续下跌区间的结束日，我们就计算这一组的收益。最终我们得到的收益预期是：

1
2
3
4
# 抄底的收益期望是

exp_win = profit.profit.mean()
exp_win

这个预期是3.299%。看上去与抄底失败的预期损失差不多，但是，计算赔率时，我们要加上实现概率：

\[ exp\_win * 91.38\% / (exp\_lose * 8.62\%) = 10.03\% \]

最后，我们计算抄底的总体期望为:

\[ exp\_win * 91.38\% + exp\_lose * 8.62\% = 2.71\% \]

如果是DMA，加上4倍杠杆，一次获利将在10%以上。

风浪越大鱼越贵？

几年以前，我的合伙人推荐我看塔力布的《黑天鹅》一书。说实在的，这本书前1/4可以说是封神，但看到后面，感觉有点难以落到实处，无法应用。

图片来自电影《黑天鹅》官宣剧照

题外话： 我更喜欢看娜塔莉.波特曼主演的《黑天鹅》。

不过，我从来没有停止对《黑天鹅》事件的思考。我想，换一个角度，关注黑天鹅事件，但把黑天鹅看成是一种低概率事件来加以研究，也未尝不可。虽然脱了《黑天鹅》一书的窠臼，但好歹也有了一个切入点。

但是，可能有人要问，为什么要去接下跌的飞刀？平平稳稳赚钱不好吗？这是因为，在这个市场，本来就缺少平平稳稳赚钱的机会。

如果不在低位拿到先手，拿到便宜的筹码，就很容易被套在山腰甚至山顶。实际上，如果3月27日你没有入场，那么近期的行情是难以把握的。

抄底！基于坚实的统计概率，拿到先手，立于不败之地，才是在这个市场活下来的不二法门。

额外的惊喜

在我们的计算中，如果抄底失败，我们是按最大损失进行了计提。但实际上，在一轮快速下跌中，下跌越狠，反弹力度就越大，读者可以自行验证。

这里要讲的是，我们对抄底失败，是按平均3%计提的损失。但我们没有计算在被套3%之后，反弹的情况。我们以今年1月25到2月5日下跌最狠的那一轮为例，如果我们在下跌6.94%时就抄底，我们真的会损失3%吗？

读者可以自行验证。实际上，这一轮跌得快，反弹力度也大。如果我们在下跌达到6%以后抄底，大概会买在中证1000的4984点，然后会遭受约13%的下跌，但最终会连续反弹到4993点，最终收益0.18%。