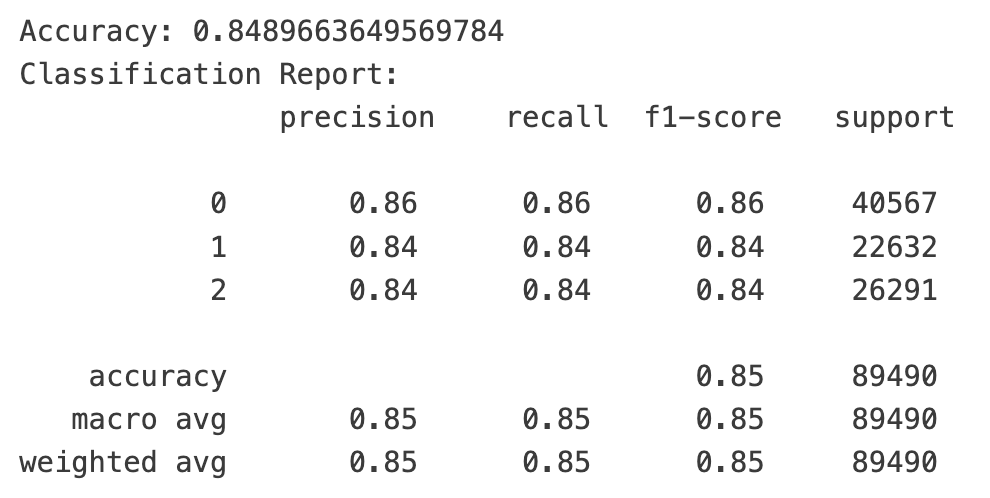
如果模型预测准确率超过85%，这台印钞机应该值多少马内？

在第13课中，拿决策树介绍了机器学习的原理之后，有的学员已经积极开始思考，之前学习了那么多因子，但都是单因子模型，可否使用决策树模型把这些因子整合到一个策略里呢？

在与学员交流之后，我已经把思路进行了分享。这也是我们第13课的习题，我把参考答案跟大家分享一下。

预告一下，我们训练出来的模型，在验证集和测试集上，三个类别的f1-score都取得到85%左右的惊人分数！

这个模型是如何构建的呢？

特征数据

首先是选定特征，我们选择了以下几个特征，都是我们在课程中介绍过、已经提供了源码的：

1. 一阶导因子。这个因子能反映个股一段时间内的趋势
2. 二阶导因子。这个因子能较好地预测短期趋势变盘。
3. RSI因子。经典技术因子，能在一定程度上预测顶底。
4. weekday因子。主要增加一个与上述量价信息完全无关的新的维度。

这些因子的实现如下：

def d2_factor(df, win: int = 2)->pd.Series:
    close = df.close/df.close[0]
    d1 = close.diff()
    d2 = d1.diff()
    factor = d2.rolling(win).mean()

    return factor

def rsi_factor(df, win: int = 6)->pd.Series:
    return ta.RSI(df.close, win)


def d1_factor(df, win: int = 20)->pd.Series:
    df["log"] = np.log(df.close)
    df["diff"] = df["log"].diff()
    return df["diff"].rolling(win).mean() * -1

def week_day(dt: pd.DatetimeIndex)->pd.Series:
    return dt.weekday

训练数据使用了2018年以来，到2023年底，共6年的数据，随机抽取2000支个股作为样本池。

start = datetime.date(2023, 1, 1)
end = datetime.date(2023, 12, 29)

np.random.seed(78)
barss = load_bars(start, end, 2000)

上述因子中，前三个因子都是时序因子。但我们挖掘这些因子时，都是通过alphalens进行挖掘的，alphalens通过分层对其进行了排序，所以，我们还要对上述因子按横截面进行排序，这样得到一些rank_*因子。这个方法相法于进行特征增广（Feature Augmentation）。

features = {
}

def rank_feature(feature):
    return feature.groupby(level=0).rank(pct=True)

for name, func in [("d2", d2_factor),
                   ("rsi", rsi_factor),
                   ("d1", d1_factor)]:
    feature = barss.groupby(level=1).apply(d2_factor).droplevel(0)
    features[name] = feature
    features[f"rank_{name}"] = rank_feature(feature)

# 计算rank
features = pd.DataFrame(features)
features['weekday'] = week_day(features.index.get_level_values(0))

for win in (1, 5, 10):
    features[f"ret_{win}"] = barss.groupby(level=1)["price"].pct_change(win)

features.dropna(how='any', inplace=True)
features.tail()

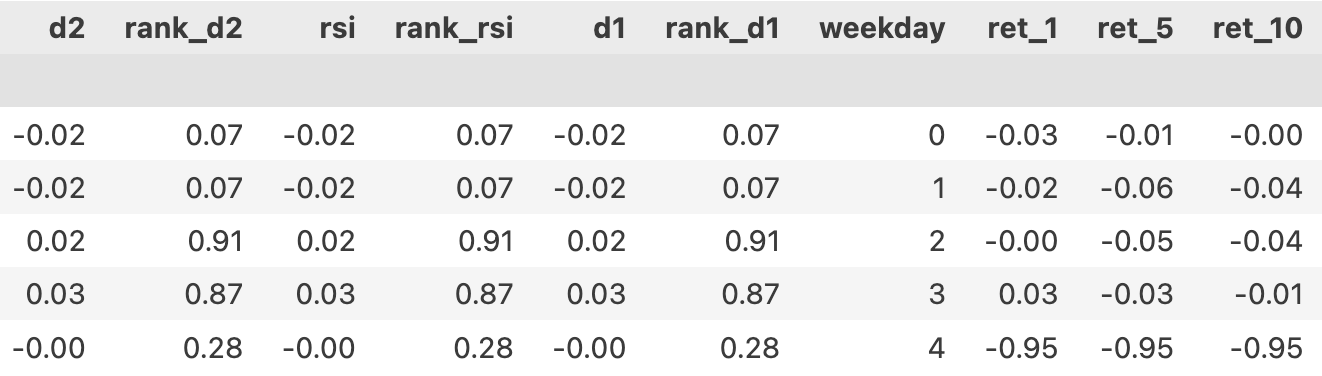
输出得到的是特征数据集。

其中的"ret_1", "ret_5", "ret_10"是每列对应的未来1，5和10日的收益率。这里延续了之前的做法，对每一个时间点T0，按T1开盘价买入，T2开盘价卖出的规则计算收益率。在训练模型时，一次只使用其中的一列。

回归还是分类？

现在，面临的选择是，如何将上述数据转化为可训练的数据。这里有三个问题：

1. 如何选择模型？即使我们确定要使用决策树，也还有一个问题，是要使用回归还是分类？
2. 如何划分训练集和测试集？这是所有问题中看起来最简单的一步。
3. 我们能把不同样本的数据同时作为训练的输入吗？这个问题看起来有点费思量。

从我们选定的特征来看，要让模型执行回归任务是有点太扯了，做分类更有道理，但也要进行一些转换。我们推荐的方案是使用分类模型，测试集划分先用sklearn自带的train_test_split来完成。

Tip

为什么说从选定的特征来看，不能让模型执行回归任务？把机器学习运用到量化交易，决不是照着模型的文档来套用这么简单，你必须深谙各个模型的原理，以及领域知识如何适配到模型。这些原理，在《因子分析与机器学习策略》中有讲解，老师还提供一对一辅导。

按分类模型进行训练之前，我们还要把ret_1转换成分类标签。转换方法如下：

from sklearn.model_selection import train_test_split

X = features.filter(regex='^(?!ret_).*$')
y = np.select((features["ret_1"] > 0.01, 
               features["ret_1"] < -0.01), 
              (1, 2), default=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

我们把涨幅大于1%的标注为类别『1』，跌幅大于1%的标为类别『2』，其余的打上标签『0』。标签0也可以认为是无法归类。

通过下面的代码进行训练：

from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, classification_report

# 初始化并训练模型
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)

# 预测并评估模型
y_pred = clf.predict(X_test)

print("Accuracy:", accuracy_score(y_test, y_pred))
print("Classification Report:\n", classification_report(y_test, y_pred))

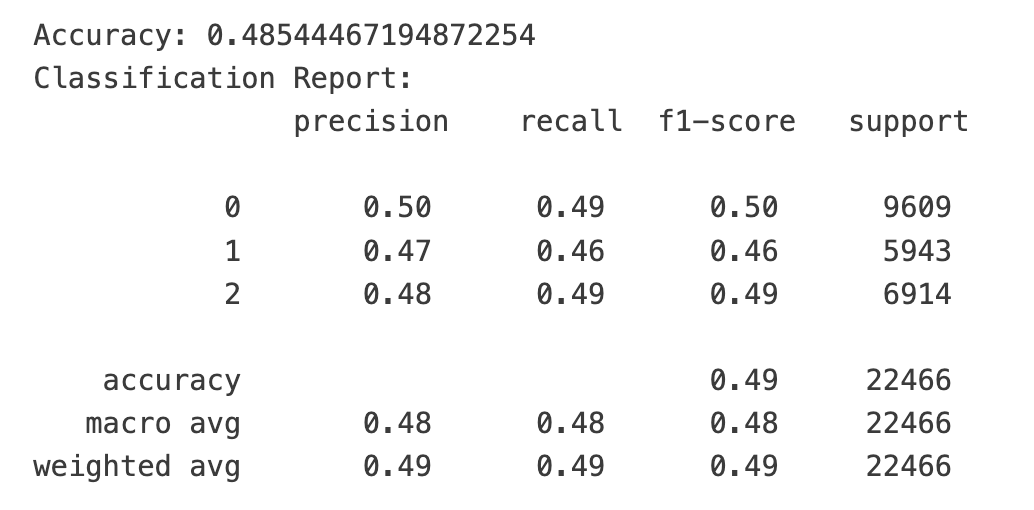
运行结果让人极度舒适。因为在一个三分类问题中，随机盲猜的准确率是33%，我们首次运行的结果就已经遥遥领先于随机盲猜了。

不过，三类目标的support数量并不均衡，这还是让我们有一点点担忧：目标0的分类一家独大，会不会导致准确率虚高？

再平衡！欠采样后，报告会不会很难看？

让我们先解决这个问题。我们可以采用一种名为欠采样(undersampling)的方法，分别抽取三类样本数中最小个数的样本数进行训练，这样一来，模型看到的训练数据就相对平衡了。

尽管undersampling实现起来很简单，不过，我们还有更简单的方法，就是使用imbalance库：

from imblearn.under_sampling import RandomUnderSampler

rus = RandomUnderSampler(random_state=42)
X_resampled, y_resampled = rus.fit_resample(X, y)

X_train_resampled, X_test_resampled, y_train_resampled, y_test_resampled = train_test_split(
    X_resampled, y_resampled, test_size=0.2, random_state=42
)

# 训练模型
clf_resampled = DecisionTreeClassifier(random_state=42)
clf_resampled.fit(X_train_resampled, y_train_resampled)

# 预测并评估模型
y_pred_resampled = clf_resampled.predict(X_test_resampled)

print("Resampled Accuracy:", accuracy_score(y_test_resampled, y_pred_resampled))
print("Resampled Classification Report:\n", classification_report(y_test_resampled, y_pred_resampled))

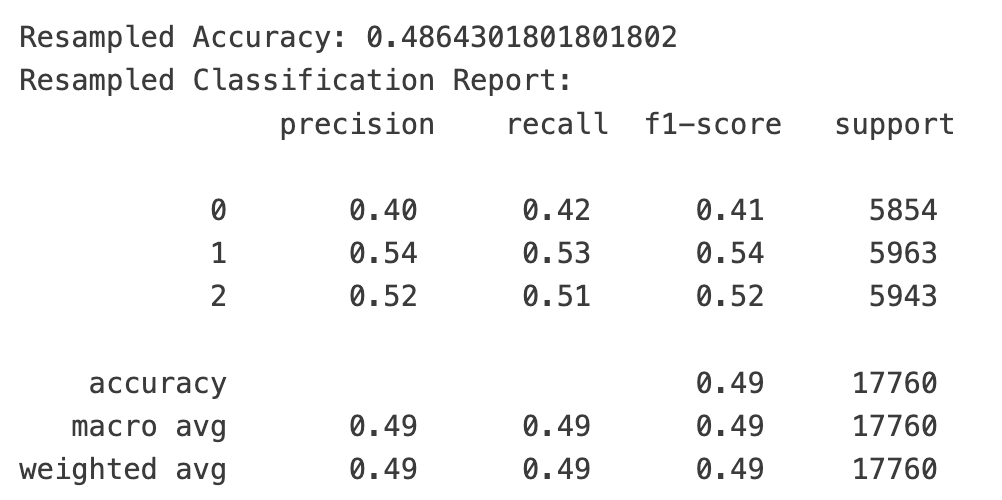
经过类别平衡后，准确率基本不变，但在我们关注的类别1和类别2上，它的准召率还分别提升了8%和3%。

Tip

imblearn还提供另一种平衡数据的方法，称为SMOTE（Synthetic Minority Over-sampling Technique），它通过复制或者合成少数类样本来平衡数据集。不过，合成数据这事儿，对金融数据来说，可能不太靠谱，我们宁可严格一点，使用欠采样。如果我们使用SMOTE方法进行过采样，训练后的模型在类别1和类别2上能达到60%和57%的f1-score。

为什么这么优秀？

我们刚刚得到的结果无疑是超出预期的优秀！

在欠采样平衡的版本中，如果模型预测次日买入会盈利，它的精确率是54%，也即在100次预测为盈利的情况下，有54次是正确的；而在余下的不正确的46次中，也只有18次是亏损，剩下的则是涨跌在1%以内的情况。

这个分析数据可以通过confusion matrix得到：

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
import matplotlib.pyplot as plt

cm = confusion_matrix(y_test_resampled, y_pred_resampled)

disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=clf_resampled.classes_)
disp.plot(cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.show()

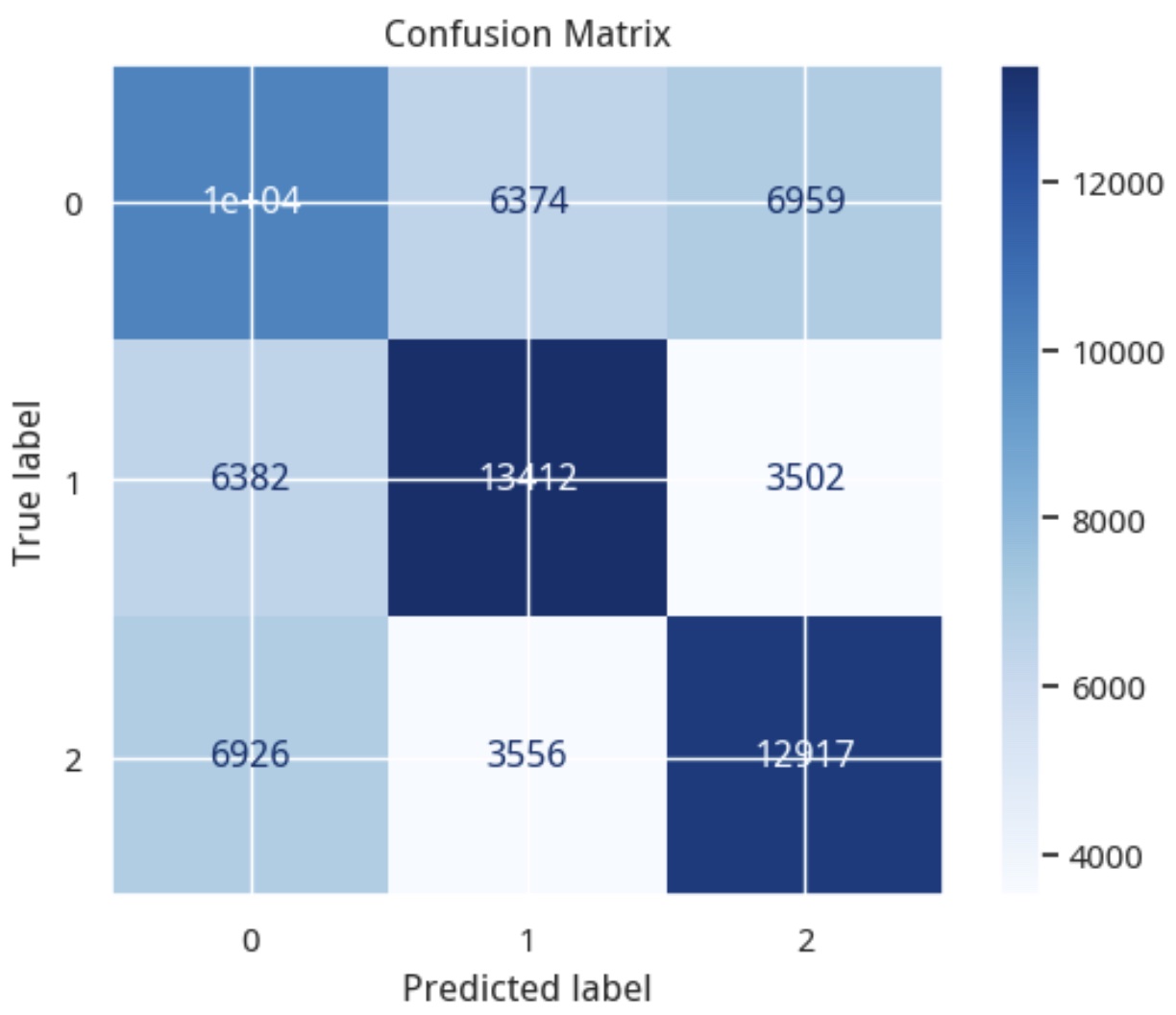
在上图中，预测分类为1的样本中，有15%（3556个）应该是下跌的样本，有27%（6374）个则是未知（或者平盘）的样本。

实际上，这是57：15的盈亏比例，或者说，已经达到了79%的精确率。这有多厉害呢？在索普的赌局中，他计算出赢的概率只要超过50%就会下注。因为只要胜得的天平偏向自己一点点，通过不断的累积中，高频交易最终会积累可观的利润！

这可能跟你在别处看到的模型很不一样。你可能从来没有想到过，机器学习模型在预测中竟然能如此有效。你可能开始寻找一些说辞，模型泛化肯定不好，这些数据只能代表过去等等。但其实这还只是前戏，高潮还在后面。

这个模型在构建过程中，固然还有一些可以探讨的地方，但它确实够好，原因是：

1. 我们提供了高质量的特征数据。我们没有盲目地追求特征数量。得益于我们在《因子分析与机器学习策略》课程前半部分的深入学习，我们很清楚，什么样的特征能够在一个模型中相融共洽，我们甚至能猜到每个特征在什么节点下产生什么样的贡献。
2. 我们知道特征能产生什么样的结果，于是使用了正确的任务模型（分类），并且使用了一定的构建技巧（gap）。

Tip

如果你想预测次日的价格呢?这不一定无法做到，在课程练习中，我们就给出过一个示例，在某种情况下能够预测价格可以达到的最高点。随着这些特征的增加，就会有更多的场景被覆盖。换句话说，要预测价格，你得提取跟预测价格相关的特征。

再思考：训练集与测试集的划分

将训练数据划分为训练集与测试集是机器学习中的一个非常基础的步骤。像很多其它教程一样，这里我们使用的是train_test_split函数。它简单好用，但并不适合量化交易。

它会随机抽取训练数据和测试数据，这样就撕裂开了数据之间的天然联系，甚至可能导致测试集数据早于训练集数据，从面可能产生未来数据的情况。

正确的做法是按时间顺序划分。在sklearn中还提供了名为TimeSeriesSplit的类，它能够为交叉验证提供正确训练、测试集划分。

你也可以使用我们之前介绍过的tsfresh库中的类似方法来完成这个任务。

不过，在这里，我们还用不上交叉验证，所以，我们手动将数据划分为训练集、验证集和测试集。

Tip

决策树并不支持增量学习。也就是说，你不能拿已经训练好的模型，在此基础上通过新的数据进行新的训练。在这种情况下，如果数据量不足，可能就不适合交叉验证。

from sklearn.tree import DecisionTreeClassifier

X = features.filter(regex='^(?!ret_).*$')
y = np.select((features["ret_1"] > 0.01, 
               features["ret_1"] < -0.01), 
              (1, 2), default=0)

n = len(X)
X_train = X_train[:int(n*0.7)]
y_train = y_train[:int(n*0.7)]

X_validation = X[int(n*0.7):int(n*0.9)]
y_validation = y[int(n*0.7):int(n*0.9)]

X_test = X[int(n*0.9):]
y_test = y[int(n*0.9):]


clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)

y_pred = clf.predict(X_validation)

from sklearn.metrics import accuracy_score, classification_report

print("Accuracy:", accuracy_score(y_validation, y_pred))
print("Classification Report:\n", classification_report(y_validation, y_pred))