hdbscan 聚类算法扫描配对交易 速度提升99倍
配对交易是一种交易策略,由摩根士丹利的量化分析师农齐奥.塔尔塔里亚在 20 世纪 80 年代首创。他现在是意大利雅典娜资产管理公司的创始人。该策略涉及监控两只历史上相关性较强的证券,并监控两者之间的价格差。一旦价格差超出一个阈值(比如 n 倍的标准差),价格回归就是大概率事件,于是交易者就做空价格高的一支,做多价格低的一支,从而获利。
 农齐奥.塔尔塔里亚
农齐奥.塔尔塔里亚
这种策略允许交易者在几乎任何市场条件下获利,因此一直是大型资产管理机构的主流策略。
例如,通用汽车和福特生产类似的产品(汽车),因此基于整体汽车市场,它们的股价走势相似。如果通用汽车的股价显著上涨而福特的股价保持不变,采用对冲交易策略的人就会卖出通用汽车的股票并买入福特的股票。假设股价会回到历史平衡点:如果通用汽车的股价下跌,投资者会获利;如果福特的股价上涨,投资者也会获利。

这个策略的正确性和有效性无可质疑,它几乎像数学定理一样完美。但是,如何才能找到这样的配对股资产呢?
显然,同行业的几家龙头公司,它们之间常常满足这样的关系。但是,正因为几乎所有人都知道其中存在着套利机会,市场的有效性就会在一定程度上对这种套利空间进行压缩。比如,如果你对过去几年的建设银行和工商银行执行配对交易策略的话,年化利润将不超过 1%。
而且,公司的业务形态总在发生变化,过去同质化竞争的企业,可能突然就因为收购、开拓新业务而不再是同一赛道的战友。老的赛道,也随时可能有新的掠食者加入进来。历史既在重复自己,也在开拓新的可能。
作为量化人,我们能够纯粹依赖数据分析,更加敏锐、快速找到这些新的机会吗?
答案是肯定的:我们可以仅凭资产的价格走势,通过协整检验,来发现可能的配对资产。
协整关系和平稳性
我们应该如何用数学的语言来描述像通用与福特之间的关系呢?这种关系在数学(更精确地说,在统计学上)上被称为协整关系。
要如何检验协整关系呢? Engle(恩格尔)和 Granger(格兰杰)在 1987 年提出了协整检验的两步法:先用 OLS 对两个变量 X 和 Y 进行回归,再用 ADF 检验 X 和 Y 是否平稳。他们俩人也因为在协整理论方面的开创性工作,获得了 2003 年的诺贝尔经济学奖。

这里又涉及到另一个概念,即平稳时间序列和平稳性检验。
平稳时间序列指随机变量的统计特性(如均值、方差、自协方差等)在时间上是不变的。比如,白噪声是平稳时间序列,它在均值和方差都是恒定的。下图显示了时间平稳序列(左上)和几种非时间平稳序列的对比:
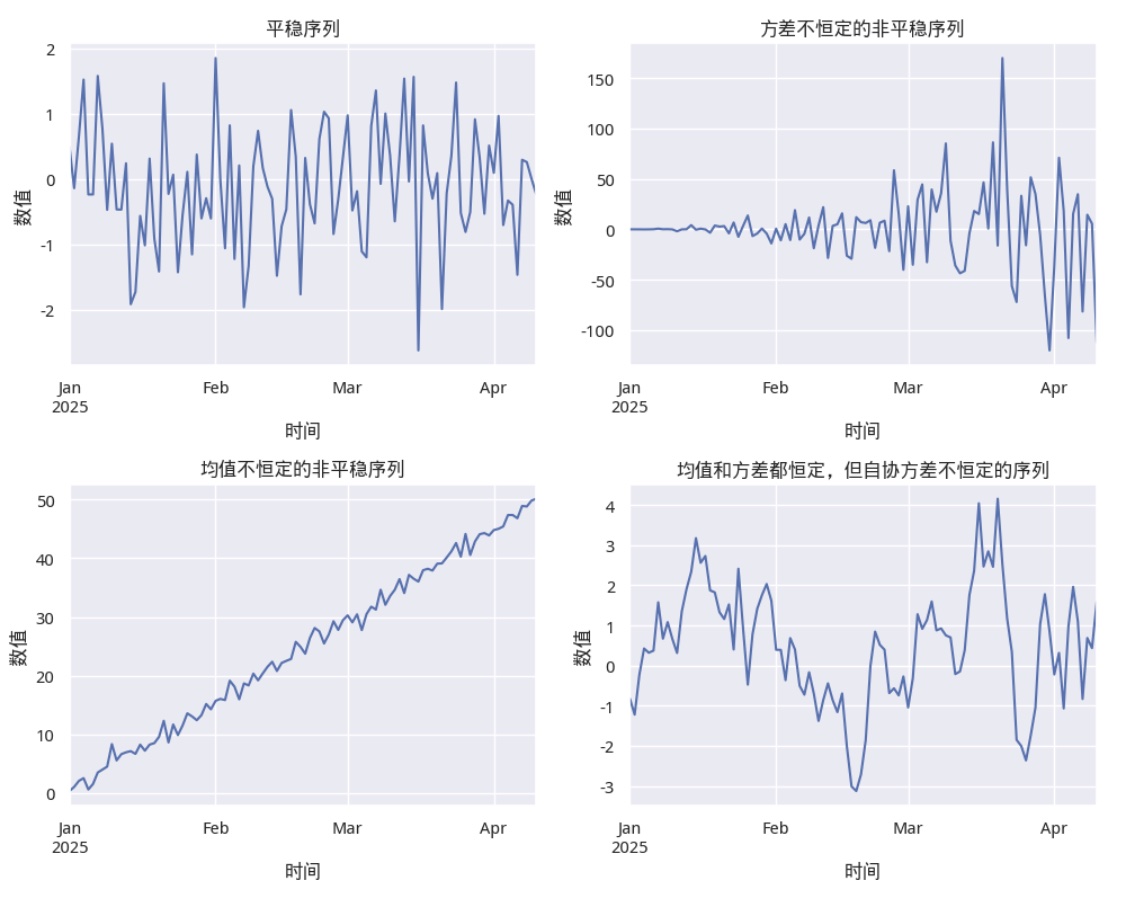
显然,对量化人来说,平稳时间序列有着非常有趣的特性:既然一个平稳时间序列的均值、方差恒定并且有自协相关特性,那么,一旦它偏离了均值,迟早都会回归到均值上,否则,它就不是平稳时间序列。
于是,基于一个假设条件(该时间序列过去和现在都是平稳时间序列,未来仍然也是),我们获得了难得的预言未来的能力!
检验一个时间序列是否平稳,一般使用 Dickey-Fuller 检验。

对量化人来说,资产价格序列和收益率是常见的两种时间序列。我们可以通过 Dickey-Fuller 检验来判断它们是否是平稳的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
start = datetime.date(2023, 1, 1)
end = datetime.date(2023, 12, 30)
barss = load_bars(start, end, ('000001.XSHE',))
close = barss.xs("000001.XSHE", level=1).close
returns = close.diff().dropna()
# 绘制平稳时间序列
plt.figure(figsize=(12, 6))
ax1 = plt.gca()
ax1.plot(close, label='Price')
ax1.grid(False)
ax2 = ax1.twinx()
ax2.plot(returns, label="Returns", color='orange')
ax2.grid(False)
lines, labels = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax1.legend(lines + lines2, labels + labels2, loc='best')
plt.show()
# 进行 ADF 检验
result1 = adfuller(close)
result2 = adfuller(returns)
df = pd.DataFrame({
"ADF Stat": (result1[0], result2[0]),
"P-Value": (result1[1], result2[1]),
"Critical Values 1%": (result1[4]["1%"], result2[4]["1%"]),
"Critical Values 5%": (result1[4]["5%"], result2[4]["5%"]),
"Critical Values 10%": (result1[4]["10%"], result2[4]["10%"]),
}, index=["close", "returns"])
df.T
|

这段代码显示结果如下:
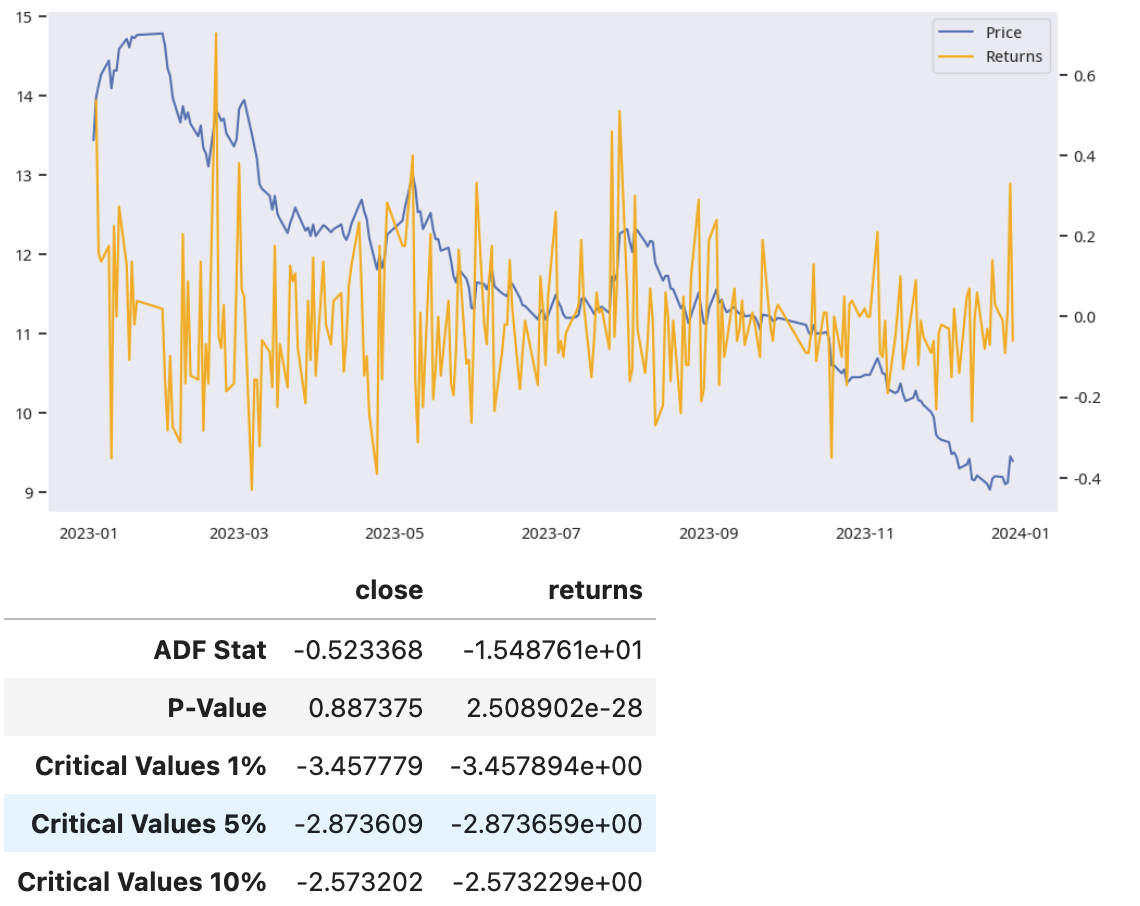
平稳性检验是协整检验的第二步。第一步则是对相关联的两个时间序列进行回归,构建残差序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
start = datetime.date(2021, 1, 1)
end = datetime.date(2023, 12, 30)
gsyh = "601398.XSHG"
jsyh = "601939.XSHG"
barss = load_bars(start, end, (gsyh, jsyh))
pair1 = barss.xs(gsyh, level=1).close
pair2 = barss.xs(jsyh, level=1).close
def hedge_ratio(price1: NDArray, price2: NDArray) -> float:
X = sm.add_constant(price1)
model = sm.OLS(price2, X).fit()
return model.params[1]
hr = hedge_ratio(pair1, pair2)
print(f"hedge_ratio 为:{hr:.2f}")
spreads = pair2 - pair1 * hr
result = adfuller(spreads)
if result[1] < 0.05:
print(f"p-value: {result[1]:.2f} < 0.05, 协整关系成立")
else:
print(f"p-value: {result[1]:.2f} > 0.05 协整关系不成立")
|
这段代码就完整地完成了一个协整检验。不仅如此,它还计算出了两个价格序列之间的对冲比(hedge ratio),正是通过 hedge ratio,我们才能构建出具有平稳性的价差序列。
不过,了解原理之后,一般情况下,我们并不会使用上面的方法来进行协整检验,因为 statsmodels 已经帮我们完成了所有这些工作:
| from statsmodels.tsa.stattools import coint
result = coint(pair1, pair2)
t, p_value, *_ = result
|
只要 p 值小于 0.05,我们就可以认为这两个时间序列是协整的。
性能问题
既然协整检验这么容易,那么,寻找配对交易的过程岂不是易如反掌?然而并不!
在一组资产池里,寻找协整对的计算量是一个组合数。如果资产池里有 100 支资产,计算量会是 4950 次。如果我们把资产池限定为国内资产,考虑到协整关系可能发生在 A 股、基金、期货和指数间,那么,资产总数在 1 万支左右,这样计算量就变成了接近 5000 万次。这个运算量实在是太大了。
在我们的课程环境里,运算 3 万次协整运算的时间约 20 分钟,也就是一次协整运算大约耗时 40 毫秒。所以,如果要完成近 5000 万次的协整检验,大概需要运行 24 天左右:来不及等你算完,长在你卫生间水管里的小虫子 -- 白斑蛾蚋已经走过了它的一生。

此时,聚类算法就可以发挥它的巨大威力了:如果我们能把这些资产分成若干簇,只在簇内进行协整检验,这样就可以大大减少协整检验的次数。
假设我们可以将样本聚类成\(K\)个簇,且每簇内样本数量分别为\(( N_1, N_2, \ldots, N_K )\), \(( \sum_{i=1}^{K} N_i = N )\)
那么,总的协整检验次数为:
\[\sum_{i=1}^{K} \binom{N_i}{2} = \sum_{i=1}^{K} \frac{N_i (N_i - 1)}{2}\]
如果每个簇的样本数量大致相同,此时总的协整检验次数就会少不少。比如,如果有 100 支资产,可以聚类成 10 个 size 一样的簇,那么总的协整检验次数就只有\(10 * C_{10}^2\)次,即 450 次,比之前的 4950 次,下降了 90%还多。
hdbscan 聚类
聚类算法有很多种,sklearn 中提到的就有 10 多种。不过,对通用目的而言,最好的聚类算法可能是 hdbscan。它不令速度快(仅次于 kmeans),而且能容忍噪声,并且超参数也很容易理解和设置。
下图是在同一个数据集上,hdbscan, dbscan 和 k-means 聚类的效果对比:
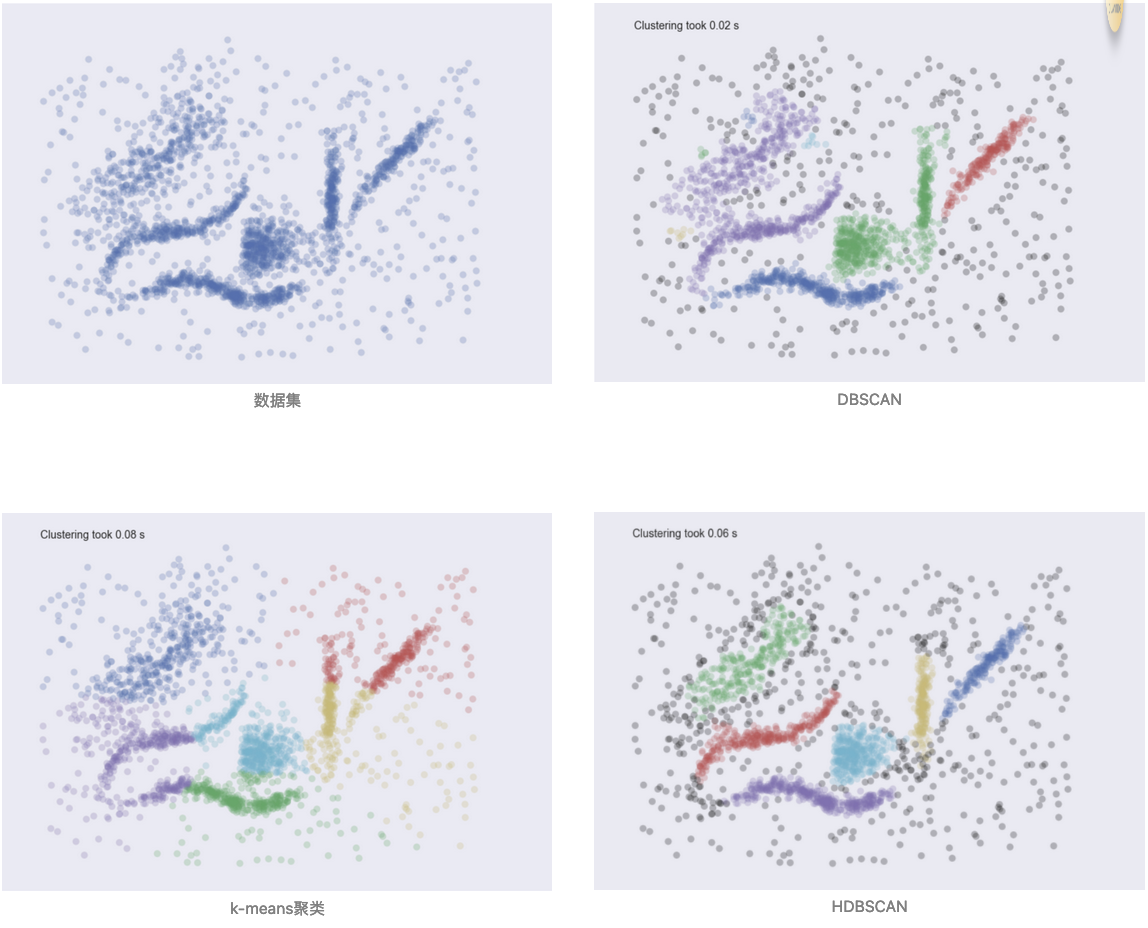
DBSCAN 不能找出比指定的核密度更稀疏的簇;k-means 会把噪声也归划分到距离最近的簇中,并且你得告诉它这个数据集中有多少个簇;hdbscan 的表现几近完美。
接下来,我们就运用 hdbscan 来对资产进行聚类。在聚类完成之后,我们还将对它进行协整检验,并将最终结果可视化展示出来。
1
2
3
4
5
6
7
8
9
10
11
12
13 | import hdbscan
import pandas as pd
from sklearn.manifold import TSNE
import plotly.express as px
start = datetime.date(2022, 1, 1)
end = datetime.date(2023,12,31)
barss = load_bars(start, end, 2000)
closes = (barss["close"].unstack().
ffill().
dropna(axis=1, how='any'))
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | # 使用 HDBSCAN 进行聚类
clusterer = hdbscan.HDBSCAN(min_cluster_size=3, min_samples=2)
cluster_labels = clusterer.fit_predict(closes.T)
# 将聚类结果添加到 DataFrame 中
clustered = closes.T.copy()
clustered['cluster'] = cluster_labels
# 剔除类别为-1 的点,这些是噪声,而不是一个类别
clustered = clustered[clustered['cluster'] != -1]
clustered_close = clustered.drop("cluster", axis=1)
# 使用 t-SNE 进行降维
tsne = TSNE(n_components=3, random_state=42)
tsne_results = tsne.fit_transform(clustered_close)
# 将 t-SNE 结果添加到 DataFrame 中
reduced_tsne = pd.DataFrame(data=tsne_results,
columns=['tsne_1', 'tsne_2', 'tsne_3'],
index=clustered_close.index)
reduced_tsne['cluster'] = clustered['cluster']
fig_tsne = px.scatter_3d(
reduced_tsne,
x='tsne_1', y='tsne_2', z='tsne_3',
color='cluster',
title='t-SNE Clustering of Stock Returns',
labels={'tsne_1': 't-SNE Component 1',
'tsne_2': 't-SNE Component 2'}
)
fig_tsne.layout.width = 1200
fig_tsne.layout.height = 1100
fig_tsne.show()
|
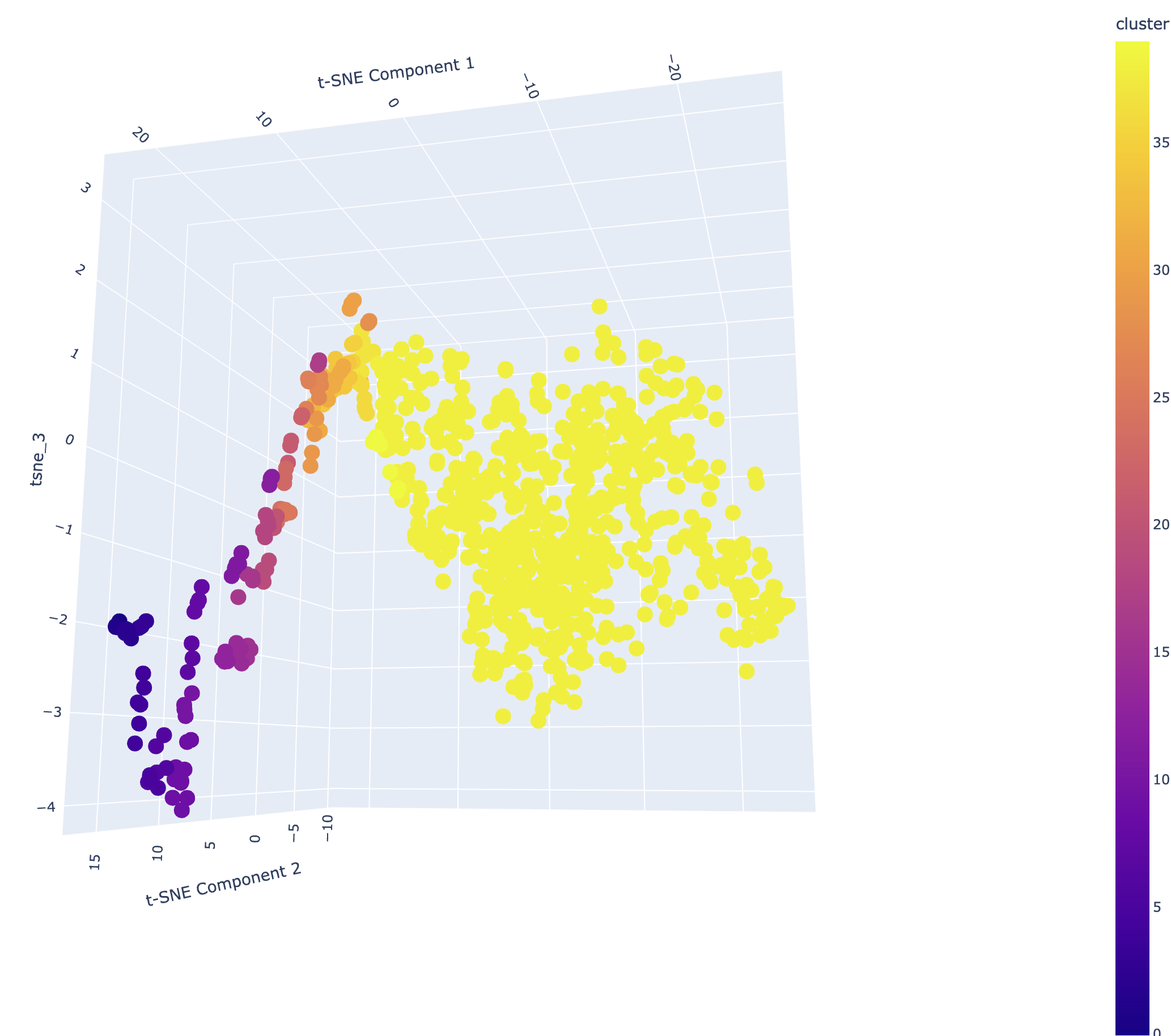
我们将得到一个三维的 t-SNE 图,其中颜色表示每个点的聚类。在我们的研究平台上,你可以运行代码并生成这个三维图,然后拖拽它以变换观察视角。
hdbscan 的聚类效果如何?我们能否在它划分的类别中,寻找到协整对呢?我们通过下面的代码来可视化簇类的样本走势,并执行协整检验。这是随机抽取的第 12 簇的情况:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | from statsmodels.tsa.stattools import coint
import hdbscan
import pandas as pd
from sklearn.manifold import TSNE
import plotly.express as px
start = datetime.date(2022, 1, 1)
end = datetime.date(2023,12,31)
barss = load_bars(start, end, 2000)
closes = barss["close"].unstack().ffill().dropna(axis=1, how='any')
# 使用 HDBSCAN 进行聚类
clusterer = hdbscan.HDBSCAN(min_cluster_size=3, min_samples=2)
cluster_labels = clusterer.fit_predict(closes.T)
clustered = closes.T.copy()
clustered['cluster'] = cluster_labels
# 剔除类别为-1 的点,这些是噪声,而不是一个类别
clustered = clustered[clustered['cluster'] != -1]
clustered_close = clustered.drop("cluster", axis=1)
plt.figure(figsize=(12,10))
cluster_12 = clustered.query("cluster == 12").index.tolist()
for code in cluster_12:
bars = barss.xs(code, level=1)["close"]
plt.plot(bars)
pairs = []
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | for i in range(len(cluster_12)):
for j in range(i + 1, len(cluster_12)):
pair1 = cluster_12[i]
pair2 = cluster_12[j]
price1 = barss.xs(pair1, level=1)["close"].ffill().dropna()
price2 = barss.xs(pair2, level=1)["close"].ffill().dropna()
minlen = min(len(price1), len(price2))
t, p, *_ = coint(price1[-minlen:], price2[-minlen:])
if p < 0.05:
pairs.append((pair1, pair2))
row = max(1, len(pairs) // 3)
col = len(pairs) // row
if row * col < len(pairs):
row += 1
cells = row * col
fig, axes = plt.subplots(row, col, figsize=(col * 3,row * 3))
axes = np.array(axes).flatten()
fig.suptitle('Cointegrated Pairs')
plot_index = 0
for pair1, pair2 in pairs:
ax = axes[plot_index]
price1 = barss.xs(pair1, level=1)["close"]
price2 = barss.xs(pair2, level=1)["close"]
ax.plot(price1, label=pair1)
ax.plot(price2, label=pair2)
ax.set_title(f'{pair1[:-5]} & {pair2[:-5]}')
ax.set_xticks([])
plot_index += 1
plt.tight_layout()
plt.show()
print(len(pairs)/(len(cluster_12) * (len(cluster_12) - 1)) * 2)
|
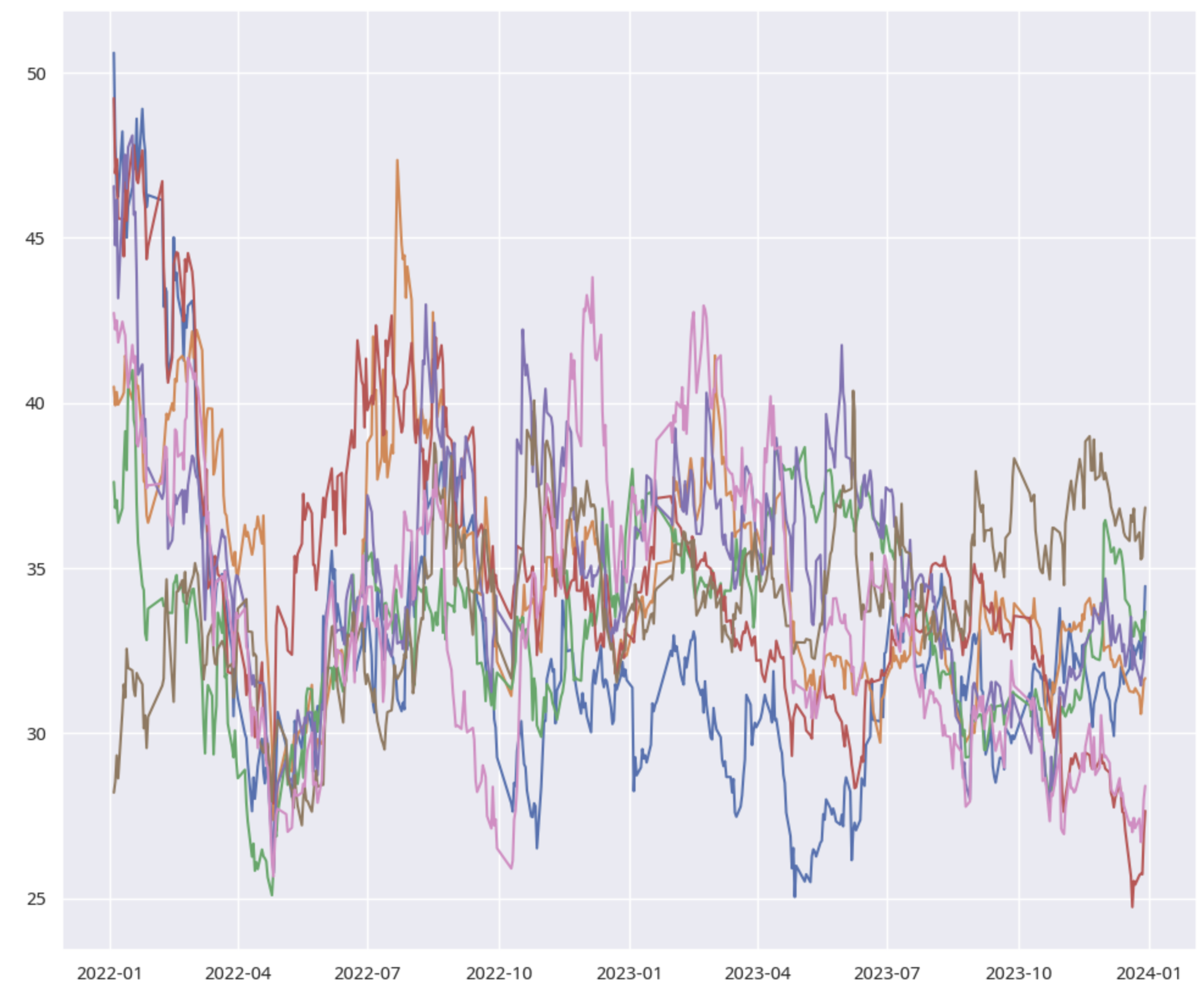
从结果可以看出,簇类的个股走势几乎一样,但不是簇内所有的组合都是协整对。这也很容易理解,毕竟,**聚类有聚类的逻辑,协整又是协整的逻辑**。两者有重叠的空间,但决不是一码事儿。
重要的是,我们大大压缩了计算时间。叹隙中驹,石中火,梦中身,但现在,只在白驹隙的这一瞬,我们就发现了新的财富密码。抢先在量化中是极其重要的,一旦机会被其他人也找到,有限的资金容量就会被他人抢走。
## 摇人!赶快摇人!
匡醍科技 (Quantide) 新年开始,要招人啦!我们在各个招聘平台发了英雄贴,不过,最契合的候选人很可能应该来自于公众号的粉丝。如果你喜欢我的文章,也可能喜欢跟我一起工作,一起探索量化交易。
在匡醍,我们一边研究(量化框架研发、交易策略),一边产出(通过公众号或者视频号),永远在成长,费曼学习法。毕竟,量化研究就象西西弗斯,你每天滚石上山,但没有一劳永逸的成功,只有日复一日的失败、学习和再次出发!
具体地说,这个职位有以下非(脱敏)典型症状,精通量化所需要的概率、统计知识,熟练掌握 Python 和 numpy, pandas,statsmodels, scipy, 机器学习算法,文字爱好者,会修图,懂 AI,新概念、新技术的 super fans。妥妥的六边形战士。不过,不管你是三角形还是正方形,只要真正的热爱这样的工作,都可以来撩。我现在最想要的,是一个学习博主,真真正正学习的那种,不是只摆个 pose 的那种。
_具体岗位请致电
[email protected] 查询,或者直接空投简历,在校生可投实习岗位_

热爱是最好的老师。在宇宙中心等你。
 农齐奥.塔尔塔里亚
农齐奥.塔尔塔里亚