跳转至

Numpy处理表格数据

一开始，Numpy 的数组只能存放同质的元素，即元素必须有相同的数据类型。但对表格类数据而言，它们往往是由一条条记录组成的，而这些记录，又是由不同数据类型的数据组成的。

如何做到在Numpy中也能处理大规模的表格数据呢？

1. Structured Array

为了满足这种需求，Numpy 扩展出一种名为 Structured Array 的数据格式。它是一种 一维数组，每一个元素都是一个命名元组。

我们可以这样声明一个 Structured Array:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
import numpy as np
import datetime
dtypes = [
        ("frame", "O"),
        ("code", "O"),
        ("open", "f4"),
        ("high", "f4"),
        ("low", "f4"),
        ("close", "f4")
    ]
secs = np.array (
    [
        (datetime.date (2024, 3, 18), "600000", 8.9, 9.1, 8.8, 9),
        (datetime.date (2024, 3, 19), "600000", 8.9, 9.1, 8.8, 9),
    ], dtype = dtypes
)

在这个数据结构中，共有 6 个字段，它们的名字和类型通过 dtype 来定义。这是一个 List [Tuple] 类型。在初始化数据部分，它也是一个 List [Tuple]。

Warning

初学者很容易犯的一个错误，就是使用 List [List] 来初始化 Numpy Structured Array，而不是 List [Tuple] 类型。这会导致 Numpy 在构造数组时，对应不到正确的数据类型，报出一些很奇怪的错误。
比如，下面的初始化是错误的：

1
2
3
4
secs = np.array ([
    [datetime.date (2024, 3, 18), "600000", 8.9, 9.1, 8.8, 9],
    [datetime.date (2024, 3, 19), "600000", 8.9, 9.1, 8.8, 9]
], dtype=dtypes)
这段代码会报告一个难懂的 "Type Error: float () argument must be a string or ..."

我们使用上一节学过的 inspecting 方法来查看 secs 数组的一些特性:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
print (f"secs 的维度是 {secs.ndim}")
print (f"secs 的 shape 是 {secs.shape}")
print (f"secs 的 size 是 {secs.size}")
print (f"secs 的 length 是 {len (secs)}")

print (f"secs [0] 的类型是 {type (secs [0])}")
print (f"secs [0] 的维度是 {secs [0].ndim}")
print (f"secs [0] 的 shape 是 {secs [0].shape}")
print (f"secs [0] 的 size 是 {secs [0].size}")
print (f"secs [0] 的 length 是 {len (secs [0])}")

可以看出，secs 数组是 一维数组，它的 shape (2,) 也正是一维数组的 shape 的表示法。前一节还介绍过这几个属性的关系，大家可以自行验证下是否仍然得到满足。

Tip

这里 size 仍然等于 shape 各元素的取值之积。注意对 secs 而言，它的 size 与 length 是相等的，但对 secs [0] 而言，它的 size 和 length 是不相等的。我们在开发 Zillionare 量化框架时时，遇到过由此产生的一个 bug。

但 secs 的元素类型则是 numpy.void，它在本质上是一个 named tuple，所以，我们可以这样访问其中的任一字段：

1
2
3
4
print (secs [0]["frame"])

# 不使用列名（字段名），使用其序号也是可以的
print (secs [0][0])

我们还可以以列优先的顺序来访问其中的一个 “单元格”：

1
print (secs ["frame"][0])

对表格数据，遍历是很常见的操作，我们可以这样遍历：

1
2
for (frame, code, opn, high, low, close) in secs:
    print (frame, code, opn, high, low, close)

Numpy structured array 在这部分的语法要比 Pandas 的 DataFrame 易用许多。我们在后面介绍 Pandas 时，还会提及这一点。

Warning

修改 cell 值时，索引的先后不能互换： 

1
2
3
4
5
6
7
8
    data = np.array ([("aaron", "label")], dtype=[("name", "O"), ("label", "O")])
    filter = data ["name"] == "aaron"

    new_label = "blogger"
    data ["label"][filter] = new_label

    # this won't change
    data [filter]["label"] = new_label
这里的最后一行，并不会生效。

2. 运算类

2.1. 比较和逻辑运算

我们在上一节介绍定位、查找时，已经接触到了数据比较，比如:arr > 1。它的结果将数组中的每一个元素都与 1 进行比较，并且返回一个布尔型的数组。

现在，我们要扩充比较的指令：

函数 描述
all 如果数组中的元素全为真，返回 True。可用以判断一组条件是否同时成立。
any 如果数组中至少有一个元素为真，则返回 True。用以判断一组条件是否至少有一个成立
isclose 判断两个数组中的元素是否一一近似相等，返回所有的比较结果
allclose 判断两个数组中的元素是否全部近似相等
函数 描述
equal 判断两个数组中的元素是否一一相等，返回所有的比较结果。
not_equal 一一判断两个数组中的元素是否不相等，返回所有的比较结果
isfinite 是否为数字且不为无限大
isnan 测试是否为非数字
isnat 测试对象是否不为时间类型
isneginf 测试对象是否为负无限大
isposinf 测试对象是否为正无限大 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
# 开启多行输出模式
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

np.random.seed (78)
returns = np.random.normal (0, 0.03, size=4)
returns
# 判断是否全下跌
np.all (returns <= 0)
np.any (returns <= 0)

# 模拟一个起始价格为 8 元的价格序列
prices = np.cumprod (1+returns) * 8

# 对应的涨停价如下
buy_limit_prices = [8.03, 8.1, 8.1, 8.3]

# 判断是否涨停
np.isclose (prices, buy_limit_prices, atol=1e-2)

Tip

为什么需要存在判断近似相等的函数？这是因为，数字分为整型和浮点型。凡是带小数点的数字，都可以看成浮点型。许多浮点数不能精确表达，所以它们是不会相等的，只能比较两个浮点数的差值，如果差值的绝对值小于某个可以接受的小数，才能认为这两个数近似相等。

因此，如果我们拿到了个股的收盘价和涨停价，要判断此时个股有没有涨停，就只能用 isclose 来进行比较，而不能使用 equal。

参数 atol 表示绝对误差，表示两个浮点数之间的差值小于这个值，就可以认为这两个数近似相等。

除了判断一个数组中的元素要么都为 True，要么至少一个为 True 之外，有时候我们还希望进行模糊一点的判断，比如，如果过去 20 天中，超过 60% 的是收阳线，此时我们可以用 np.count_nonzero，或者 np.sum 来统计数组中为真的情况：

1
2
np.count_nonzero (returns > 0)
np.sum (returns > 0)

在上一节进行比较的示例中，我们都只使用了单个条件。如果我们要按多个条件的组合进行查找，就需要依靠逻辑运算来实现。

在 Numpy 中，逻辑运算既可以通过函数、也可以通过运算符来完成：

函数 运算符 描述 python 等价物
logical_and & 执行逻辑与操作 and
logical_or | 执行逻辑或操作 or
logical_not ~ 执行逻辑或操作 not
logical_xor '^' 执行逻辑异或操作 xor

Tip

如果你对编程语言不是特别熟悉，就会难以理解这里的布尔运算，但它们在量化中运用非常广泛，并且在后面讲 pandas 时，我们还会遇到

逻辑与 a&b 的含义是， 只有当条件 a 与 b 都为真时，表达式才成立 逻辑或 a|b 的含义是，a 与 b 之中，任何一个为真即成立 逻辑非～b 的含义是，如果 b 为真，则表达式不成立，反之则成立 逻辑异或 a ^ b 的含义是，只有两个不同时才为真。

逻辑运算有什么用呢？比如我们在选股时，有以下表格数据：

股票 pe mom
AAPL 30.5 0.1
GOOG 32.3 0.3
TSLA 900.1 0.5
MSFT 35.6 0.05

上述表格可以用 Numpy 的 Structured Array 来表示为：

1
2
3
4
5
6
tickers = np.array ([
    ("APPL", 30.5, 0.1),
    ("GOOG", 32.3, 0.3),
    ("TSLA", 900.1, 0.5),
    ("MSFT", 35.6, 0.05)
], dtype=[("ticker", "O"), ("pe", "f4"), ("mom", "f4")])

现在，我们要找出求 PE < 35, 动量 (mom) > 0.2 的记录，那么我们可以这样构建条件表达式：

1
(tickers ["pe"] < 35) & (tickers ["mom"] > 0.2)

Numpy 会把 pe 这一列的所有值跟 35 进行比较，然后再与 mom 与 0.2 比较的结果进行逻辑与运算，这相当于：

1
np.array ((1,1,0,0)) & np.array ((0, 1, 1, 0))

在 Numpy 中，True 与 1 的值在做逻辑运算时是相等的；0 与 False 也是。

如果不借助于 Numpy 的逻辑操作，我们就要用 Python 的逻辑操作。很不幸，这必须使用循环。如果计算量大，这将会比较耗时间。

Tip

这里解释下异或操作。它比较拧巴。如果两个操作数取值一样，那么结果为 False；否则为 True，非常不团结。

在量化中使用异或操作的例子仍然最可能来自于选股。比如，如果我们要求两个选股条件，只能有一个成立时，才买入；否则不买入，就可以使用异或运算。

Tip

在多个条件中，投资者为什么会想要只有一个条件成立？这可能是因为他们认为这两个条件可能互相冲突，或者他们想要在两种投资策略之间进行平衡。

2.2. 集合运算

在交易中，我们常常要执行调仓操作。做法一般是，选确定新的投资组合，然后与当前的投资组合进行比较，找出需要卖出的股票，以及需要买入的股票。这个操作，就是集合运算。在 Python 中，我们一般是通过 set 语法来实现。

在 Numpy 中，我们可以使用通过以下方法来实现集合运算： 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
import numpy as np

# 创建两个一维数组
x = np.array ([1, 2, 3, 4, 5])
y = np.array ([4, 5, 6, 7, 8])

# 计算交集
intersection = np.intersect1d (x, y)
print ("Intersection (交集):", intersection)

# 计算并集
union = np.union1d (x, y)
print ("Union (并集):", union)

diff = np.setdiff1d (x, y)
print ("x - y:", diff)

此外，我们还可能使用 in1d (a1, a2) 方法来判断 a1 中的元素是否都在 a2 中存在。比如，在调仓换股中，如果当前持仓都在买入计划中，则不需要执行调仓。

2.3. 数学运算和统计

Numpy 中数学相关的运算有线性代数运算（当然还有基本代数运算）、统计运算、金融指标运算等等。

2.3.1. 线性代数

线性代数在量化中有重要用途。比如，在现代资产组合理论（MPT）中，我们要计算资产组合收益率及协方差，都要使用矩阵乘法。大家可以参考 投资组合理论与实战 系列文章，下面是其中的一段代码：

1
2
3
...
cov = np.cov (port_returns.T)
port_vol = np.sqrt (np.dot (np.dot (weights, cov), weights.T))

矩阵乘法是线性代数中的一个核心概念，它涉及到两个矩阵的特定元素按照规则相乘并求和，以生成一个新的矩阵。具体来说，如果有一个矩阵 A 为 \(m \times n\) 维，另一个矩阵 B 为 \(n \times p\) 维，那么它们的乘积 \(C = AB\) 将会是一个 \(m \times p\) 维的矩阵。乘法的规则是 A 的每一行与 B 的每一列对应元素相乘后求和。

下面通过一个具体的例子来说明矩阵乘法的过程：

假设我们有两个矩阵 A 和 B：

$$ A = \begin {bmatrix} 2 & 3 \ 1 & 4 \end {bmatrix} $$ 和 $$ B = \begin {bmatrix} 1 & 2 \ 3 & 1 \end {bmatrix} $$ 要计算 AB，我们遵循以下步骤：

取 A 的第一行 \((2, 3)\) 与的第一列 \((1,3)\) 相乘并求和得到 \(C_{11} = [2\times1 + 3\times3 = 11]\)

同理，取 A 的第一行与 B 的第二列 \((2, 1)\) 相乘并求和得到 \(C_{12} = [2\times2 + 3\times1 = 7]\)

取 A 的第二行 \((1, 4)\) 与 B 的第一列相乘并求和得到 \(C_{21} = [1\times1 + 4\times3 = 13]\)

取 A 的第二行与 B 的第二列相乘并求和得到 \(C_{22} = [1\times2 + 4\times1 = 5]\)

因此，矩阵 C = AB 为：

\[ C = \begin {bmatrix} 11 & 7 \\ 13 & 6 \ \end {bmatrix} \]

与代数运算不同，矩阵乘法不满足交换律，即一般情况下 \(AB \neq BA\)。

在 Numpy 中，我们可以使用 np.dot () 函数来计算矩阵乘法。

上述示例使用 numpy 来表示，即为：

1
2
3
4
A = np.array ([[2,3],[1,4]])
B = np.array ([[1,2],[3,1]])

np.dot (A, B)

最终我们将得到与矩阵 C 相同的结果。

除此之外，矩阵逆运算 (np.linalg.inv) 在计算最优投资组合权重时，用于求解方程组，特征值和特征向量 (np.linalg.eig, np.linalg.svd) 在分析资产回报率的主成分，进行风险分解时使用。

2.3.2. 统计运算

常用的统计运算包括：

函数 描述
np.mean 计算平均值
np.median 计算中位数
np.std 计算标准差
np.var 计算方差
np.min 计算最小值
np.max 计算最大值
np.percentile 用于计算历史数据的分位点
np.quantile 用于计算历史数据的分位数，此函数与 percentile 功能相同
np.corr 用于计算两个变量之间的相关性

np.percentile 与 np.quantile 功能相同，都是用于计算分位数。

两者在参数上略有区别。当我们对同一数组，给 quantile 传入分位点 0.25 时，如果给 percentile 传入分位点 25 时，两者的结果将完全一样。也就是后者要乘以 100。在量化交易中，quantile 用得可能会多一些。

Tip

在 pandas 中存在 quantile 函数，但没有 percentile 函数。

np.percentile（或者 np.quantile）的常见应用是计算 25%, 50% 和 75% 的分位数。用来绘制箱线图（Boxplot）。

此外，我们也常用它来选择自适应参数。比如，在 RSI 的应用中，一般推荐是低于 20（或者 30）作为超卖，此时建议买入；推荐是高于 80（或者 70）作为超买，此时建议卖出。但稍微进行一些统计分析，你就会发现这些阈值并不是固定的。如果我们以过去一段时间的 RSI 作为统计，找出它的 95% 分位作为卖点，15% 作为买点，往往能得到更好的结果。

2.3.3. 量化指标的计算

有一些常用的量化指标的计算，也可以使用 Numpy 来完成，比如，计算移动平均线，就可以使用 Numpy 提供的 convolve 函数。

1
2
3
4
5
import numpy as np
def moving_average (data, window_size):
    return np.convolve(data,
                       np.ones(window_size)/window_size, 
                       'valid')

当然，很多人习惯使用 talib，或者 pandas 的 rolling 函数来进行计算。convolve（卷积）是神经网络 CNN 的核心，正是这个原因，我们这里提一下。

np.convolve 的第二个参数，就是卷积核。这里我们是实现的是简单移动平均，所以，卷积核就是一个由相同的数值组成的数组，它们的长度就是窗口大小，它们的和为 1。

如果我们把卷积核替换成其它值，还可以实现 WMA 等指标。从信号处理的角度看，移动平均是信号平滑的一种，使用不同的卷积核，就可以实现不同的平滑效果。

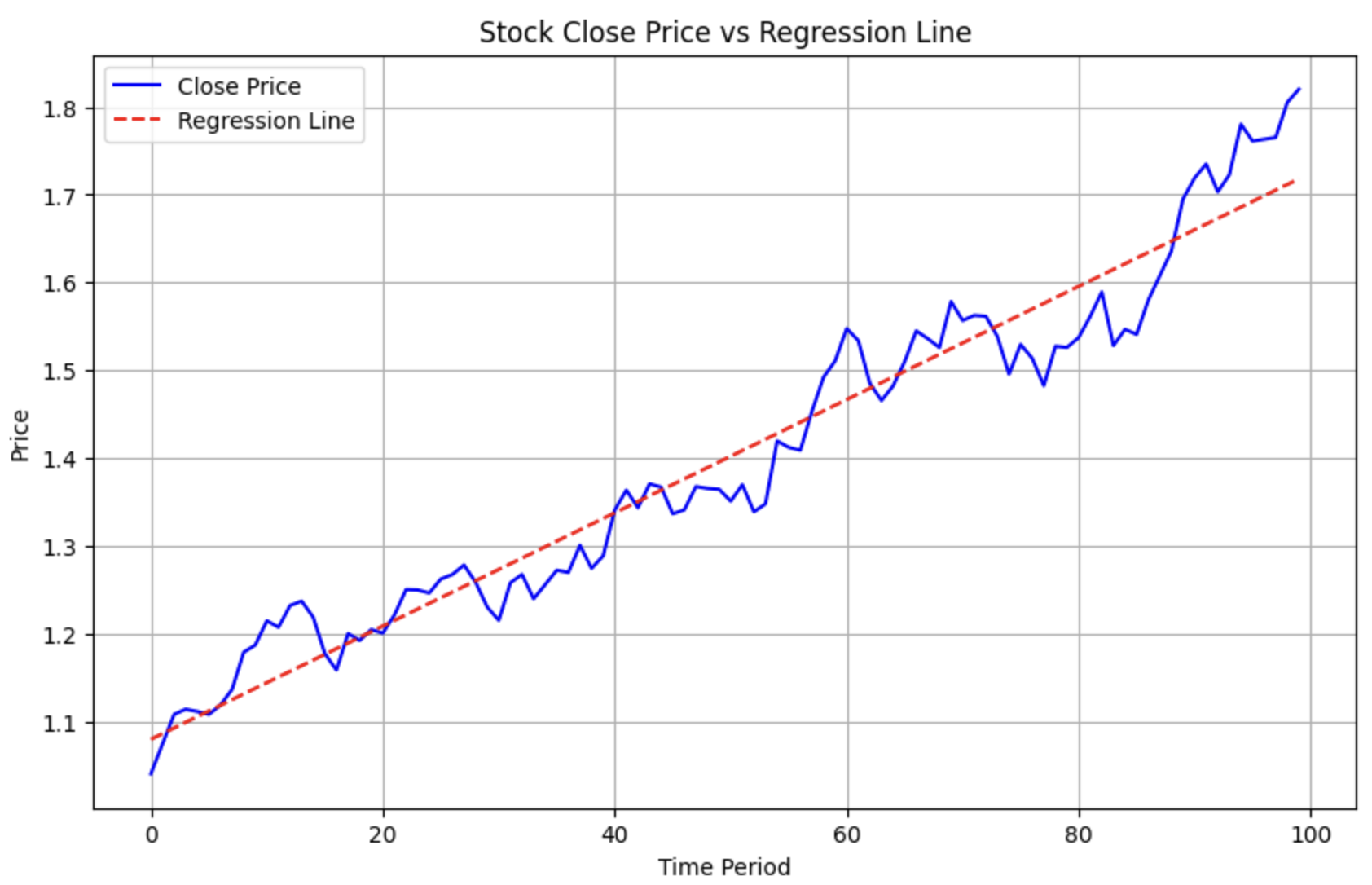
在量化中，还有一类计算，这里也提一下，就是多项式回归。比如，某两支股票近期都呈上升趋势，我们想知道哪一支涨得更好？这时候我们就可以进行多项式回归，将其拟合成一条直线，再比较它们的斜率。

下面的代码演示了如何使用 Numpy 进行多项式回归。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
import numpy as np
import matplotlib.pyplot as plt

returns = np.random.normal (0, 0.02, size=100)
alpha = 0.01
close = np.cumprod (1 + returns + alpha)

a, b = np.polyfit (np.arange (100), close, deg=1)

# 使用 a, b 构建回归线的 y 值
regression_line = a * np.arange (100) + b

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
# 绘制原始的 close 曲线
plt.figure (figsize=(10, 6))
plt.plot (close, label='Close Price', color='blue')

# 绘制回归线
plt.plot (regression_line, label='Regression Line', color='red', linestyle='--')

# 添加图例、标题和坐标轴标签
plt.title ('Stock Close Price vs Regression Line')
plt.xlabel ('Time Period')
plt.ylabel ('Price')
plt.legend ()

# 显示图表
plt.grid (True)
plt.show ()

这将生成下图：

题图： Photo by Steve Harvey on Unsplash