跳转至

Numpy核心语法[4]

“随机数和采样是量化中的高频操作。通过 Numpy 的 random 模块，我们可以轻松生成符合正态分布的收益率数组，并利用 np.cumprod() 计算价格走势，快速模拟资产的夏普率与价格关系。”

1. 随机数和采样

随机数和采样是量化中的高频使用的操作。在造数据方面非常好用。我们在前面的示例中，已经使用过了 normal() 函数，它是来自 numpy.random 模块下的一个重要函数。借由这个函数，我们就能生成随机波动、但总体上来看又是上涨、下跌或者震荡的价格序列。

Tip

我们会在何时需要造价格序列？除了前面讲过的例子外，这里再举一例：我们想知道夏普为\(S\)的资产，它的价格走势是怎么样的？价格走势与夏普的关系如何？要回答这个问题，我们只能使用“蒙”特卡洛方法，造出若干模拟数据，然后计算其夏普并绘图。此时我们一般选造一个符合正态分布的收益率数组，然后对它进行加权（此时即可算出夏普），最后通过 np.cumprod() 函数计算出价格走势，进行绘图。

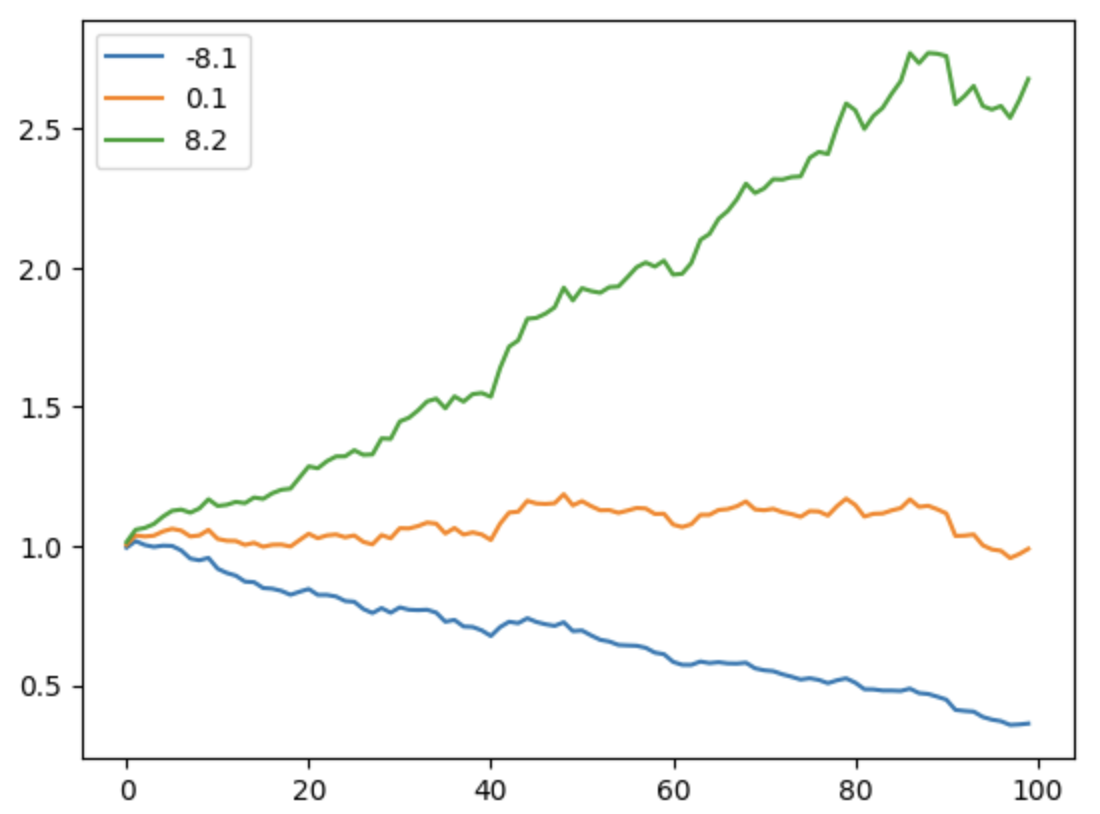
我们通过一个例子来说明夏普与股价走势之间的关系：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
import numpy as np
from empyrical import sharpe_ratio
import matplotlib.pyplot as plt

returns_ = np.random.normal(0, 0.02, size=100)
legend = []

for alpha in (-0.01, 0, 0.01):
    returns = returns_ + alpha
    prices = np.cumprod(returns + 1)
    sharpe = sharpe_ratio(returns)
    _ = plt.plot(prices)
    legend.append(f"{sharpe:.1f}")

1
2
lines = plt.gca().lines
plt.legend(lines, legend)

从绘制的图形可以看出，当 alpha 为 1%时，夏普率可达 8.2。国内优秀的基金经理可以在一年内，做到 2~3 左右的夏普率。大家可以调整 alpha 这个参数，看看 alpha 与夏普率的关系。

50%

1.1. The legacy: np.random module

迄今为止，我们在网上看到的多数关于 numpy random 的教程，都是使用的 np.random module 下面的函数。除了 normal 方法之外，random 包中还有以下函数：

函数 说明
randint(a,b,shape) 生成在区间 (a,b) 之间，形状为 shape 的随机整数数组。
rand(shape) 生成 shape 形状的随机数组，使用 [0,1) 区间的均匀分布来填充。
random(shape) 生成 shape 形状的随机数组，使用均匀分布填充
randn(d1, d2, ...) 生成 shape 形状的随机数组，使用正态分布来填充。
standard_normal(shape) 生成 shape 形状的随机数组，使用标准正态分布来填充。
函数 说明
normal(loc,scale,shape) 生成 shape 形状的随机数组，使用正态分布来填充，loc 是均值，scale 是标准差。
choice(a,size,replace,p) 从 a 中随机抽取 size 个元素，如果 replace=True, 则允许重复抽取，否则不允许重复抽取。p 表示概率，如果 p=None, 则表示每个元素等概率抽取。
shuffle(a) 将 a 中的元素随机打乱。
seed(seed) 设置随机数种子，如果 seed=None, 则表示使用系统时间作为随机数种子。

可以看出，numpy 为使用同一个功能，往往提供了多个方法。我们记忆这些方法，首先是看生成的随机数分布。最朴素的分布往往有最朴素的名字，比如，rand, randint 和 random 都用来生成均匀分布，而 normal, standard_normal 和 randn 用来生成正态分布。

除了均匀分布之外，Numpy 还提供了许多著名的分布的生成函数，比如 f 分布、gama 分布、hypergeometric（超几何分布），beta, weibull 等等。

在同一类别中，numpy 为什么还要提供多个函数呢？有一些是为了方便那些曾经使用其它知名库（比如 matlab) 的人而提供的。

randn 就是这样的例子，它是 matlab 中一个生成正态随机分布的函数，现在被 numpy 移植过来了。我们这里看到的另一个函数，rand 也是这样。而对应的 random，则是 Numpy 按自己的 API 风格定义的函数。

choice 方法在量化中有比较具体的应用。比如，我们可能想要从一个大的股票池中，随机抽取 10 只股票先进行一个小的试验，然后根据结果，再考虑抽取更多的股票。

seed 函数用来设置随机数生成器的种子。在进行单元测试，或者进行演示时（这两种情况下，我们都需要始终生成相同的随机数序列）非常有用。

1.2. New Style: default_rng

我们在上一节介绍了一些随机数生成函数，但没有介绍它的原理。Numpy 生成的随机数是伪随机数，它们是使用一个随机数生成器（RNG）来生成的。RNG 的输出是随机的，但是相同的输入总是会生成相同的输出。我们调用的每一个方法，实际上是在这个序列上的一个抽取动作（根据输入的 size/shape）。

在 numpy.random 模块中，存在一个全局的 RNG。在我们调用具体的随机函数时，实际上是通过这个全局的 RNG 来产生随机数的。而这个全局的 RNG，总会有人在它之上调用 seed 方法来初始化。这会产生一些问题，因为你不清楚何时、在何地、以哪个参数被人重置了 seed。

由于这个原因，现在已经不推荐直接使用 numpy.random 模块中的这些方法了。更好的方法是，为每一个具体地应用创建一个独立的 RNG，然后在这个对象上，调用相应的方法：

1
2
rng = np.random.default_rng(seed=123)
rng.random(size=10)

rng 是一个 Random Generator 对象，在初始化时，我们需要给它传入一个种子。如果省略，那么 Numpy 会使用系统时间作为种子。

rng 拥有大多数前一节中提到的方法，比如 normal, f, gamma 等；但从 matlab 中移植过来的方法不再出现在这个对象上。另外，randint 被 rng.integers 替代。

除此之外，default_rng 产生的随机数生成器对象，在算法上采用了 PCG64 算法，与之前版本采用的算法相比，它不仅能返回统计上更好的随机数，而且速度上也会快 4 倍。

Warning

在 numpy 中还存在一个 RandomState 类。它使用了较慢的梅森扭曲器生成伪随机数。现在，这个类已经过时，不再推荐使用。

1.3. 数据集平衡示例

我们已经介绍了 choice 的功能，现在我们来举一个例子，如何使用 choice 来平衡数据集。

在监督学习中，我们常常遇到数据不平衡的问题，比如，我们希望训练一个分类器，但是训练集的类别分布不均衡。我们可以通过 choice 方法对数据集进行 under sampling 或者 over sampling 来解决这个问题。

为了便于理解，我们先生成一个不平衡的训练数据集。这个数据集共有 3 列，其中前两列是特征（你可以想像成因子特征），第三列则是标签。

1
2
3
4
5
6
import pandas as pd
import numpy as np

rng = np.random.default_rng(seed=42)
x = rng.random((10,3))
x[:,-1] = rng.choice([0,1], len(x), p=[0.2, 0.8])

我们通过下面的方法对这个数据集进行可视化，以验证它确实是一个不平衡的数据集。

1
2
df = pd.DataFrame(x, columns=['factor1', 'factor2', 'label'])
df.label.value_counts().plot(kind='bar')

运行结果为：

50%

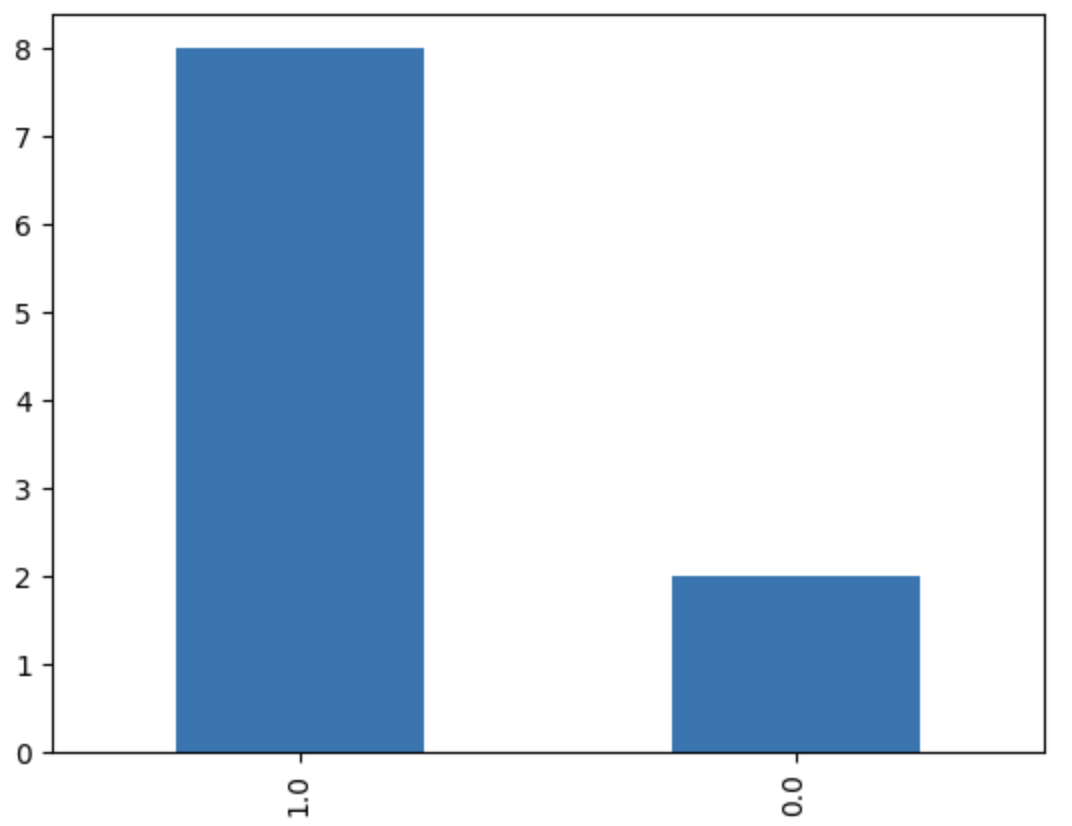
要在此基础上，得到一个新的平衡数据集，我们有两种思路，一种是 under sampling，即从多数类的数据中抽取部分数据，使得它与最小分类的数目相等；另一种是 over sampling，即从少数类的数据中复制部分数据，使得它与最大的类的数目相等。

下面的例子演示了如何进行 under sampling:

1
labels, counts = np.unique(x[:,-1], return_counts=True)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
# 最小分类的标签
min_label = labels[np.argmin(counts)]

# 最小分类样本的数量，作为 UNDER SAMPLING 的样本数量
min_label_count = np.min(counts)

# 最小分类无须抽取，全部提取
results = [
    x[x[:,-1] == min_label]
]

# 对其它分类标签进行遍历，需要先剔除最小分类
for label in np.delete(labels, np.argmin(counts)):
    sampled = rng.choice(x[x[:,-1]== label], min_label_count)
    results.append(sampled)

np.concatenate(results)

这段代码先是找到最小分类及它的数量，然后遍历每个标签，再通过 rng.choice 对其它分类随机抽取最小分类的数量，最后把所有的子集拼接起来。

这段示例代码可用以多个标签的情况。如果要进行 over sampling，只要把其中的 min 换成 max 就可以了。

2. IO 操作

我们直接使用 Numpy 读写文件的场合并不多。提高 IO 读写性能一直都不是 Numpy 的重点，我们也只需要稍加了解即可。

2.1. 读写 CSV 文件

Numpy 可以从 CSV 格式的文本文件中读取数据，主要有以下方法：

api 描述
loadtxt 解析文本格式的表格数据
savetxt 将数据保存为文本文件
genfromtxt 同上，但允许数据中有缺失值，提供了更高级的用法
recfromtxt 是 genfromtxt 的快捷方式，自动推断为 record array
recfromcsv 同上，如果分隔符为逗号，无须额外指定

我们通过下面的示例简单演示一下各自的用法：

1
2
3
4
5
6
7
import io
import numpy 

buffer = io.StringIO("""1,2""")

# 默认情况下，LOADTXT 只能读取浮点数
numpy.loadtxt(buffer, delimiter=",")

这会输出数组array([1., 2.])。

1
2
3
4
buffer = io.StringIO("""1,2,hello""")

# 通过指定 DTYPE 参数，可以读取其它类型
numpy.loadtxt(buffer, delimiter=",", dtype=[("age", "i4"), ("score", "f4"), ("name", "U8")])

这样我们将得到一个 Structured Array，其中第三列为字符串类型。如果我们不指定 dtype 参数，那么 loadtxt 将会解析失败。

1
2
3
4
buffer = io.StringIO("""
1,2,hello
""")
numpy.genfromtxt(buffer, delimiter=",")

这一次我们使用了 genfromtxt 来加载数据，但没有指定 dtype 参数，genfromtxt 会将非数字列解析为 nan。因此，这段代码将输出：`array([1., 2., nan])

现在，我们也给 genfromtxt 加上 dtype 参数：

1
2
3
buffer = io.StringIO("""1,2,hello""")

numpy.genfromtxt(buffer, delimiter=",", dtype=[("age", "i4"), ("score", "f4"), ("name", "U8")])

此时我们得到的结果是：array((1, 2., 'hello'), dtype=[('age', '<i4'), ('score', '<f4'), ('name', '<U8')])。注意它是 Structured Array。

recfromtxt 则不需要 dtype, 会自动推断数据类型。

1
2
3
buffer = io.StringIO("""1,2,hello""")

numpy.recfromtxt(buffer,delimiter=",")

这段代码输出为rec.array((1, 2, b'hello'), dtype=[('f0', '<i8'), ('f1', '<i8'), ('f2', 'S5')])。如果推断不准确，我们也可以自己加上 dtype 参数。

如果我们使用 recfromcsv，则连 delimiter 参数都可以省掉。

1
2
buffer = io.StringIO("""age,score,name1,2,hello""")
numpy.recfromcsv(buffer)

输出跟上一例的结果一样。

出于速度考虑，我们还可以使用其它库来解析 CSV 文件，再转换成为 numpy 数组。比如：

1
2
3
4
5
# 利用 CSV.READER() 来解析，比 NUMPY 快 8 倍
np.asarray(list(csv.reader()))

# 利用 PANDAS 来解析，比 NUMPY 快 22 倍
pd.read_csv(buffer).to_records()

2.2. 读写二进制文件

如果我们不需要与外界交换数据，数据都是自产自销型的，也可以使用二进制文件来保存数据。

使用 numpy.save 函数来将单个数组保存数据为二进制文件，使用 numpy.load 函数来读取 numpy.save 保存的数据。这样保存的文件，文件扩展名为.npy。

如果要保存多个数组，则可以使用 savez 命令。这样保存的文件，文件扩展名为.npz。如果有更复杂的需求，可以使用 Hdf5，pyarrow 等库来进行保存数据。