跳转至

Numpy核心语法[6]

“Masked Array 是 Numpy 中的重要概念，能帮助我们在保持数据完整性的同时，屏蔽无效值进行运算。而 ufunc 则通过底层 C 实现的向量化操作，让复杂计算变得高效且简洁。”

1. Masked Array

你可能常常在一些接近底层的库中，看到 Numpy masked array 的用法。Masked Array 是 Numpy 中很重要的概念。考虑这样的情景，你有一个数据集，其中包含了一些缺失的数据或者无效值。这些”不合格“的数据，可能以 np.nan，np.inf, None 或者其它仅仅是语法上有效的值来表示（比如，在 COVID-19 数据集中，病例数出现负数）的。如何在保持数据集的完整性不变的前提下，仍然能对数据进行运算呢？

Note

这里有一个真实的例子。你可以在 Kaggle 上找到一个 COVID-19 的数据集，这个数据集中，就包含了累积病例数为负数的情况。该数据集由 Johns Hoopkins University 收集并提供。

很显然，我们无法直接对这些数据进行运算。请看下面的例子：

1
2
3
x = np.array([1, 2, 3, np.inf, np.nan, None])
np.mean(x)
np.nanmean(x)

只要数据中包含 np.nan, np.inf 或者 None，numpy 的函数就无法处理它们。即使数据在语法上合法，但在语义上无效，Numpy 强行进行计算，结果也是错误的。

这里有一个量化中可能遇到的真实场景，某公司有一年的年利润为零，这样使得它的 YoY 利润增长在次年变得无法计算。如果我们需要利用 YoY 数据进一步进行运算，我们就需要屏蔽这一年的无效值。否则，我们会连 YoY 利润的均值都无法计算出来。

这里有一个补救的方法，就是将原数据拷贝一份，并且将无效值替换为 np.nan。此后多数运算，都可以用np.nan*来计算。这个方法我们已经介绍过了。但是，如果你是原始数据的收集者，显然你应该照原样发布数据，任何修改都是不合适的；如果你是数据的应用者，当然应该对数据进行预处理后，才开始运算。但是，你又很可能缺少了对数据进行预处理所必须的信息 -- 你怎么能想到像-1, 0 这样看起来人畜无害的小可爱们，竟然是隐藏着的错误呢？

为了解决这个问题，Numpy 就提供了 Masked Array。但是我们不打算在 Masked Array 上过多着墨。关于 Masked Array，我们可以借用这样一句话，很多人不需要知道 Masked Array，知道 Masked Array 的人则已经精通它了。

有一点需要注意的是，仅在需要时，使用 Masked Array。因为可能与您相像的相反，Masked Array 不会提高性能，反而，它大大降低了性能：

1
2
3
4
5
6
7
8
import numpy as np

# NUMPY VERSION 1.24.4
g = np.random.random((5000,5000))
indx = np.random.randint(0,4999,(500,2))
g_nan = g.copy()
g_nan[indx] = np.nan
mask =  np.full((5000,5000),False,dtype=bool)

1
2
3
4
5
6
7
mask[indx] = True
g_mask = np.ma.array(g,mask=mask)

%timeit (g_mask + g_mask)**2
# 901 MS ± 52.3 MS PER LOOP ...
%timeit (g_nan + g_nan)**2
# 109 MS ± 72.2 ΜS PER LOOP ...

可以看出，Masked Array 的性能慢了接近 9 倍。

Tip

如果你不得不对含有 np.nan 的数组进行运算，那么可以尝试使用 bottleneck 库中的 nan *函数。由于并不存在 nansquare 函数，但是考虑到求方差的运算中必然包含乘方运算，因此我们可以考虑通过 nanvar 函数来评测 numpy 与 bottleneck 的性能差异。

1
2
3
4
5
6
    %timeit np.var(g_mask)
    # 587 MS ± 37.9 MS PER LOOP ...
    %timeit np.nanvar(g_nan)
    # 281 MS ± 1.46 MS PER ...
    %timeit nanvar(g_nan)
    # 61 MS ± 362 ΜS PER LOOP ...

bottleneck 要比 numpy 快接近 5 倍。如果你使用的 numpy 版本较旧，那么 bottleneck 还会快得更多。

2. ufunc

ufunc 是 Numpy 中的重要概念，它对两个输入数组同时进行逐元素的操作（比如，相加，比较大小等）。在 Numpy 中大约定义了 61 个左右的 ufunc。这些操作都是由底层的 C 语言实现的，并且支持向量化，因此，它们往往具有更快的速度。

比如，在 numpy 中，求数组中的最大值，有两个相似的函数， np.max和np.maximum可以达成这一目标。后者是 ufunc，前者不是，两者除了用法上有所区别之外，后者的速度也要快一些。

1
2
3
4
5
6
arr = np.random.normal(size=(1_000_000,))

%timeit np.max(arr)
# 801 MS ± 54.7 MS PER LOOP ...
%timeit np.maximum.reduce(arr)
# 775 MS ± 12.1 MS PER LOOP ...

np.maximum作为 ufunc，它本来是要接收两个参数的，并不能用来求一维数组的最大值。这种情况下，我们要使用reduce操作才能得到想要的结果。

这里np.maximum是一个 ufunc，则reduce是 unfunc 对象（在 Python 中，一切都是对象，包括函数）的属性之一。ufunc的其它属性还有accumulate、outer、reduceat等。

accumulate是 ufunc 中的另一个常用属性，可能你之前已经有所接触。比如，在求最大回撤时，我们就会用到它：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
# 模拟一个股价序列
n = 1000
xs = np.random.randn(n).cumsum()

# 最大回撤结束期
i = np.argmax(np.maximum.accumulate(xs) - xs) 

# 最大回撤开始期
j = np.argmax(xs[:i]) 

# 最大回撤
mdd = (xs[j] - xs[i])/xs[j]

plt.plot(xs)
plt.plot([i, j], [xs[i], xs[j]], 'o', color='Red', markersize=10)

50%

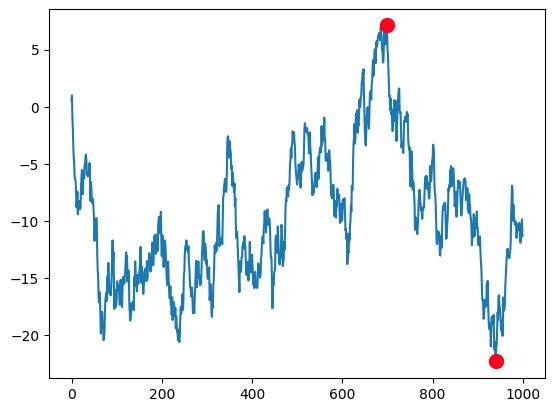
简洁就是美。在使用了accumulate之后，我们发现，计算最大回撤竟简单到只有两三行代码即可实现。

ufunc 如此好用，你可能要问，为何我用到的却不多？实际上，你很可能每天都在使用ufunc。许多二元数学操作，它们都是对 ufunc 的封装。比如，当我们调用A + B时，实际上是调用了np.add(A, B)这个 ufunc。二者在功能和性能上都是等价的。其它的 ufunc 还有逻辑运算、比较运算等。只要某种运算接受两个数组作为参数，那么，很可能 Numpy 就已经实现了相应的 ufunc 操作。此外，一些三角函数，尽管只接受一个数组参数，但它们也是 ufunc。

因此，我们需要特别关注和学习的 ufunc 函数，可能主要就是maximum，minimum等。这里再举一个在量化场景下，使用maximum的常用例子 -- 求上影线长度。

Tip

长上影线是资产向上攻击失败后留下的痕迹。它对股价后来的走势分析有一定帮助。首先，资金在这个点位发起过攻击，暴露了资金的意图。其次，攻击失败，接下来往往会有洗盘（或者溃败）。股价底部的长上影线，也被有经验的股民称为仙人指路。后面出现拉升的概率较大。上影线出现在高位时，则很可能是见顶信号。此时在较低级别的 k 线上，很可能已经出现均线拐头等比较明显的见顶信号。

现在，我们就来实现长上影线的检测。上影线的定义是：

\[ upper\_shadow = high - max(open, close) \]

下图也显示了上影线：

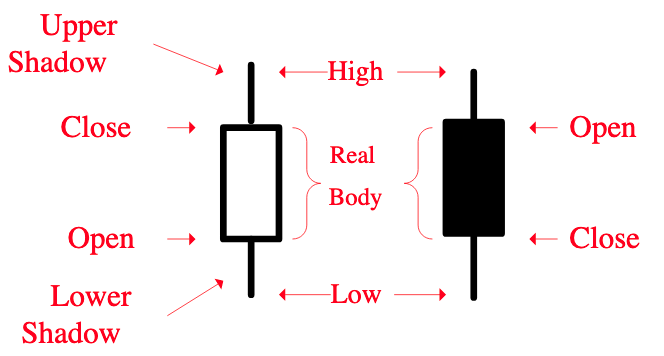
如果 upper_shadow > threshold，则可认为出现了长上影线（当然，需要对 upper_shadow 进行归一化）。检测单日的上影线很简单，我们下面的代码将演示如何向量化地求解：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
import numpy as np
import pandas as pd

rng = np.random.default_rng(seed=78)
matrix = rng.uniform(0.98, 1.02, (4, 30)).cumprod(axis=1)
opn = matrix[0]
close = matrix[-1]
high = np.max(matrix, axis=0)

upper_shadow = (high - np.maximum(opn, close))/close
np.round(upper_shadow, 2)

第 10 行的代码完全由 ufunc 组成。这里我们使用了 np.sub（减法）, np.maximum, np.divide（除法）。maximum 从两个等长的数组 opn 和 close 中，逐元素比较并取出最大的那一个，组成一个新的数组，该数组也与 opn, close 等长。

如果要求下影线长度，则可以使用 minimum。

版权声明 本课程全部文字、图片、代码、习题等所有材料，除声明引用外，均由作者本人开发。所有草稿版本均通过第三方 git 服务进行管理，作为拥有版权的证明。未经书面作者授权，请勿引用。
本文写作时，少量代码及文本参考了通义灵码生成内容。

  1. https://zh.wikipedia.org/wiki/%E9%97%B0%E7%A7%92 ↩