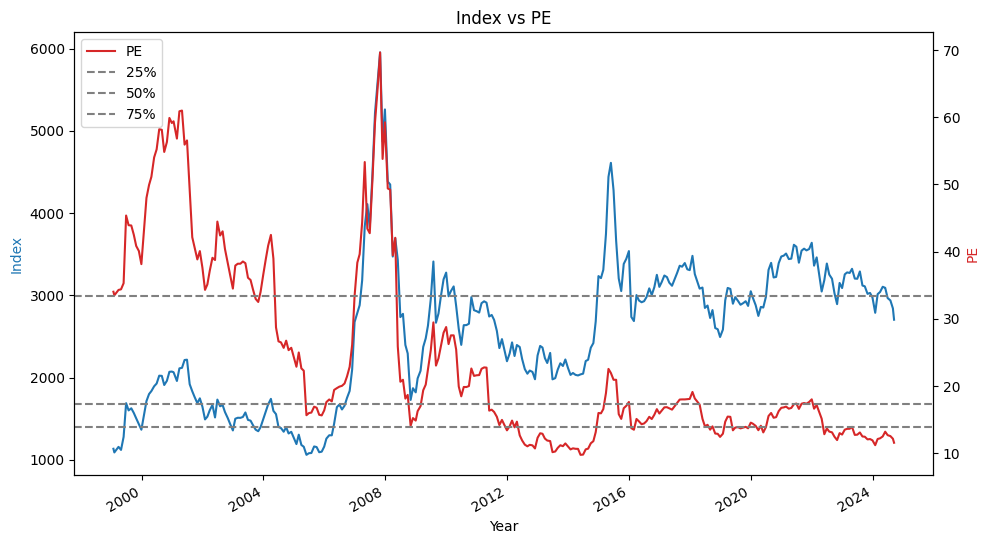
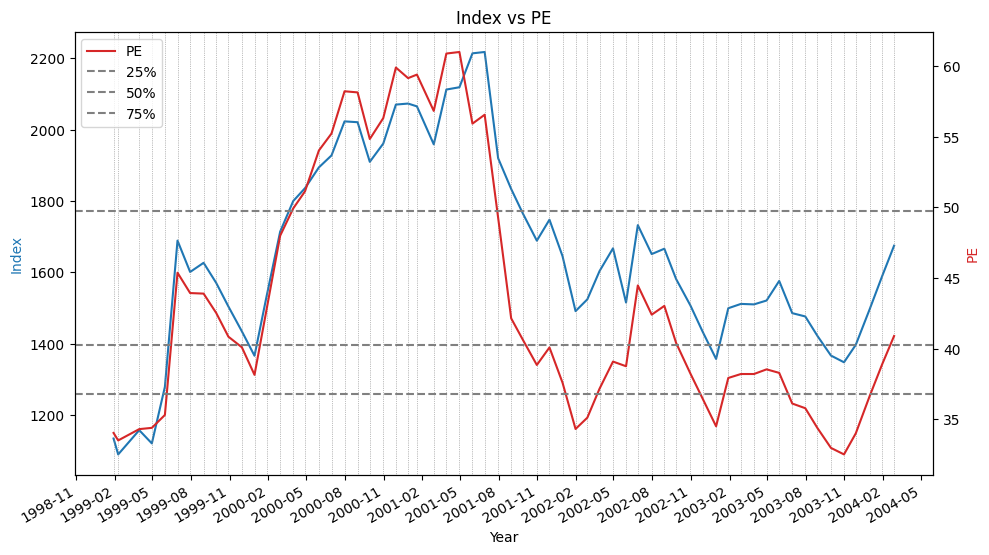
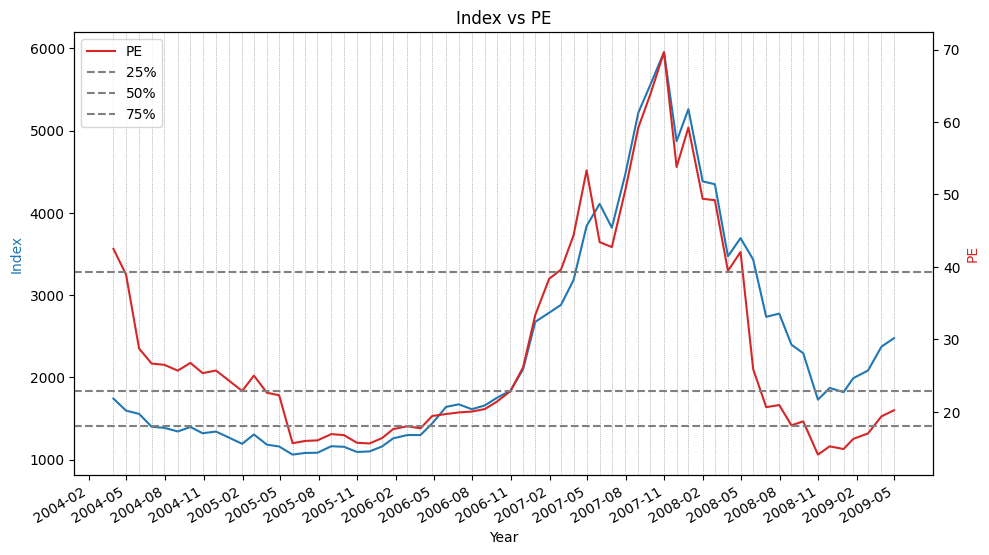
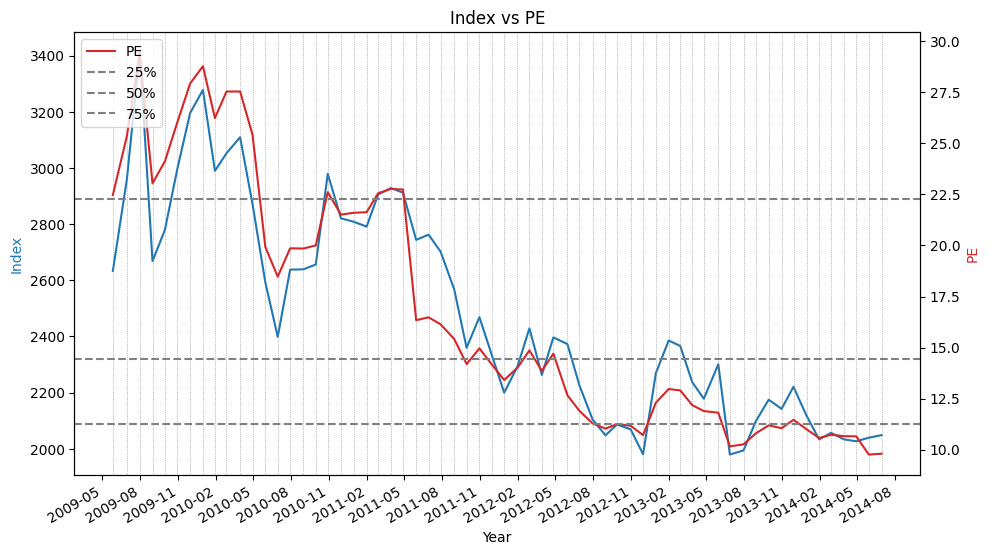
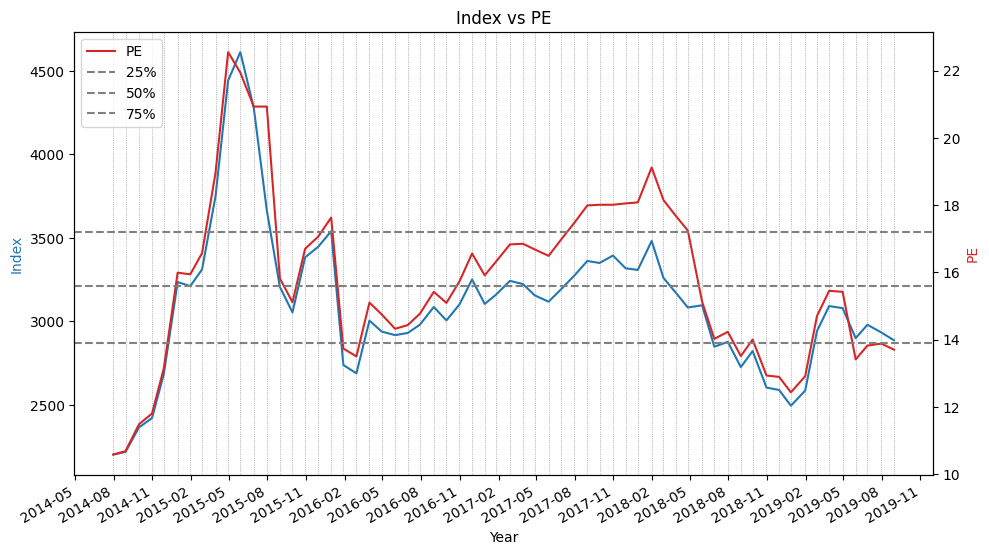
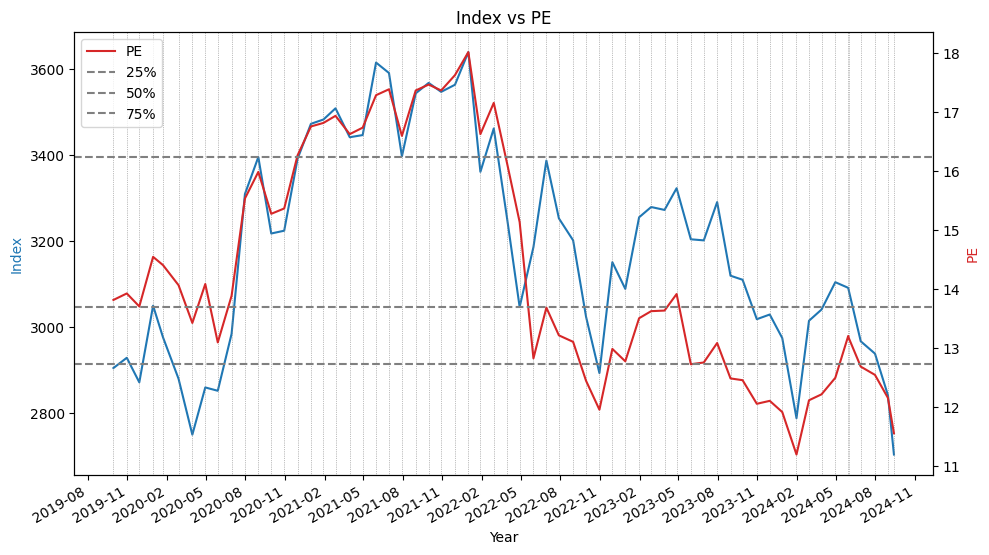
- 主要指数创今年最低周收盘,也是5年最低周收盘
- 8月有增有降,广义货币增长6.5%,狭义货币下降7.3%。
- 一意孤行!美提高部分对华301关税 中方:强烈不满 坚决反对
- 茅台业绩说明会之后,本周白酒指数再跌3.21%
- 周三(晚),美联储公布议息决议。
- 周五央行公布最新LPR利率。
- A股将有2只新股发行,创业板1只,北交所1支
- 本周大盘继续调整,主要指数均创出今年最低周收盘,也是5年最低周收盘,其中,上证指数2700点大关岌岌可危,深证成指跌破8000点大关。本周留下一个9点的跳空缺口,这是今年第一次周K线留下跳空缺口新民晚报
- 9月13日,央行发布8月社会融资规模统计数据,央行有关部门负责人进行了解读,指出央行认真贯彻落实党中央、国务院决策部署,稳健的货币政策灵活适度、精准有效,强化逆周期调节,为经济社会发展营造良好的货币金融环境。红网.财富频道
- 9月13日,美国贸易代表办公室宣布将提高部分中国商品的301关税。中方对此强烈不满,坚决反对。自9月27日起,中国制造的电动汽车的关税将上调至100%,太阳能电池上调至50%,电动汽车电池、关键矿产、钢铁、铝、口罩和岸边集装箱起重机将上调至25%,而包括半导体芯片在内的其他产品的关税上调也将在未来两年内生效。东方财富
在量化分析中,我们常常会遇到数据为 np.nan 情况。比如,某公司上年利润为负数,今年利润实现正增长,请问要如何表示公司的 YoY 的利润增长呢?
Info
np.nan 是 numpy 中的一个特殊值,表示“Not a Number”,即“不是数字”。注意,在 Numpy 中,尽管 np.nan 不是一个数字,但它确实数字类型。确切地说,它是 float 类型。此外,在 float 类型中,还存在 np.inf(正无穷大)和负无穷大 (np.NINF,或者-np.inf)。
又比如,在计算个股的 RSI 或者移动平均线时,最初的几期数据是无法计算出来的(在回测框架 backtrader 中,它把这种现象称之为技术指标的冷启动)。如果不要求返回的技术指标的取值与输入数据长度一致,则会返回短一些、但全部由有效数据组成的数组;否则,此时我们常常使用 np.NaN 或者 None 来进行填充,以确保返回的数据长度与输入数据长度一致。
但是,如果我们要对返回的数组进行统计,比如求均值、最大值、排序,对包含 np.nan 或者 None 的数组,应该如何处理?
在 numpy 中,提供了对带 np.nan 的数组进行运算的支持。比如有以下数组:
| import numpy as np
x = np.array([1, 2, 3, np.nan, 4, 5])
print(x.mean())
|
我们将得到一个 nan。实际上,多数情况下,我们希望忽略掉 nan,只对有效数据进行运算,此时得到的结果,我们往往仍然认为是有意义的。
因此,Numpy 提供了许多能处理包含 nan 数据的数组输入的运算函数。下面是一个完整的列表:
在这里,我们以输入 np.array([1, 2, 3, np.nan, np.inf, 4, 5]) 为例
| 函数 |
nan 处理 |
inf 处理 |
输出 |
| nanmin |
忽略 |
inf |
1.0 |
| nanmax |
忽略 |
inf |
inf |
| nanmean |
忽略 |
inf |
inf |
| nanmedian |
忽略 |
inf |
3.5 |
| nanstd |
传递 |
inf |
nan |
| nanvar |
传递 |
inf |
nan |
| nansum |
忽略 |
inf |
inf |
| nanquantile |
忽略 |
inf |
2.25 |
| nancumsum |
忽略 |
inf |
inf |
| nancumprod |
忽略 |
inf |
inf |
对 np.nan 的处理中,主要是三类,一类是传递,其结果导致最终结果也是 nan,比如,在计算方差和标准差时;一类是忽略,比如在找最小值时,忽略掉 np.nan,在余下的元素中进行运算;但在计算 cumsum 和 cumprod 时,"忽略"意味着在该元素的位置上,使用前值来填充。我们看一个不包含 np.inf 的示例:
| x = np.array([1, 2, 3, np.nan, 4, 5])
np.nancumprod(x)
np.nancumsum(x)
|
输出结果是:
| array([ 1., 2., 6., 6., 24., 120.])
array([ 1., 3., 6., 6., 10., 15.])
|
结果中的第 4 个元素都是由第 3 个元素复制而来的。
如果一个数组中包含 inf,则在任何涉及到排序的操作(比如 max, median, quantile)中,这些元素总是被置于数组的最右侧;如果是代数运算,则结果会被传导为 inf。这些地方,Numpy 的处理方式与我们的直觉是一致的。
除了上述函数,np.isnan 和 np.isinf 函数,也能处理包含 np.nan/np.inf 元素的数组。它们的作用是判断数组中的元素是否为 nan/inf,返回值是一个 bool 数组。
在上一节中,我们介绍的函数能够处理包含 np.nan 和 np.inf 的数组。但是,在 Python 中,None 是任何类型的一个特殊值,如果一个数组包含 None 元素,我们常常仍然会期望能对它进行 sum, mean, max 等运算。但是,Numpy 并没有专门为此准备对应的函数。
但是,我们可以通过 astype 将数组转换为 float 类型,在此过程中,所有的 None 元素都转换为 np.nan,然后就可以进行运算了。
| x = np.array([3,4,None,55])
x.astype(np.float64)
|
输出为:array([3., 4., nan, 55.])
当我们调用 np.nan *函数时,它的性能会比普通的函数慢很多。因此,如果性能是我们关注的问题,我们可以使用 bottleneck 这个库中的同名函数。
| from bottleneck import nanstd
import numpy as np
import random
x = np.random.normal(size = 1_000_000)
pos = random.sample(np.arange(1_000_000).tolist(), 5)
x[pos] = np.nan
%timeit nanstd(x)
%timeit np.nanstd(x)
|
我们担心数组中 np.nan 元素个数会影响到性能,所以,在上面的示例中,在随机生成数组时,我们只生成了 5 个元素。在随后的一次测试中,我们把 nan 元素的个数增加了 10 倍。实验证明,nan 元素的个数对性能没有什么影响。在所有的测试中,bottlenect 的性能比 Numpy 都要快一倍。
Info
根据 bottleneck 的文档,它的许多函数,要比 Numpy 中的同名函数快 10 倍左右。
随机数和采样是量化中的高频使用的操作。在造数据方面非常好用。我们在前面的示例中,已经使用过了 normal() 函数,它是来自 numpy.random 模块下的一个重要函数。借由这个函数,我们就能生成随机波动、但总体上来看又是上涨、下跌或者震荡的价格序列。
Tip
我们会在何时需要造价格序列?除了前面讲过的例子外,这里再举一例:我们想知道夏普为\(S\)的资产,它的价格走势是怎么样的?价格走势与夏普的关系如何?要回答这个问题,我们只能使用“蒙”特卡洛方法,造出若干模拟数据,然后计算其夏普并绘图。此时我们一般选造一个符合正态分布的收益率数组,然后对它进行加权(此时即可算出夏普),最后通过 np.cumprod() 函数计算出价格走势,进行绘图。
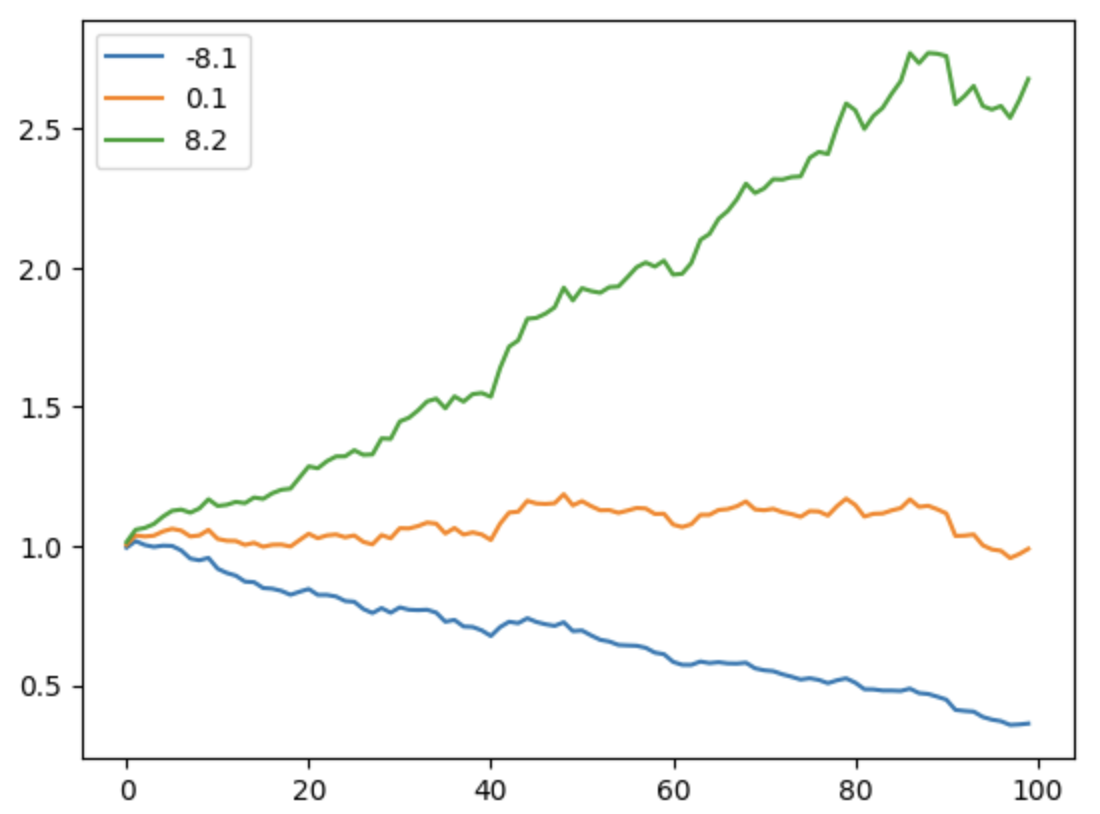
我们通过一个例子来说明夏普与股价走势之间的关系:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | import numpy as np
from empyrical import sharpe_ratio
import matplotlib.pyplot as plt
returns_ = np.random.normal(0, 0.02, size=100)
legend = []
for alpha in (-0.01, 0, 0.01):
returns = returns_ + alpha
prices = np.cumprod(returns + 1)
sharpe = sharpe_ratio(returns)
_ = plt.plot(prices)
legend.append(f"{sharpe:.1f}")
lines = plt.gca().lines
plt.legend(lines, legend)
|
从绘制的图形可以看出,当 alpha 为 1%时,夏普率可达 8.2。国内优秀的基金经理可以在一年内,做到 2~3 左右的夏普率。大家可以调整 alpha 这个参数,看看 alpha 与夏普率的关系。
迄今为止,我们在网上看到的多数关于 numpy random 的教程,都是使用的 np.random module 下面的函数。除了 normal 方法之外,random 包中还有以下函数:
| 函数 |
说明 |
| randint(a,b,shape) |
生成在区间 (a,b) 之间,形状为 shape 的随机整数数组。 |
| rand(shape) |
生成 shape 形状的随机数组,使用 [0,1) 区间的均匀分布来填充。 |
| random(shape) |
生成 shape 形状的随机数组,使用均匀分布填充 |
| randn(d1, d2, ...) |
生成 shape 形状的随机数组,使用正态分布来填充。 |
| standard_normal(shape) |
生成 shape 形状的随机数组,使用标准正态分布来填充。 |
| normal(loc,scale,shape) |
生成 shape 形状的随机数组,使用正态分布来填充,loc 是均值,scale 是标准差。 |
| choice(a,size,replace,p) |
从 a 中随机抽取 size 个元素,如果 replace=True, 则允许重复抽取,否则不允许重复抽取。p 表示概率,如果 p=None, 则表示每个元素等概率抽取。 |
| shuffle(a) |
将 a 中的元素随机打乱。 |
| seed(seed) |
设置随机数种子,如果 seed=None, 则表示使用系统时间作为随机数种子。 |
可以看出,numpy 为使用同一个功能,往往提供了多个方法。我们记忆这些方法,首先是看生成的随机数分布。最朴素的分布往往有最朴素的名字,比如,rand, randint 和 random 都用来生成均匀分布,而 normal, standard_normal 和 randn 用来生成正态分布。
除了均匀分布之外,Numpy 还提供了许多著名的分布的生成函数,比如 f 分布、gama 分布、hypergeometric(超几何分布),beta, weibull 等等。
在同一类别中,numpy 为什么还要提供多个函数呢?有一些是为了方便那些曾经使用其它知名库(比如 matlab) 的人而提供的。randn 就是这样的例子,它是 matlab 中一个生成正态随机分布的函数,现在被 numpy 移植过来了。我们这里看到的另一个函数,rand 也是这样。而对应的 random,则是 Numpy 按自己的 API 风格定义的函数。
choice 方法在量化中有比较具体的应用。比如,我们可能想要从一个大的股票池中,随机抽取 10 只股票先进行一个小的试验,然后根据结果,再考虑抽取更多的股票。
seed 函数用来设置随机数生成器的种子。在进行单元测试,或者进行演示时(这两种情况下,我们都需要始终生成相同的随机数序列)非常有用。
我们在上一节介绍了一些随机数生成函数,但没有介绍它的原理。Numpy 生成的随机数是伪随机数,它们是使用一个随机数生成器(RNG)来生成的。RNG 的输出是随机的,但是相同的输入总是会生成相同的输出。我们调用的每一个方法,实际上是在这个序列上的一个抽取动作(根据输入的 size/shape)。
在 numpy.random 模块中,存在一个全局的 RNG。在我们调用具体的随机函数时,实际上是通过这个全局的 RNG 来产生随机数的。而这个全局的 RNG,总会有人在它之上调用 seed 方法来初始化。这会产生一些问题,因为你不清楚何时、在何地、以哪个参数被人重置了 seed。
由于这个原因,现在已经不推荐直接使用 numpy.random 模块中的这些方法了。更好的方法是,为每一个具体地应用创建一个独立的 RNG,然后在这个对象上,调用相应的方法:
| rng = np.random.default_rng(seed=123)
rng.random(size=10)
|
rng 是一个 Random Generator 对象,在初始化时,我们需要给它传入一个种子。如果省略,那么 Numpy 会使用系统时间作为种子。
rng 拥有大多数前一节中提到的方法,比如 normal, f, gamma 等;但从 matlab 中移植过来的方法不再出现在这个对象上。
另外,randint 被 rng.integers 替代。
除此之外,default_rng 产生的随机数生成器对象,在算法上采用了 PCG64 算法,与之前版本采用的算法相比,它不仅能返回统计上更好的随机数,而且速度上也会快 4 倍。
Warning
在 numpy 中还存在一个 RandomState 类。它使用了较慢的梅森扭曲器生成伪随机数。现在,这个类已经过时,不再推荐使用。
我们已经介绍了 choice 的功能,现在我们来举一个例子,如何使用 choice 来平衡数据集。
在监督学习中,我们常常遇到数据不平衡的问题,比如,我们希望训练一个分类器,但是训练集的类别分布不均衡。我们可以通过 choice 方法对数据集进行 under sampling 或者 over sampling 来解决这个问题。
为了便于理解,我们先生成一个不平衡的训练数据集。这个数据集共有 3 列,其中前两列是特征(你可以想像成因子特征),第三列则是标签。
| import pandas as pd
import numpy as np
rng = np.random.default_rng(seed=42)
x = rng.random((10,3))
x[:,-1] = rng.choice([0,1], len(x), p=[0.2, 0.8])
|
我们通过下面的方法对这个数据集进行可视化,以验证它确实是一个不平衡的数据集。
| df = pd.DataFrame(x, columns=['factor1', 'factor2', 'label'])
df.label.value_counts().plot(kind='bar')
|
运行结果为:
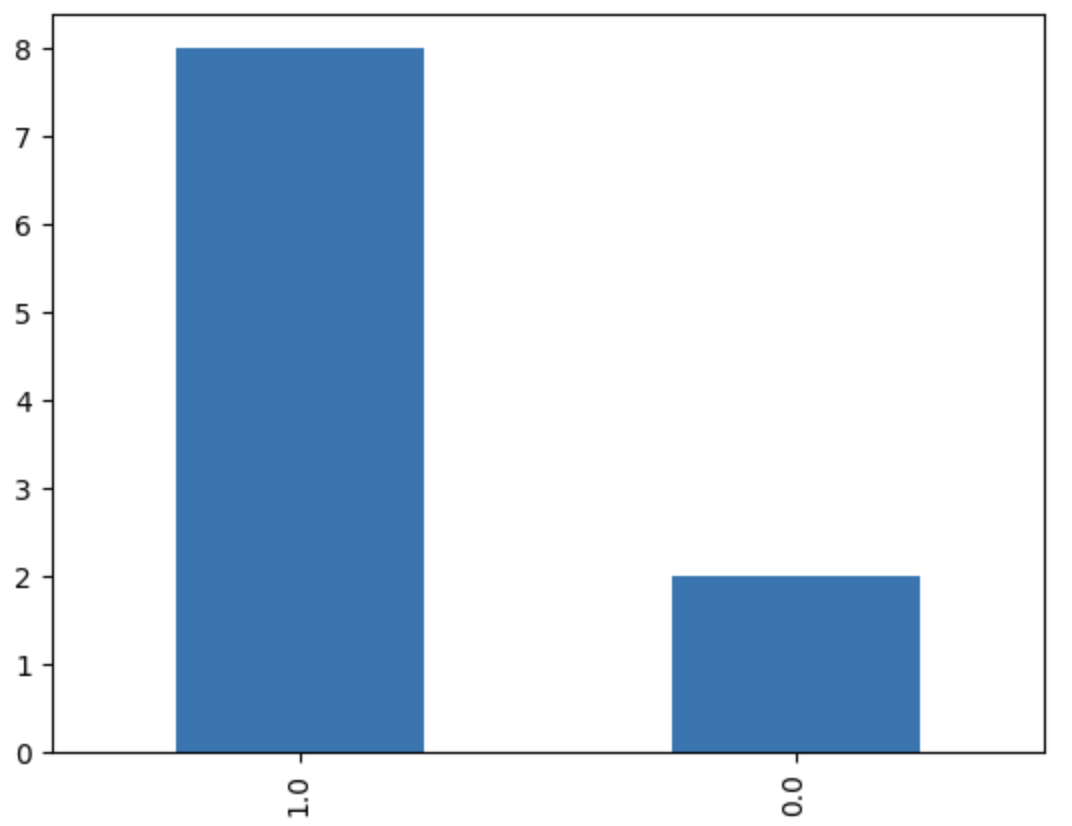
要在此基础上,得到一个新的平衡数据集,我们有两种思路,一种是 under sampling,即从多数类的数据中抽取部分数据,使得它与最小分类的数目相等;另一种是 over sampling,即从少数类的数据中复制部分数据,使得它与最大的类的数目相等。
下面的例子演示了如何进行 under sampling:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | labels, counts = np.unique(x[:,-1], return_counts=True)
# 最小分类的标签
min_label = labels[np.argmin(counts)]
# 最小分类样本的数量,作为 UNDER SAMPLING 的样本数量
min_label_count = np.min(counts)
# 最小分类无须抽取,全部提取
results = [
x[x[:,-1] == min_label]
]
# 对其它分类标签进行遍历,需要先剔除最小分类
for label in np.delete(labels, np.argmin(counts)):
sampled = rng.choice(x[x[:,-1]== label], min_label_count)
results.append(sampled)
np.concatenate(results)
|
这段代码先是找到最小分类及它的数量,然后遍历每个标签,再通过 rng.choice 对其它分类随机抽取最小分类的数量,最后把所有的子集拼接起来。
这段示例代码可用以多个标签的情况。如果要进行 over sampling,只要把其中的 min 换成 max 就可以了。
我们直接使用 Numpy 读写文件的场合并不多。提高 IO 读写性能一直都不是 Numpy 的重点,我们也只需要稍加了解即可。
Numpy 可以从 CSV 格式的文本文件中读取数据,主要有以下方法:
| api |
描述 |
| loadtxt |
解析文本格式的表格数据 |
| savetxt |
将数据保存为文本文件 |
| genfromtxt |
同上,但允许数据中有缺失值,提供了更高级的用法 |
| recfromtxt |
是 genfromtxt 的快捷方式,自动推断为 record array |
| recfromcsv |
同上,如果分隔符为逗号,无须额外指定 |
我们通过下面的示例简单演示一下各自的用法:
| import io
import numpy
buffer = io.StringIO("""1,2""")
# 默认情况下,LOADTXT 只能读取浮点数
numpy.loadtxt(buffer, delimiter=",")
|
这会输出数组array([1., 2.])。
| buffer = io.StringIO("""1,2,hello""")
# 通过指定 DTYPE 参数,可以读取其它类型
numpy.loadtxt(buffer, delimiter=",", dtype=[("age", "i4"), ("score", "f4"), ("name", "U8")])
|
这样我们将得到一个 Structured Array,其中第三列为字符串类型。如果我们不指定 dtype 参数,那么 loadtxt 将会解析失败。
| buffer = io.StringIO("""
1,2,hello
""")
numpy.genfromtxt(buffer, delimiter=",")
|
这一次我们使用了 genfromtxt 来加载数据,但没有指定 dtype 参数,genfromtxt 会将非数字列解析为 nan。因此,这段代码将输出:`array([1., 2., nan])
现在,我们也给 genfromtxt 加上 dtype 参数:
| buffer = io.StringIO("""
1,2,hello
""")
numpy.genfromtxt(buffer, delimiter=",", dtype=[("age", "i4"), ("score", "f4"), ("name", "U8")])
|
此时我们得到的结果是:array((1, 2., 'hello'), dtype=[('age', '<i4'), ('score', '<f4'), ('name', '<U8')])。注意它是 Structured Array。
recfromtxt 则不需要 dtype, 会自动推断数据类型。
| buffer = io.StringIO("""
1,2,hello
""")
numpy.recfromtxt(buffer,delimiter=",")
|
这段代码输出为rec.array((1, 2, b'hello'), dtype=[('f0', '<i8'), ('f1', '<i8'), ('f2', 'S5')])。如果推断不准确,我们也可以自己加上 dtype 参数。
如果我们使用 recfromcsv,则连 delimiter 参数都可以省掉。
| buffer = io.StringIO("""
age,score,name
1,2,hello
""")
numpy.recfromcsv(buffer)
|
输出跟上一例的结果一样。
出于速度考虑,我们还可以使用其它库来解析 CSV 文件,再转换成为 numpy 数组。比如:
| # 利用 CSV.READER() 来解析,比 NUMPY 快 8 倍
np.asarray(list(csv.reader()))
# 利用 PANDAS 来解析,比 NUMPY 快 22 倍
pd.read_csv(buffer).to_records()
|
如果我们不需要与外界交换数据,数据都是自产自销型的,也可以使用二进制文件来保存数据。
使用 numpy.save 函数来将单个数组保存数据为二进制文件,使用 numpy.load 函数来读取 numpy.save 保存的数据。这样保存的文件,文件扩展名为.npy。
如果要保存多个数组,则可以使用 savez 命令。这样保存的文件,文件扩展名为.npz。
如果有更复杂的需求,可以使用 Hdf5,pyarrow 等库来进行保存数据。
一些第三方数据源传递给我们的行情数据,常常会用字符串形式,或者整数(从 unix epoch time 起)格式来表示行情的时间。比如,akshare 和 tushare 许多接口给出的行情数据就是字符串格式;而 QMT 很多时候,会将行情时间用整数表示。掌握这些格式与 Numpy 的日期时间格式转换、以及 Numpy 到 Python 对象的时间日期转换是非常有必要的。
但是在任何编程语言中,日期和时间的处理从来都不简单。
Info
很少有程序员/研究员了解这一点:日期和时间并不是一个数学上或者物理上的一个客观概念。时区的划分、夏令时本身就是一个政治和法律上的概念;一些地方曾经使用过夏令时,后来又取消了这种做法。其次,关于闰秒 的决定,也并不是有章可循的,它是由一个委员会开会来临时决定的。这种决定每年做一次。
所有这些决定了我们无法通过一个简单的数学公式来计算时间及其变化,特别是在时区之间的转换。
关于时间,首先我们要了解有所谓的 timezone aware 时间和 timezone naive 时间。当我们说到晚上 8 时开会时,这个时间实际上默认地包含了时区的概念。如果这是一个跨国会议,但你在通知时不告诉与会方时区,就会导致其它人无法准时出席 -- 他们将会在自己时区的晚上 8 时上线。
如果一个时间对象不包含时区,它就是 timezone naive 的;否则,它是 timezone aware 的。但这只是针对时间对象(比如,Python 中的 datetime.datetime)才有的意义;日期对象(比如,Python 中的 datetime.date)是没有时区的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | import pytz
import datetime
# 通过 DATETIME.NOW() 获得的时间没有时区信息
# 返回的是标准时间,即 UTC 时间,等同于调用 UTCNOW()
now = datetime.datetime.now()
print(f"now() without param: {now}, 时区信息{now.tzinfo}")
now = datetime.datetime.utcnow()
print(f"utcnow: {now}, 时区信息{now.tzinfo}")
# 构造 TIMEZONE 对象
cn_tz = pytz.timezone('Asia/Shanghai')
now = datetime.datetime.now(cn_tz)
print(f"现在时间{now}, 时区信息{now.tzinfo}")
|
| print("现在日期:", now.date())
try:
print(now.date().tzinfo)
except AttributeError:
print("日期对象没有时区信息")
|
上述代码将依次输出:
| now() 不带参数:2024-05-19 11:03:41.550328, 时区信息 None
utcnow: 2024-05-19 11:03:41.550595, 时区信息 None
现在时间 2024-05-19 19:03:41.550865+08:00, 时区信息 Asia/Shanghai
现在日期:2024-05-19
日期对象没有时区信息
|
不过,限于篇幅,我们对时间问题的介绍只能浅尝辄止。在这里,我们主要关注在 Numpy 中,日期/时间如何表示,它们彼此之间如何比较、转换,以及如何与 Python 对象进行比较和转换。
在 Numpy 中,日期/时间总是用一个 64 位整数(np.datetime64)来表示,此外,还关联了一个表示其单位(比如,纳秒、秒等)的元数据结构。np.datetime64是没有时区概念的。
| tm = np.datetime64('1970-01-01T00:00:00')
print(tm)
print(tm.dtype)
|
这将显示为:
| 1970-01-01T00:00:00
datetime64[s]
|
这里的[s]就是我们前面所说的时间单位。其它常见单位还有[ms]、[us]、[ns]等等。
除了从字符串解释之外,我们还可以直接将 Python 对象转换成np.datetime64,反之亦然:
| tm = np.datetimet64(datetime.datetime.now())
print(tm)
print(tm.item())
print(tm.astype(datetime.datetime))
|
下面我们来看看如何实现不同格式之间的批量转换。这在处理 akshare, tushare 或者 QMT 等第三方数据源提供的行情数据时,非常常见。
首先我们构造一个时间数组。顺便提一句,这里我们将使用np.timedelta64这个时间差分类型:
| now = np.datetime64(datetime.datetime.now())
arr = np.array([now + np.timedelta64(i, 'm') for i in range(3)])
arr
|
输出结果如下:
| array(['2024-05-19T12:57:47.349178',
'2024-05-19T12:58:47.349178',
'2024-05-19T12:59:47.349178'],
dtype='datetime64[us]')
|
我们可以通过np.datetime64.astype()方法将时间数组转换为 Python 的时间对象:
| time_arr = arr.astype(datetime.datetime)
# 转换后的数组,每个元素都是 TIMEZONE NAIVE 的 DATETIME 对象
print(type(time_arr[0]))
# !!! 技巧
# 如何把 NP.DATETIME64 数组转换为 PYTHON DATETIME.DATE 数组?
date_arr = arr.astype('datetime64[D]').astype(datetime.date)
# 或者 -- 两者的容器不一样
date_arr = arr.astype('datetime64[D]').tolist()
print(type(date_arr[0]))
|
这里的关键是,我们之前生成的arr数组,其元素类型为np.datetime64[us]。它到 Python datetime.date的转换将损失精度,所以 Numpy 要求我们显式地指定转换类型。
如何将以字符串表示的时间数组转换为 Numpy datetime64 对象数组呢?答案仍然是 astype() 方法。
| # 将时间数组转换为字符串数组
str_arr_time = arr_time.astype(str)
print(str_arr_time)
# 再将字符串数组转换为 DATETIME64 数组,精度指定为 D
str_arr_time.astype('datetime64[D]')
|
显示结果为:
| array(['2024-05-19T12:57:47.349178',
'2024-05-19T12:58:47.349178',
'2024-05-19T12:59:47.349178'],
dtype='datetime64[us]')
array([
'2024-05-19',
'2024-05-19'],
dtype='datetime64[D]')
|
最后,我们给一个 QMT 获取交易日历后的格式转换示例。在 QMT 中,我们通过get_trading_dates来获取交易日历,该函数返回的是一个整数数组,每个元素的数值,是从 unix epoch 以来的毫秒数。
我们可以通过以下方法对其进行转换:
| import numpy as np
days = get_trading_dates('SH', start_time='', end_time='', count=10)
np.array(days, dtype='datetime64[ms]').astype(datetime.date)
|
QMT 官方没有直接给出交易日历转换方案,但给出了如何将 unix epoch 时间戳转换为 Python 时间对象(但仍以字符串表示):
1
2
3
4
5
6
7
8
9
10
11
12 | import time
def conv_time(ct):
'''
conv_time(1476374400000) --> '20161014000000.000'
'''
local_time = time.localtime(ct / 1000)
data_head = time.strftime('%Y%m%d%H%M%S', local_time)
data_secs = (ct - int(ct)) * 1000
time_stamp = '%s.%03d' % (data_head, data_secs)
return time_stamp
conv_time(1693152000000)
|
我们需要对每一个数组元素使用上述解析方法。官方方案的优点是不依赖任何三方库。不过,没有量化程序能离开 Numpy 库,所以,我们的方案并未增加第三方库的依赖。
你的数据源、或者本地存储方案很可能使用 Numpy Structured Array 或者 Rec Array 返回证券列表。很显然,证券列表中一定会包括字符串,因为它一定会存在证券代码列和证券名称列。有一些还会返回证券的地域属性和其它属性,这也往往是字符串。
对证券列表,我们常常有以下查询操作:
- 获取在某个板块上市的股票列表,比如,北交所、科创板和创业板与主板的个股交易规则上有一些不同,因此,我们的策略很可能需要单独为这些板块构建。这就有了按板块过滤证券列表的需要。也可能我们要排除 ST,刚上市新股。这些都可以通过字符串操作来实现。
- 市场上有时候会出现魔幻的名字炒作。比如龙年炒龙字头(或者含龙的个股)、炒作“东方”、炒作“中”字头。作为量化人,参与这样的炒作固然不可取,但我们要拥有分析市场、看懂市场的能力。
Numpy 中的大多数字符串操作都封装在 numpy.char 这个包下面。它主要提供了一些用于格式化的操作(比如左右填充对齐、大小写转换等)、查找和替换操作。
下面的代码展示了如何从证券列表中过滤创业板:
1
2
3
4
5
6
7
8
9
10
11
12 | import numpy as np
import numpy.char as nc
# 生成 STRUCTURED ARRAY, 字段有 SYMBOL, NAME, IPO DATE
arr = np.array([('600000.SH', '中国平安', '1997-08-19'),
('000001.SZ', '平安银行', '1997-08-19'),
('301301.SZ', '川宁生物', '2012-01-01')
], dtype=[('symbol', 'S10'), ('name', 'S10'), ('ipo_date', 'datetime64[D]')])
def get_cyb(arr):
mask = np.char.startswith(arr["symbol"], b"30")
return arr[mask]
|
Question
我们在查找创业板股票时,使用的是 b"30"来进行匹配。为何要用 b"30"而不是"30"?
注意第 11 行,我们要通过np.char.startswith()来使用startswith函数。任何一个 numpy array 对象都没有这个方法。
".SZ"是我们的数据源给股票编制的交易所代码。不同的数据源,可能使用不同的交易所代码。比如,聚宽数据源会使用.XSHG 表示上交所,.XSHE 表示深交所。现在,如果我们要将上述代码转换为聚宽的格式,应该如何操作?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | # 生成 STRUCTURED ARRAY, 字段有 SYMBOL, NAME, IPO DATE
arr = np.array([('600000.SH', '中国平安', '1997-08-19'),
('000001.SZ', '平安银行', '1997-08-19'),
('301301.SZ', '川宁生物', '2012-01-01')
], dtype=[('symbol', 'U10'), ('name', 'U10'), ('ipo_date', 'datetime64[D]')])
def translate_exchange_code(arr):
symbols = np.char.replace(arr["symbol"], ".SH", ".XSHG")
print(symbols)
symbols = np.char.replace(symbols, ".SZ", ".XSHE")
arr["symbol"] = symbols
return arr
translate_exchange_code(arr)
|
这一次,我们把 symbol 和 name 的定义改为 Unicode 型,以避免我们查找时,要输入像 b"30"这样的字面量。
但输出的结果可能让人意外,因为我们将得到这样的输出:
| array([('600000.XSH', '中国平安', '1997-08-19'),
('000001.XSH', '平安银行', '1997-08-19'),
('301301.XSH', '川宁生物', '2012-01-01')],
dtype=[('symbol', '<U10'), ('name', '<U10'), ('ipo_date', '<M8[D]')])
|
Question
发生了什么?我们得到了一堆以".XSH"结尾的 symbol,它们本应该是"600000.XSHG"这样的字符串。错在哪里,又该如何修改?
在上面的示例中,如果我们把替换字符串改为空字符串,就实现了删除操作。这里就不演示了。
char 模块还提供了字符串相等比较函数equal:
| arr = array([('301301.SZ', '川宁生物', '2012-01-01')],
dtype=[('symbol', '<U10'), ('name', '<U10'), ('ipo_date', '<M8[D]')])
arr[np.char.equal(arr["symbol"], "301301.SZ")]
|
在这个特殊的场景下,我们也可以直接使用以下语法:
| arr[arr["symbol"] == "301301.SZ"]
|
Tip
np.char 下的函数很多,如何记忆?实际上,这些函数多数是 Python 中 str 的方法。如果你熟悉 Pandas,就会发现 Pandas 中也有同样的用法。因此,像upper, lower, strip这样的str函数,你可以直接拿过来用。
Numpy 中的字符串函数另一个比较常用的场景,就是执行格式化。你可以通过ljust, 'center', rjust在显示一个数组前,将它们的各列数据进行左右空格填充,这样,输出时就可以比较整齐。
Question
2024 年 5 月 10 日起,南京化纤走出 7 连板行情,短短 7 日,股价翻倍。市场上还有哪些名字中包含化纤的个股?它们的涨跌是否存在相关性或者跨周期相关性?
你可能常常在一些接近底层的库中,看到 Numpy masked array 的用法。Masked Array 是 Numpy 中很重要的概念。考虑这样的情景,你有一个数据集,其中包含了一些缺失的数据或者无效值。这些”不合格“的数据,可能以 np.nan,np.inf, None 或者其它仅仅是语法上有效的值来表示(比如,在 COVID-19 数据集中,病例数出现负数)的。
如何在保持数据集的完整性不变的前提下,仍然能对数据进行运算呢?
Note
这里有一个真实的例子。你可以在 Kaggle 上找到一个 COVID-19 的数据集,这个数据集中,就包含了累积病例数为负数的情况。该数据集由 Johns Hoopkins University 收集并提供。
很显然,我们无法直接对这些数据进行运算。请看下面的例子:
| x = np.array([1, 2, 3, np.inf, np.nan, None])
np.mean(x)
np.nanmean(x)
|
只要数据中包含 np.nan, np.inf 或者 None,numpy 的函数就无法处理它们。即使数据在语法上合法,但在语义上无效,Numpy 强行进行计算,结果也是错误的。
这里有一个量化中可能遇到的真实场景,某公司有一年的年利润为零,这样使得它的 YoY 利润增长在次年变得无法计算。如果我们需要利用 YoY 数据进一步进行运算,我们就需要屏蔽这一年的无效值。否则,我们会连 YoY 利润的均值都无法计算出来。
这里有一个补救的方法,就是将原数据拷贝一份,并且将无效值替换为 np.nan。此后多数运算,都可以用np.nan*来计算。这个方法我们已经介绍过了。但是,如果你是原始数据的收集者,显然你应该照原样发布数据,任何修改都是不合适的;如果你是数据的应用者,当然应该对数据进行预处理后,才开始运算。但是,你又很可能缺少了对数据进行预处理所必须的信息 -- 你怎么能想到像-1, 0 这样看起来人畜无害的小可爱们,竟然是隐藏着的错误呢?
为了解决这个问题,Numpy 就提供了 Masked Array。但是我们不打算在 Masked Array 上过多着墨。关于 Masked Array,我们可以借用这样一句话,很多人不需要知道 Masked Array,知道 Masked Array 的人则已经精通它了。
有一点需要注意的是,仅在需要时,使用 Masked Array。因为可能与您相像的相反,Masked Array 不会提高性能,反而,它大大降低了性能:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | import numpy as np
# NUMPY VERSION 1.24.4
g = np.random.random((5000,5000))
indx = np.random.randint(0,4999,(500,2))
g_nan = g.copy()
g_nan[indx] = np.nan
mask = np.full((5000,5000),False,dtype=bool)
mask[indx] = True
g_mask = np.ma.array(g,mask=mask)
%timeit (g_mask + g_mask)**2
# 901 MS ± 52.3 MS PER LOOP ...
%timeit (g_nan + g_nan)**2
# 109 MS ± 72.2 ΜS PER LOOP ...
|
可以看出,Masked Array 的性能慢了接近 9 倍。
Tip
如果你不得不对含有 np.nan 的数组进行运算,那么可以尝试使用 bottleneck 库中的 nan *函数。由于并不存在 nansquare 函数,但是考虑到求方差的运算中必然包含乘方运算,因此我们可以考虑通过 nanvar 函数来评测 numpy 与 bottleneck 的性能差异。
| %timeit np.var(g_mask)
# 587 MS ± 37.9 MS PER LOOP ...
%timeit np.nanvar(g_nan)
# 281 MS ± 1.46 MS PER ...
%timeit nanvar(g_nan)
# 61 MS ± 362 ΜS PER LOOP ...
|
| bottleneck 要比 numpy 快接近 5 倍。如果你使用的 numpy 版本较旧,那么 bottleneck 还会快得更多。
|
ufunc 是 Numpy 中的重要概念,它对两个输入数组同时进行逐元素的操作(比如,相加,比较大小等)。在 Numpy 中大约定义了 61 个左右的 ufunc。这些操作都是由底层的 C 语言实现的,并且支持向量化,因此,它们往往具有更快的速度。
比如,在 numpy 中,求数组中的最大值,有两个相似的函数, np.max和np.maximum可以达成这一目标。后者是 ufunc,前者不是,两者除了用法上有所区别之外,后者的速度也要快一些。
| arr = np.random.normal(size=(1_000_000,))
%timeit np.max(arr)
# 801 MS ± 54.7 MS PER LOOP ...
%timeit np.maximum.reduce(arr)
# 775 MS ± 12.1 MS PER LOOP ...
|
np.maximum作为 ufunc,它本来是要接收两个参数的,并不能用来求一维数组的最大值。这种情况下,我们要使用reduce操作才能得到想要的结果。
这里np.maximum是一个 ufunc,则reduce是 unfunc 对象(在 Python 中,一切都是对象,包括函数)的属性之一。ufunc的其它属性还有accumulate、outer、reduceat等。
accumulate是 ufunc 中的另一个常用属性,可能你之前已经有所接触。比如,在求最大回撤时,我们就会用到它:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | # 模拟一个股价序列
n = 1000
xs = np.random.randn(n).cumsum()
# 最大回撤结束期
i = np.argmax(np.maximum.accumulate(xs) - xs)
# 最大回撤开始期
j = np.argmax(xs[:i])
# 最大回撤
mdd = (xs[j] - xs[i])/xs[j]
plt.plot(xs)
plt.plot([i, j], [xs[i], xs[j]], 'o', color='Red', markersize=10)
|
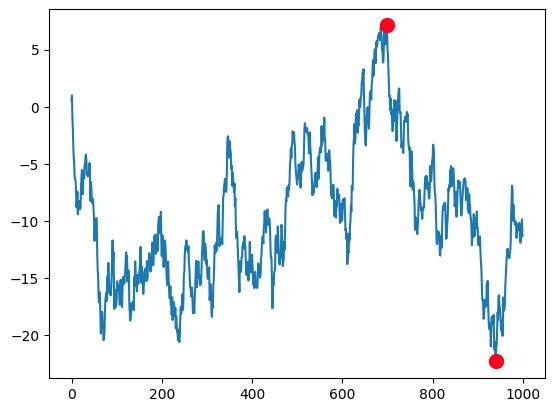
简洁就是美。在使用了accumulate之后,我们发现,计算最大回撤竟简单到只有两三行代码即可实现。
ufunc 如此好用,你可能要问,为何我用到的却不多?实际上,你很可能每天都在使用ufunc。许多二元数学操作,它们都是对 ufunc 的封装。
比如,当我们调用A + B时,实际上是调用了np.add(A, B)这个 ufunc。二者在功能和性能上都是等价的。其它的 ufunc 还有逻辑运算、比较运算等。只要某种运算接受两个数组作为参数,那么,很可能 Numpy 就已经实现了相应的 ufunc 操作。此外,一些三角函数,尽管只接受一个数组参数,但它们也是 ufunc。
因此,我们需要特别关注和学习的 ufunc 函数,可能主要就是maximum,minimum等。这里再举一个在量化场景下,使用maximum的常用例子 -- 求上影线长度。
Tip
长上影线是资产向上攻击失败后留下的痕迹。它对股价后来的走势分析有一定帮助。首先,资金在这个点位发起过攻击,暴露了资金的意图。其次,攻击失败,接下来往往会有洗盘(或者溃败)。股价底部的长上影线,也被有经验的股民称为仙人指路。后面出现拉升的概率较大。上影线出现在高位时,则很可能是见顶信号。此时在较低级别的 k 线上,很可能已经出现均线拐头等比较明显的见顶信号。
现在,我们就来实现长上影线的检测。上影线的定义是:
\[
upper\_shadow = high - max(open, close)
\]
下图显示了上影线:
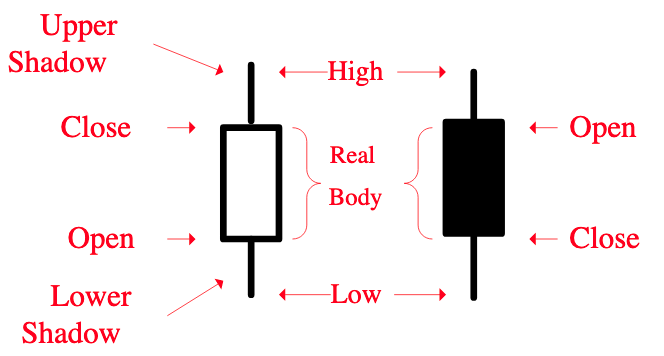
如果 \(\(upper\_shadow > threshold\)\),则可认为出现了长上影线(当然,需要对 upper_shadow 进行归一化)。检测单日的上影线很简单,我们下面的代码将演示如何向量化地求解:
| import numpy as np
import pandas as pd
rng = np.random.default_rng(seed=78)
matrix = rng.uniform(0.98, 1.02, (4, 30)).cumprod(axis=1)
opn = matrix[0]
close = matrix[-1]
high = np.max(matrix, axis=0)
upper_shadow = (high - np.maximum(opn, close))/close
np.round(upper_shadow, 2)
|
第 10 行的代码完全由 ufunc 组成。这里我们使用了 np.sub(减法), np.maximum, np.divide(除法)。maximum 从两个等长的数组 opn 和 close 中,逐元素比较并取出最大的那一个,组成一个新的数组,该数组也与 opn, close 等长。
如果要求下影线长度,则可以使用 minimum。