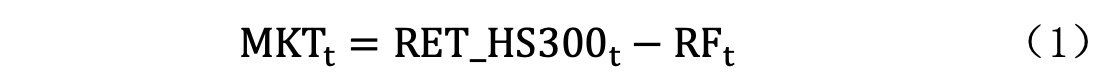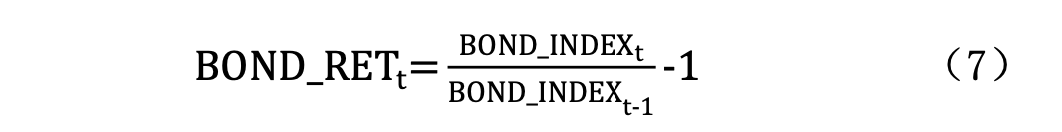跳转至


课程  因子投资  机器学习  story  量化传奇  Python  Poetry  ppw  算法  hdbscan  聚类  选股  Algo  minimum  numpy  algo  FFT  模式识别  配对交易  GBDT  LightGBM  XGBoost  statistics  CDF  KS-Test  回测  过拟合  algorithms  machine learning  strategy  python  sklearn  Info  interview  career  xgboost  PCA  wavelet  Figures  Behavioral Economics  人物  职场  Quantopian  figure  Banz  rsi  zigzag  穹顶压力  因子  pe  ORB  策略  Xgboost  factor  alpha101  alpha  技术指标  wave  quant  algorithm  pearson  spearman  因子分析  Alphalens  涨停板  herd-behaviour  因子策略  momentum  因子评估  review  trade  history  indicators  zscore  波动率  顶背离  freshman  resources  others  AI  DeepSeek  network  tools  weekly  pandas  quantlib  jupyter-notebook  pypinyin  qmt  xtquant  blog  static-site  duckdb  工具  colors  free resources  barra  world quant  Alpha  pdf  openbb  数据  arsenal  copilot  vscode  code  量化数据存储  hdf5  h5py  Jupyter  jupysql  pyarrow  parquet  数据源  实盘  clickhouse  programming  notebook  Numpy  Pandas 


Index

  • 需要 2 分钟阅读时间

7因子模型，除了规模、市场、动量和价值，还有哪些？

这篇文章的源起是有读者问，七因子模型除了规模、市场、动量和价值之外，还包括哪几个因子？就这个题目，正好介绍一下Fung & Hsieh的七因子模型。

七因子模型一般是指David Hsieh和William Fung于2004年在一篇题为《Hedge Fund Benchmarks: A Risk Based Approach》中提出的7 factor model。

L50 作者David Hsieh 出生于香港，是Duke大学教授，在对冲基金和另类beta上有着深入而广泛的研究。William Fung则是伦敦商学院对冲基金教育研究中心的客座教授。

这篇论文发表以来，共获得了1300多次引用。作者也以此论文获得了由CFA颁发的格雷厄姆和多德杰出贡献奖及费雪.布莱克纪念基金会奖等几个奖励。因此，这篇论文在量化史上还是有一定地位的，值得我们学习。

在这篇论文中，7因子模型指的是以下7个：

  1. Bond Trend-Following Factor 债券趋势跟随因子
  2. Currency Trend-Following Factor 货币趋势跟随因子
  3. Commodity Trend-Following Factor 商品趋势跟踪因子
  4. Equity Market Factor 股票市场因子
  5. The Equity Size Spread Factor 股票规模利差因子
  6. The Bond Market Factor 债券市场因子
  7. The Bond Size Spread Factor 债券规模利差因子

这几个因子中，股票市场因子、规模利差因子本质上就是市场因子和规模因子。

前三个因子来自Fung和Hsieh另一篇论文：《The Risk in Hedge Fund Strategies: Theory and Evidence from Trend Followers》。 这篇论文发表几年后， Fung和Hsieh又增加了第8个因子，即MSCI新兴市场指数。

这篇论文中还介绍了对冲基金研究中几个常见的偏差（bias），这里也重点介绍下。

Tip

在投资中了解什么是错的、怎么错的，可能比了解什么是对的更重要，毕竟，投资中，只有正确的方法和方法论是持久发作用的，而所谓“正确的结论”，都只是一时一地的产物。

研究对冲基金时，第一个容易出现的偏差是选择偏差。共同基金（即公募基金）需要公开批露他们的投资活动，但对冲基金则不需要。对冲基金的数据一般由数据供应商收集，在这种收集过程中，就可能出现选择偏差，从而使得数据库中的基金样本不是整个基金样本的代表性样本。

第二是幸存者偏差。这是所有基金研究中的一个常见问题。我们在课程中讲过，股票的上市和退市都比较严格，公司即使退市，它的历史数据也能很容易获取到；但已停止运营的基金则会从数据库中剔除掉。这一点除了本文有提到，在其它许多论文中也有提到。

第三个偏差是即时历史偏差(instant history bias)。当基金进入数据库时，它会把过去的业绩历史记录也带入进来，尽管这些业绩记录是在孵化期创建的。并且，如果一支基金在孵化期的业绩不够好，他们也往往会停止运营。显然，这样的业绩记录并不完全真实可靠。

在量化研究中如何避免各种系统偏差是很重要的经验和技巧。这些经验并不来自于学术研究，掌握这些经验需要我们了解数据加工处理的过程 -- 很多人无法直接了解到数据收集到加工的全过程，因此行业交流是十分重要的。

回到正题。读者的提问是，在七因子模型中，除了市场、规模、价值和动量，其它几个因子是什么。这个问题可能来源于国内私募在用的一个8因子模型。

这个模型由清华大学国家金融研究院在2017年3月的一个简报（中国私募基金8因子模型）中作出批露。它参考了Fung和Hsieh的7因子模型，提出了8个因子，分别是：

  1. 股票市场风险因子（MKT）
  2. 规模因子（SMB）
  3. 价值因子（HML)
  4. 动量因子（MOM）
  5. 债券因子（BOND10)
  6. 信用风险因子（CBMB10)
  7. 债券市场综合因子（BOND_RET）
  8. 商品市场风险因子

不难看出，这个8因子模型是在经典的FF三因子（规模、市场、价值）基础上，增加了动量因子（Titman和Jegadesh），再结合Fung和Hsieh的七因子中的一些因子构成的。

在这个模型中，股票市场风险因子定义为：

\(RET_HS300_t\)为第\(t\)月的沪深300指数的月收益率， \(RF_t\)为第\(t\)月1年期定期存款利率的月利率。这点比较意外，一般来说，国债的风险比存款还要低（大额存款有50万的止付额），但收益要高一些，一般多会使用国债利率作为无风险收益率。

它的规模因子构建方法是，以一年为期进行一次换手。在每年6月底构建一次投资组合，将A股按流通市值将样本股票等分为小盘组和大盘组，再根据T-1期年报中的账面市值比和A股流通市值（ME）计算出账面市值比后，将股票按30%, 40%, 30%的比例划分为成长组、平衡组和价值组。最后，将两种分组方式所得的结果，按笛卡尔积的方式组成为六组，再计算各组的月收益率。

它的价值因子、动量因子构建方法与规模因子类似。

债券因子公式为：

75%

信用风险因子为：

75%

债券市场综合因子公式为：

75%

数据使用的是中债综合全价指数。文章虽然只有10页的篇幅，但在因子构建方面讲解得比较详细，感兴趣的同学可以找来一读。

题图是杜克大学的地标 - Duke Chapel（杜克教堂）。我曾经开车路过杜克大学，当时心想，哈，这就是杜克大学了，可惜事前没有安排，没能进去参观。

从CAPM、APT以来，各种因子被源源不断地提出，形成了所谓的因子动物园一说。这么多因子，如何进行学习？如何梳理它们的脉络？对初学者而言，可能会一时没有头绪。我们准备了一个系统的量化课程（《量化二十四课》），并且即将开设新的因子分析及机器学习策略课程，欢迎咨询。现在报名《量化二十四课》，还可以免费升级到《因子分析及机器学习策略》课程。

文中提及的两篇论文，可以在这里找到链接下载。

  • 需要 2 分钟阅读时间

4k stars! 如何实现按拼音首字母查询证券代码？

一个可能只有少数量化人才需要的功能 -- 按拼音首字母来查找证券。比如，当我们键入ZGPA时，就能搜索出中国平安，或者是它的代码。这是我们使用行情软件时常用的一个功能。

这个功能的关键是要实现汉字转拼音。有的数据源已经提供了这个查询。但不是所有的数据源都有这个功能。

如果我们使用的数据源是聚宽(jqdatasdk)，当我们调用jq.get_all_securities时，它返回的证券列表，将包括以下几项：

  • index，证券代码代码，比如000001.XSHE
  • display_name，证券的中文名，比如平安银行
  • name，证券的拼音首字母名，比如PAYH
  • start_date，证券IPO日
  • end_date，该品种退市日。只有在已退市时，此时间才有效。
  • type，证券类型，取值可能是stock, index, fund等。

我们要的关系反映在字段name与index, display_name中。当用户输入PAYH时，通过查找上述表格，就能找到对应的中文名，或者它的代码。

但如果我们使用的数据源（比如QMT）没有提供这个信息呢？这时我们就需要通过第三方库来将汉字转换成为拼音。

这里的难点在于多音字，比如，平安银行应该转换成PAYH，而不是PAYX。我们考察了好几个python第三方库，比如pinyin, xpinyin，最后发现只有pypinyin能较好地实现这个功能。

功能介绍

pypinyin库在github上获得了4.6k stars。与之相对照，xpinyin有800多个stars，pinyin是超过200个stars。

你可能会好奇，这个功能主要是什么人在用，为什么能拿到这么多star。这么多star，可能主要是做AI的人给的。

将汉字转换成拼音再进行深度学习，是内容审查的一个研究方向。

pypinyin成功的原因主要是在多数情况下，能给出正确的拼音。如果遇到无法正确处理的词，我们还可以通过自定义词组拼音库来进行修正。其次，它提供了简单的繁体支持、多种注意风格支持等。

安装和使用

我们通过下面的命令来安装：

1
pip install pypinyin

它主要提供了两个API，即pinyin和lazy_pinyin。但在使用时，我们还需要指定风格(Style)。下面我们看几个简单的例子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
>>> from pypinyin import pinyin, lazy_pinyin, Style
>>> pinyin('中心')
[['zhōng'], ['xīn']]

# 启用多音字模式
>>> pinyin('中心', heteronym=True) 
[['zhōng', 'zhòng'], ['xīn']]

# lazy_pinyin
>>> lazy_pinyin('中国平安') 
['zhong', 'guo', 'ping', 'an']

lazy_pinyin这个API的特点是（与pinyin相比），它的返回值中，每一个字都只包含一个读音，因此，对每一个字，它返回的是一个字符串，而不是一个数组。

我们来看看它会不会把中国银行拼成zhong guo yin xing:

1
2
>>> lazy_pinyin('中国银行') 
['zhong', 'guo', 'yin', 'hang']

这个结果是正确的。再回到我们最初的问题，如何得到拼音首字母呢？这就需要我们传入style参数了：

1
2
3
4
5
6
7
>>> lazy_pinyin('中国银行', style=Style.FIRST_LETTER) 
['z', 'g', 'y', 'h']

# 将其转换成为大写
>>> py = lazy_pinyin('中国银行', style=Style.FIRST_LETTER)
>>> "".join(py).upper()
'ZGYH'
这里我们传入的参数是Style.FIRST_LETTER。还有一个与此相混淆的参数，style.INITIALS。如果我们传入此参数：

1
2
>>> lazy_pinyin('中国银行', style=Style.INITIALS)
['zh', 'g', '', 'h']

结果可能令人意外。要理解它的输出，需要一些拼音的知识。我们只要记住，要得到拼音首字母，应该传入Style.FIRST_LETTER参数。

令人吃惊的是，通过pypinyin给出的首字母结果，竟然比聚宽给出的结果要正确。

比如，像重药控股，该公司处在重庆，因此第一个字应该发音chong。聚宽数据给出的拼音是ZYKG，而不是CYKG。又比如长源电力，该公司地处湖北，“长”字可能来源于长江，因此一般读出Chang Yuan Dian Li，聚宽的数据给出的结果是ZYDL。再比如，聚宽拼音一般把晟拼作Cheng，因此象广晟有色会拼成GCYS，而正确的拼法是GSYS。这样的不同之处，大约有30多个。

但pypinyin也有出错的时候，比如重庆港会拼成ZQG。此时，我们就需要使用自定义词典了：

1
2
3
4
5
>>> from pypinyin import load_phrases_dict, lazy_pinyin, Style

>>> load_phrases_dict( {"重庆港": [[u"c"], [u"q"], [u"g"]]}, style=Style.FIRST_LETTER)
>>> lazy_pinyin("重庆港", style=Style.FIRST_LETTER)
['c', 'q', 'g']

由于我们只关心首字母，因此在加载自定义词典时，指定了Style.FIRST_LETTER，这样将只影响后面对此类风格的查询。

如果你想了解哪些拼音聚宽给出的与pypinyin不一样，可以通过下面的代码来检查：

1
2
3
4
5
6
7
8
from pypinyin import Style, lazy_pinyin

for code in await Security.select().eval():
    name = await Security.alias(code)
    jq = await Security.name(code)
    py = "".join(lazy_pinyin(name, style=Style.FIRST_LETTER)).upper()
    if jq != py:
        print(name, py, jq)
  • 需要 2 分钟阅读时间

提速100倍！QMT复权因子高效算法

QMT的XtQuant库提供了量化研究所需要的数据。它在一些API设计上面向底层多一些，应用层在使用时，还往往需要进行一些包装，比如复权就是如此。

这篇文章介绍了将XtQuant的除权信息转换成常常的复权因子的高性能算法。与官方示例相比，速度快了100多倍。

Info

通过XtQuant的API get_market_data_ex，我们可以直接获得经过前后复权处理的行情数据。但是，如果你希望自己使用更高效的方式来存储行情数据的话，就需要存储未复权的原始价格数据和复权因子，在需要使用前后复权价格时，根据选择的时间区间，临时计算复权价格。这就需要也存储复权因子。

XtQuant没有提供复权因子，相反，它通过 get_divid_factors 方法提供了更详尽的分红、送股、配股信息。数据如下所示：

date interest stockBonus stockGift allotNum allotPrice gugai dr
20121019 0.100 0.0 0.0 0.0 0.0 0.0 1.007457
20130620 0.170 0.6 0.0 0.0 0.0 0.0 1.614093
20230614 0.285 0.0 0.0 0.0 0.0 0.0 1.025261


提供的信息非常全，但要利用这些数据来进行价格复权，会比较烦琐。在量化中，多数场合我们可以仅使用复权因子（factor-ratio）来计算前后复权价格。这就需要将上述信息转化为复权因子。

XtQuant的示例中，已经提供了一个由上述信息，计算复权因子的示例。由于它是示例性质的，所以在代码逻辑上需要做到简单易懂，因此它在计算中，使用了循环，而不是向量化的运算方法。

这是官方给出的示例代码:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def gen_divid_ratio(bars, divid_datas):
    drl = []
    dr = 1.0
    qi = 0
    qdl = len(bars)
    di = 0
    ddl = len(divid_datas)
    while qi < qdl and di < ddl:
        qd = bars.iloc[qi]
        dd = divid_datas.iloc[di]
        if qd.name >= dd.name:
            dr *= dd['dr']
            di += 1
        if qd.name <= dd.name:
            drl.append(dr)
            qi += 1
    while qi < qdl:
        drl.append(dr)
        qi += 1
    return pd.DataFrame(drl, index = bars.index, 
                        columns = bars.columns)

# 获取除权信息
dd = xtdata.get_divid_factors(s, start_time="20050104")

# 获取未复权行情
bars = xtdata.get_market_data(field_list, ["000001.SZ"], 
                                '1d', 
                                dividend_type = 'none', 
                                start_time='20050104', 
                                end_time='20240308')
%timeit gen_divid_ratio(bars["close"].T， dd)

这段代码计算了000001.SZ从2005年1月4日以来的复权因子。如果当天没有发生除权，则当天因子从1开始，后面每发生一次除权除息，因子就在前一天的基础上增加dr倍。因此，这样算出来的复权因子，一般情况下是一个以1开始的递增序列。

在notebook中运行时，上述代码的执行时间是407ms±14ms。

下面，我们就介绍如何将其向量化，将速度提升100倍。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
def get_factor_ratio(symbol: str, start: datetime.date, end: datetime.date)->pd.Series:
    """获取`symbol`在`start`到`end`期间的复权因子

    复权因子以EPOCH日为1，依次向后增加。返回值取整个复权因子区间
    中[start, end]这一段。

    Args:
        symbol: 个股代码，以.SZ/.SH等结尾
        start: 起始日期，不得早于EPOCH
        end: 结束日期，不得晚于当前时间

    Returns:
        以日期为index的Series
    """
    if start < tf.int2date(EPOCH):
        raise ValueError(f"start date should not be earlier than {EPOCH}: {start}")

    start_ = tf.date2int(start)
    end_ = tf.date2int(end)
    df = xt.get_divid_factors(symbol, EPOCH)

1
2
3
4
5
6
7
8
    df.index = df.index.astype(int)
    frames = pd.DataFrame([], index=tf.day_frames)
    factor = pd.concat([frames, df["dr"]], axis=1)
    factor.sort_index(inplace=True)
    factor.fillna(1, inplace=True)

    query = f'index >= {start_} and index <= {end_}'
    return factor.cumprod().query(query)["dr"]

我们设置的EPOCH时间是2005年1月4日。这一年是全流通股改启动之年。以此为界，上市公司在治理结构上发生了较大变化，因此，进行量化回测，似乎一般也没必要使用在此之前的数据。

Info

罗马不是一天建成的。股改也是这样。在此后相当长一段时间内，你还能看到一些股票的名字以S开头，意味着该股还未完成股权分置改革。不过，尽管如此，我们也只能以大多数为主。很多人以为量化是一个纯算法的活儿。但是，了解脏数据、处理脏数据，对收益的影响并不比算法少。

这段代码的核心逻辑是，dd['dr']是一个带时间戳的稀疏数据。我们首先要把它展开成：

在此基础上，通过一个cumprod运算，我们就可以求出符合要求的factor ratio。

第一步的运算实际上是一个join运算。我们使用一个在交易日上连续的空的dataframe与上述dd['dr']进行join，其结果就是，如果记录在dd['dr']中存在，就使用dd['dr']中的数值，如果不存在，就使用空值。

然后我们使用pandas.fillna来将所有的空值替换为1.最后，由于我们只需要在[start,end]期间的因子值，所以通过datataframe.query来进行过滤。

上述代码将得到与官方示例一致的结果，但执行时间仅3.96ms±251，比使用循环的版本快了100倍还多。

本方法是作为zillionare接入XtQuant数据的方案的一部分开发的。在这个方案中，我们将采用clickhouse来存放行情数据，以获得更好的回测性能。因此，我们还必须考虑到每种数据如何进行持续更新。这个更新的大致思路是，我们把上述计算中得到的factor ratio存入clickhouse中，在每日更新时，先取得所有股票的factor ratio的最后更新日期(T0)，以此日期为下界，调用xtdata.get_divid_factors来下载最新的除权信息，通过同样的方法求得T0日以来的因子，乘以T0日因子值，即可存入到clickhouse中。

Zillionare接入XtQuant的版本将是2.1，预计在6月发布。

  • 需要 3 分钟阅读时间

后见之明！错过6个涨停之后的复盘

在今年1月2日和1月3日，旅游板块两支个股先后涨停，此后一支月内三倍，另一支连续6个涨停。事后复盘，我们如何在1月2日第一支个股涨停之后，通过量化分析，找出第二支股？

Warning

无论复盘多么精彩，请注意，本文写作的目的只是分享量化技术：如何进行相关性分析。即使本文观点能够策略化，普通人也不具有这样的条件来实施一个量化系统。

一个3倍，一个6连板

这是两支个股在2024年1月17日前60日收盘价图。图中红色虚线是个股启动时间。A大概是受董宇辉小作文、或者尔滨旅游热题材发酵带动，于1月2日率先启动。

尽管A在半个月内股价接近3倍，但从量化的角度，目前还难以精准地实现事件驱动上涨这种类型的建模。但是，如果我们在A启动之后，在1月2日收盘前买入B（就这次而言，B次日开盘仍有买入机会），连续收获6个涨停，也完全可以满意。

现在，我们就来复盘，如何从A涨停，到发现B。

首先，运行策略的时间应该放在14：30分之后，此时对市场进行扫描，找出首板涨停的个股。当日涨停数据在Akshare可以获得，印象中，它能区分首板涨停和连板。

对首板涨停的个股，我们先获取它所在的概念板块。然后对每个板块的成员股进行遍历，通过相关性分析，找到关联度较高的个股。

Tip

概念板块的编制没有严格的规范。有一些软件在编制概念时，甚至允许网友参与。一般地，编制者会从新闻报道、公司报告或者董秘的回答中发掘概念。比如在编制英伟达概念时，如果有人在互动平台上问董秘，你们与英伟达有合作关系吧？董秘回答，我们购买了他们的GPU多少台，这样这家公司就有可能被编入英伟达概念，其实它与英伟达产业链基本上没有什么关系。

与之相反，行业板块的编制相对严谨一些。它是根据公司的主营业务来划分的。

如果仅仅是和龙头同在一个板块是无法保证资金眷顾的。而且，一支个股往往身兼多个概念，在极短的时间里要弄清楚究竟是炒的它的哪一个概念也不容易。不过，通过数据挖掘，我们可以完全不去理会炒作背后的逻辑 -- 何况很多逻辑，根本就是狗p不通。

我们用相关性检测来进行数据挖掘。

相关系数

在概率论和统计学中，相关性(Correlation)显示了两个或几个随机变量之间线性关系的强度和方向。

通常使用相关系数来计量这些随机变量协同变化的程度，当随机变量间呈现同一方向的变化趋势时称为正相关，反之则称为负相关。

我们通过以下公式来计算两个随机变量之间的相关性：

\[ \rho_{XY} = \frac{cov(X, Y)}{\sigma_X\sigma_Y} \]

这样定义的相关系数称作皮尔逊相关系数。一般我们可以通过numpy中的corrcoef，或者scipy.stats.pearsonr来计算。

下面的代码演示了正相关、负相关和不相关的例子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
# x0与x1正相关， 与x2负相关， 与x3分别为不同的随机变量
x0 = np.random.normal(size=100)
x1 = 10* x0 + 1
x2 = -10 * x0 + 1
x3 = np.random.normal(size=100)

x = np.vstack((x0, x1, x2, x3))
rho = np.corrcoef(x)

fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(12, 3))

for i in [0,1,2]:
    ax[i].scatter(x[0,],x[1+i,])
    desc = "Pearson: {:.2f}".format(rho[0,i+1])
    ax[i].title.set_text(desc)
    ax[i].set(xlabel='x',ylabel='y')

plt.show()

绘图时，我们以\(x_0\)为x轴，以\(x_i\)为y轴，如果\(x_0\)与\(x_1\)完全正相关，那么将绘制出一条\(45^。\)向上的直线。这其实就是QQ-Plot的原理。

从左图过渡到右图，只需要在\(x_0\)中不断掺入噪声即可。读者可以自己尝试一下。

皮尔逊相关系数要求只有变量之间是线性相关时，它才能发现这种关联性。很多时候我们必须放宽条件为：标的A上涨，则B也跟着涨。但不管A涨多少，B跟涨又是多少，都不改变它们联系的强度。此时，就要用Spearman相关性。

Tip

无论是皮尔逊相关，还是Spearman，运用在时间序列分析（比如股价）上时，都不完全满足随机变量独立性条件。不过，从经验得知，这种影响还没有大到使它们失去作用的地步。但我们也确实需要了解这一点。有能力啃学术论文的，可以用how-to-use-pearson-correlation-correctly-with-time-series搜索一下stackexchange上的回答。

上面的例子演示的是皮尔逊相关系数的求法，这里使用的是np.corrcoef。它的结果是一个矩阵，所以上例中的变量rho，其取值实际上是：

50%

在这个矩阵中，对角线上的值是自相关系数，显然它们都应该为1。实际上我们要得到时间序列\(s_1\)和\(s_2\)之间的相关系数，应该取\(\rho[0][1]\)，对\(s_1\)和\(s_3\)之间的相关系数，应该取\(\rho[0][2]\)，依次类推，这些可以在代码第13行看到。

我们通过scipy.stats.spearmanr来计算Spearman相关。我们将通过真实的例子来进行演示。

发现强相关个股

假设我们已经拿到了概念板块的个股名单。现在，我们两两计算它们与龙头个股之间的相关性，如果相关系数在0.75以上，我们就认为是强相关，纳入备选池。

相关系数是一个无量纲的数，取值在[-1,1]之间。因此，可以把0.75看成具有75分位的含义

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
async def qqplot(x, y, n=60, end):
    xbars = await Stock.get_bars(x, n, FrameType.DAY, end=end )
    ybars = await Stock.get_bars(y, n, FrameType.DAY, end=end)
    xclose = xbars["close"]
    yclose = ybars["close"]

    pearson = scipy.stats.pearsonr(xclose, yclose)[0]
    spearman = scipy.stats.spearmanr(xclose, yclose).statistic

    if pearson < 0.75:
        return

    a, b = np.polyfit(xclose, yclose, 1)
    ax = plt.subplot(1,1,1)
    ax.scatter(xclose, yclose)
    ax.plot(xclose, a * xclose + b)

    namex = await Security.alias(x)
    namey = await Security.alias(y)
    ax.title.set_text(f'{namex} <=> {namey} pearson: {pearson:.2f} spearman: {spearman:.2f}')
    plt.show()

假设现在是1月2日的下午2时，已经能确认标的A不会开板。现在，我们就拿它与板块内的其它个股逐一计算相关性，排除掉弱相关的个股，因为，既然是弱相关，那么它们就不会跟涨，也不怎么跟跌（在我A，跟跌是必须的）。

当我们使用 pearson > 0.75的判断条件时，在该板块的22支个股中，筛选出5支个股。如果使用spearman > 0.75来判断，则只会选出4支，并且这4支都在pearson筛选出的范围内。这里为排版美观起见，只给出共同的4支：

L50

R50

L50

R50

很幸运，我们要找的标的正在其中。

你肯定想知道另外三支的结果如何。它们有连板吗？有大幅下跌吗？

没有下跌。别忘了，我们是通过相关系数选出来的标的，只要这种关联还存在，即使不跟随上涨，也不应该大幅下跌，不是吗？

实际上，有一支在我们讨论的区间里持平，一支上涨5%，另一支最高上涨16.9%。但如果你有更高的期望，在这个case中，一点点看盘经验可以帮助我们过滤掉另外两只，最终，我们会买入上涨16.9%和6连板的股票。

这个看盘经验是，不要买上方有均线，特别是中长均线的股。这种股在上攻过程中，将会遇到较大的抛压。如果一个很小的板块，资金已经有了一到两个进攻的标的了，是不会有多余的钱来关照这些个股的。

这个策略还有一个很好的卖出条件。如果龙头股一直保持上涨，而个股的关联系数掉出0.75，显然，我们可以考虑卖出。如果龙头股出现滞涨（开盘半小时内不能封住），则也是离场时机。

这一篇我们讨论的是同一板块个股的相关性。如果是处在上下游的两个板块，它们也可能存在相关性，但会有延时。这种情况称作cross correlation。它应该如何计算，又如何使用，也许后面我们会继续探索。

  • 需要 5 分钟阅读时间

量化人如何用好 Jupyter？（二）

当我们使用 Jupyter 时，很显然我们的主要目的是探索数据。这篇文章将介绍如何利用 JupySQL 来进行数据查询--甚至代替你正在使用的 Navicat, dbeaver 或者 pgAdmin。此外，我们还将介绍如何更敏捷地探索数据，相信这些工具，可以帮你省下 90%的 coding 时间。

JupySQL - 替换你的数据库查询工具

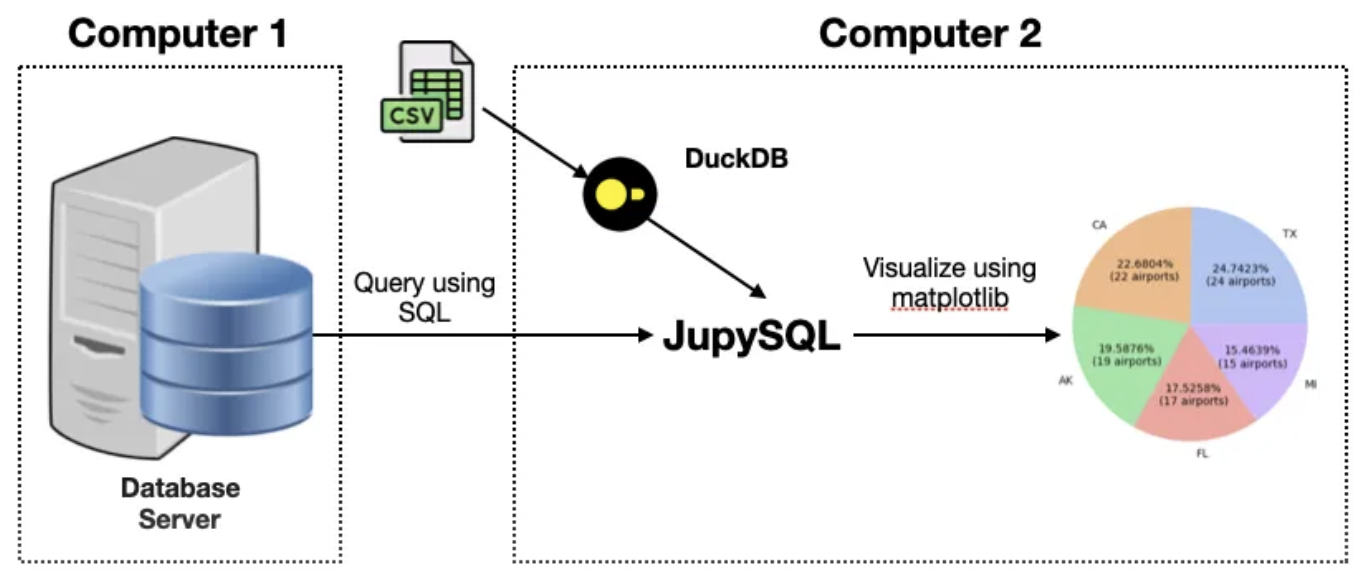
JupySQL 是一个运行在 Jupyter 中的 sql 查询工具。它支持传统关系型数据库（PostgreSQL, MySQL, SQL server）、列数据库（ClickHouse），数据仓库 (Snowflake, BigQuery, Redshift, etc) 和嵌入式数据库 (SQLite, DuckDB) 的查询。

之前我们不得不为每一种数据库寻找合适的查询工具，找到开源、免费又好用的其实并不容易。有一些工具，设置还比较复杂，比如像 Tabix，这是 ClickHouse 有一款开源查询工具，基于 web 界面的。尽管它看起来简单到甚至无须安装，但实际上这种新的概念，导致一开始会引起一定的认知困难。在有了 JupySQL 之后，我们就可以仅仅利用我们已知的概念，比如数据库连接串，SQL 语句来操作这一切。

除了查询支持之外，JupySQL 的另一特色，就是自带部分可视化功能。这对我们快速探索数据特性提供了方便。

安装 JupySQL

现在，打开一个 notebook，执行以下命令，安装 JupySQL:

1
%pip install jupysql duckdb-engine --quiet

之前你可能是这样使用 pip：

1
! pip install jupysql

在前一篇我们学习了 Jupyter 魔法之后，现在你知道了，%pip 是一个 line magic。

显然，JupySQL 要连接某种数据库，就必须有该数据库的驱动。接下来的例子要使用 DuckDB，所以，我们安装了 duckdb-engine。

Info

DuckDB 是一个性能极其强悍、有着现代 SQL 语法特色的嵌入式数据库。从测试上看，它可以轻松管理 500GB 以内的数据，并提供与任何商业数据库同样的性能。

在安装完成后，需要重启该 kernel。

JupySQL 是作为一个扩展出现的。要使用它，我们要先用 Jupyter 魔法把它加载进来，然后通过%sql 魔法来执行 sql 语句：

1
2
3
4
5
6
7
%load_ext sql

# 连接 DUCKDB。下面的连接串表明我们将使用内存数据库
%sql duckdb://

# 这一行的输出结果为 1，表明 JUPYSQL 正常工作了
%sql select 1

数据查询 (DDL 和 DML)

不过，我们来点有料的。我们从 baostock.com 上下载一个 A 股历史估值的示例文件。这个文件是 Excel 格式，我们使用 pandas 来将其读入为 DataFrame，然后进行查询：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
import pandas as pd

df = pd.read_excel("/data/.common/valuation.xlsx")
%load_ext sql

# 创建一个内存数据库实例
%sql duckdb://

# 我们将这个 DATAFRAME 存入到 DUCKDB 中
%sql --persist df

现在，我们来看看，数据库里有哪些表，表里都有哪些字段：

1
2
3
4
5
# 列出数据库中有哪些表
%sqlcmd tables

# 列出表'DF'有哪些列
%sqlcmd columns -t df

最后一行命令将输出以下结果：

name type nullable default autoincrement comment
index BIGINT True None False None
date VARCHAR True None False None
code VARCHAR True None False None
close DOUBLE PRECISION True None False None
peTTM DOUBLE PRECISION True None False None
pbMRQ DOUBLE PRECISION True None False None
psTTM DOUBLE PRECISION True None False None
pcfNcfTTM DOUBLE PRECISION True None False None

作为数据分析师，或者量化研究员，这些命令基本上满足了我们常用的 DDL 功能需求。在使用 pgAdmin 的过程中，要找到一个表格，需要沿着 servers > server > databases > database > Schema > public > Tables 这条路径，一路展开所有的结点才能列出我们想要查询的表格，不免有些烦琐。JupySQL 的命令简单多了。

现在，我们预览一下这张表格：

1
%sql select * from df limit 5

我们将得到如下输出：

index date code close peTTM pbMRQ psTTM pcfNcfTTM
0 2022-09-01 sh.600000 7.23 3.978631 0.370617 1.103792 1.103792
1 2022-09-02 sh.600000 7.21 3.967625 0.369592 1.100739 1.100739
2 2022-09-05 sh.600000 7.26 3.99514 0.372155 1.108372 1.108372
3 2022-09-06 sh.600000 7.26 3.99514 0.372155 1.108372 1.108372
4 2022-09-07 sh.600000 7.22 3.973128 0.370105 1.102266 1.102266

%sql 是一种 line magic。我们还可以使用 cell magic，来构建更复杂的语句：

1
2
3
4
5
# EXAMPLE-1
%%sql --save agg_pe
select code, min(peTTM), max(peTTM), mean(peTTM)
from df
group by code

使用 cell magic 语法，整个单元格都会当成 sql 语句，这也使得我们构建复杂的查询语句时，可以更好地格式化它。这里在%%sql 之后，我们还使用了选项 --save agg_pe，目的是为了把这个较为复杂、但可能比较常用的查询语句保存起来，后面我们就可以再次使用它。

Tip

在 JupySQL 安装后，还会在工具栏出现一个 Format SQL 的按钮。如果一个单元格包含 sql 语句，点击它之后，它将对 sql 语句进行格式化，并且语法高亮显示。

我们通过 %sqlcmd snippets 来查询保存过的查询语句：

1
%sqlcmd snippets

这将列出我们保存过的所有查询语句，刚刚保存的 agg_pe 也在其中。接下来，我们就可以通过%sqlcmd 来使用这个片段：

1
2
3
4
5
6
7
query = %sqlcmd snippets agg_pe

# 这将打印出我们刚刚保存的查询片段
print(query)

# 这将执行我们保存的代码片段
%sql {{query}}

最终将输出与 example-1 一样的结果。很难说有哪一种数据库管理工具会比这里的操作来得更简单！

JupySQL 的可视化

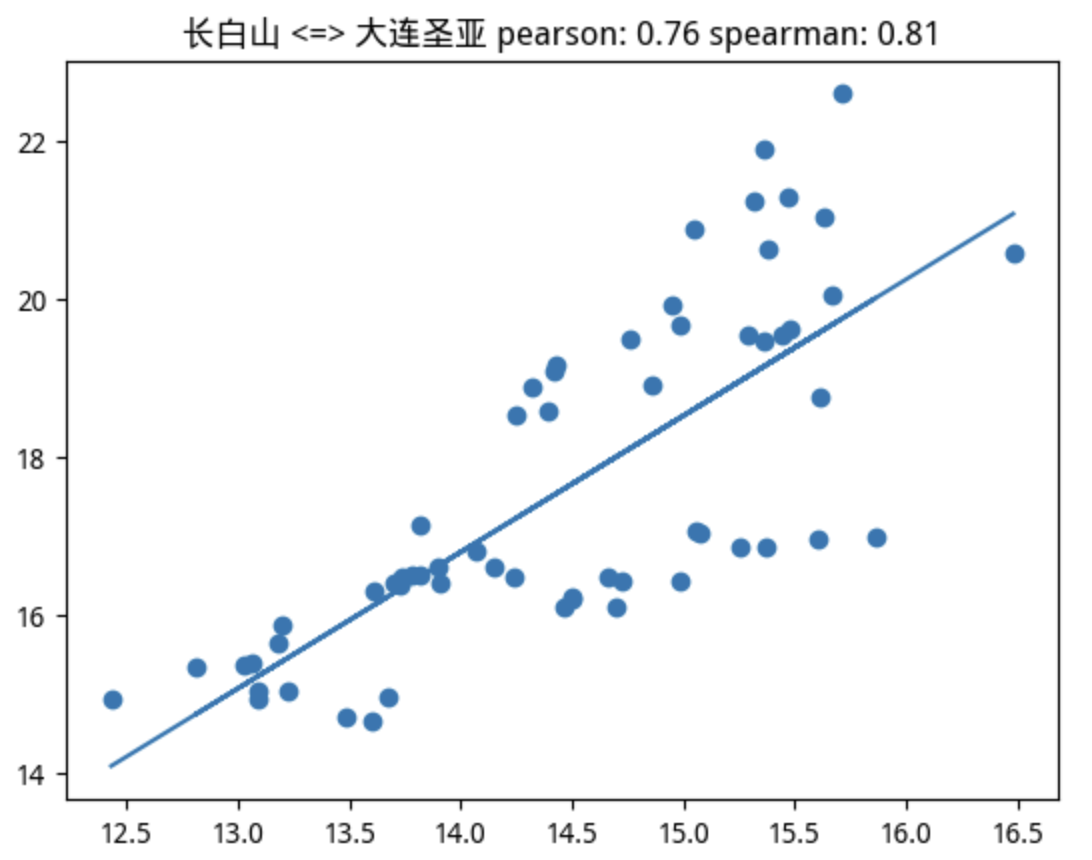
JupySQL 还提供了一些简单的绘图，以帮助我们探索数据的分布特性。

1
%sqlplot histogram -t df -c peTTM pbMRQ

JupySQL 提供了 box, bar, pie 和 histogram。

超大杯的可视化工具

不过，JupyerSQL提供的可视化功能并不够强大，只能算是中杯。有一些专业工具，它们以pandas DataFrame为数据载体，集成了数据修改、筛选、分析和可视化功能。这一类工具有， Qgrid（来自 Quantpian），PandasGUI，D-Tale 和 mitosheet。其中D-Tale功能之全，岂止是趣大杯，甚至可以说是水桶杯。

我们首先探讨的是Qgrid，毕竟出自Quantpian之手，按理说他们可能会加入量化研究员最常用的一些分析功能。 他们在 Youtube 上提供了一个 presentation，介绍了如何使用 Qgrid 来探索数据的边界。不过，随着 QuantPian 关张大吉，所有这些工具都不再有人维护，因此我们也不重点介绍了。

PandasGUI 在 notebook 中启动，但它的界面是通过 Qt 来绘制的，因此，启动以后，它会有自己的专属界面，而且是以独立的 app 来运行。它似乎要求电脑是 Windows。

Mitosheet的界面非常美观。安装完成后，需要重启 jupyterlab/notebook server。仅仅重启 kernel 是不行的，因为为涉及到界面的修改。

重启后，在Notebook的工具条栏，会多出一个“New Mitosheet”的按钮，点击它，就会新增一个单元格，其内容为：

1
2
import mitosheet
mitosheet.sheet(analysis_to_replay="id-sjmynxdlon")

并且自动运行这个单元格，调出 mito 的界面。下面是 mitto 中可视化一例：

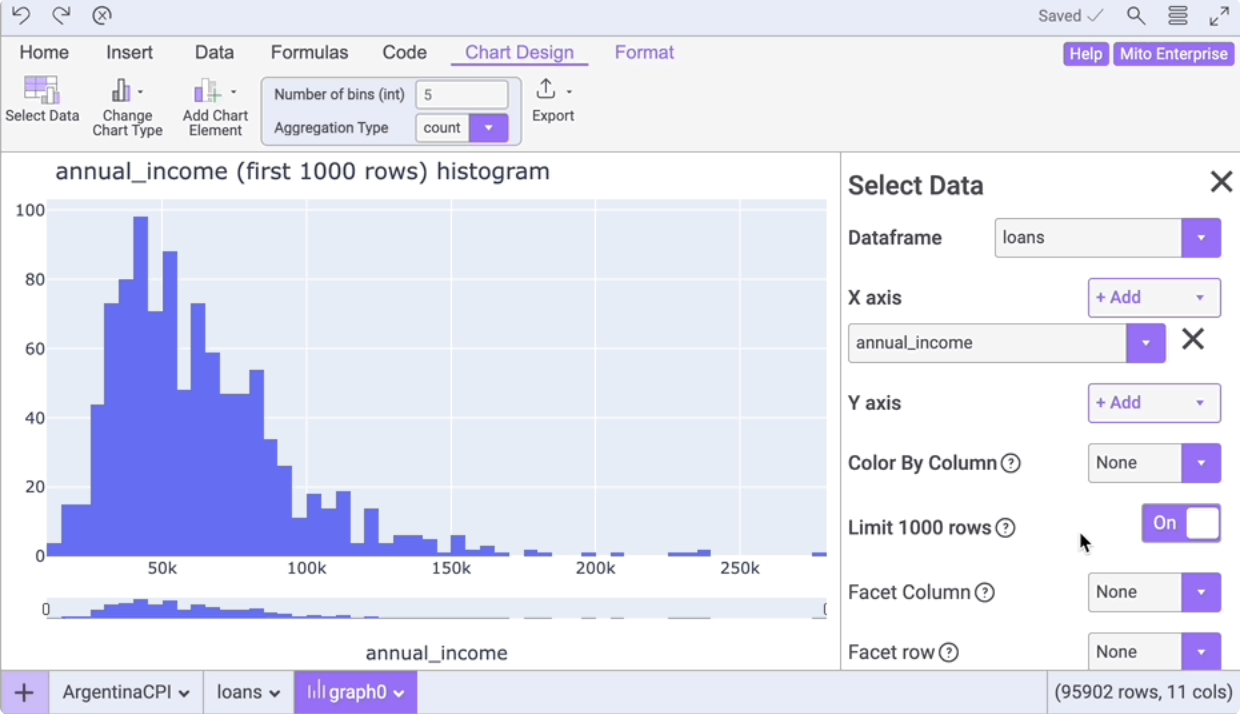
mitto 有免费版和专业版的区分，而且似乎它会把数据上传到服务器上进行分析，所以在国内使用起来，感觉不是特别流畅。

与上面介绍的工具相比，D-Tale 似乎没有这些工具有的这些短板。

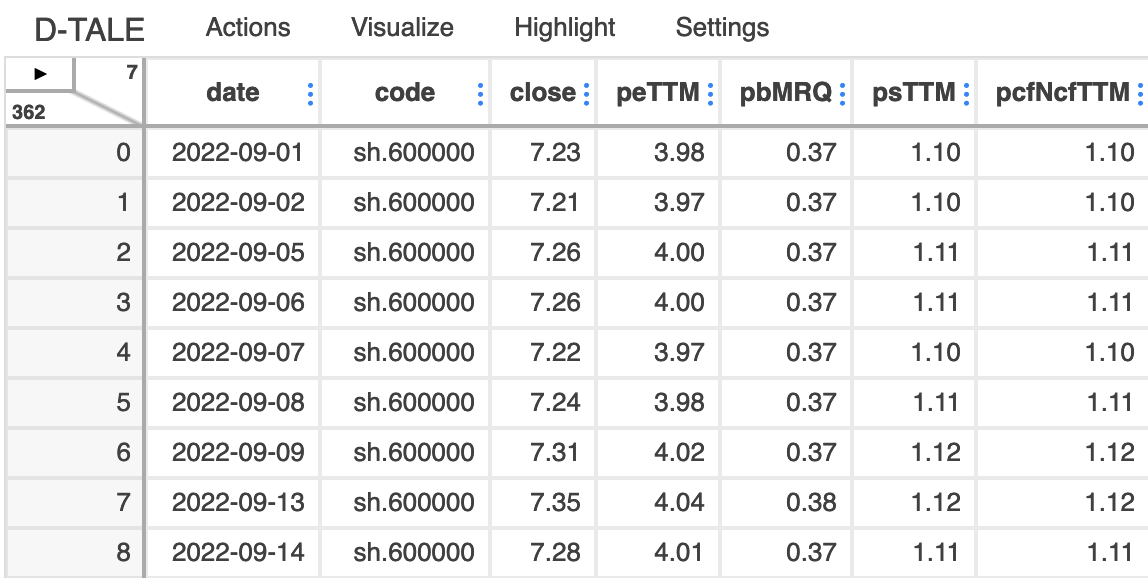
我们在 notebook 中通过pip install dtale来安装 dtale。安装后，重启 kernel。然后执行：

1
2
3
import dtale

dtale.show(df)

这会显加载以下界面：

75%

在左上角有一个小三角箭头，点击它会显示菜单：

75%

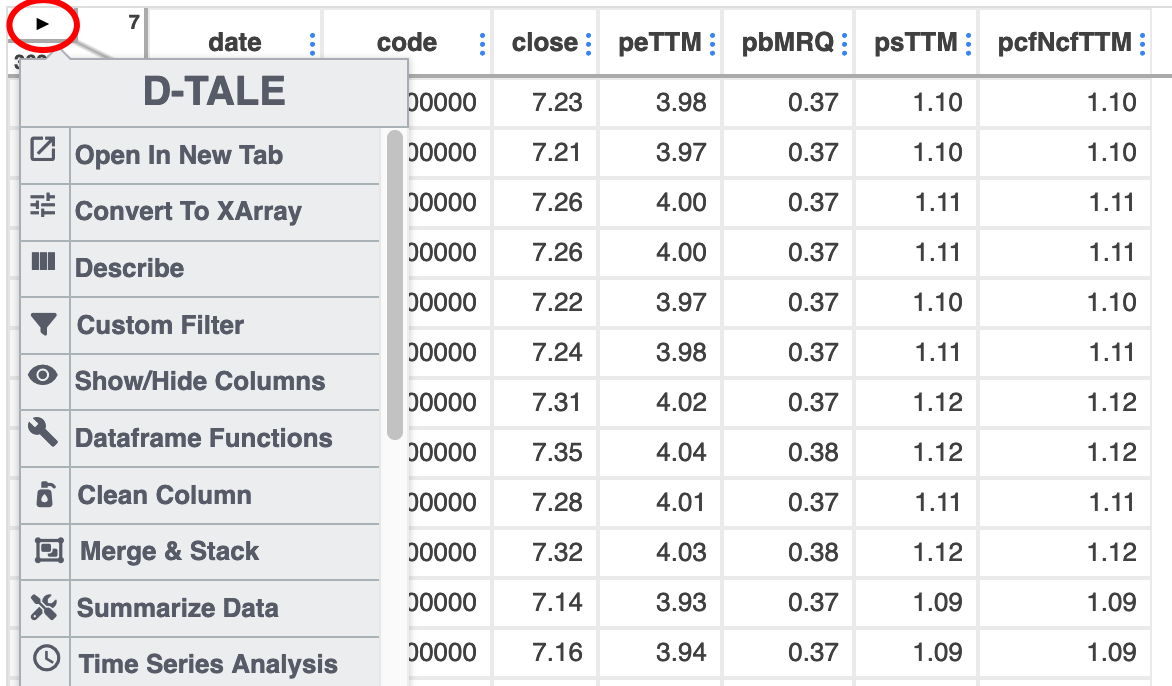
我们点击describe菜单项看看，它的功能要比df.describe 强大不少。df.describe 只能给出均值、4 分位数值，方差，最大最小值，dtale 还能给出 diff, outlier, kurtosis, skew，绘制直方图，Q-Q 图（检查是否正态分布）。

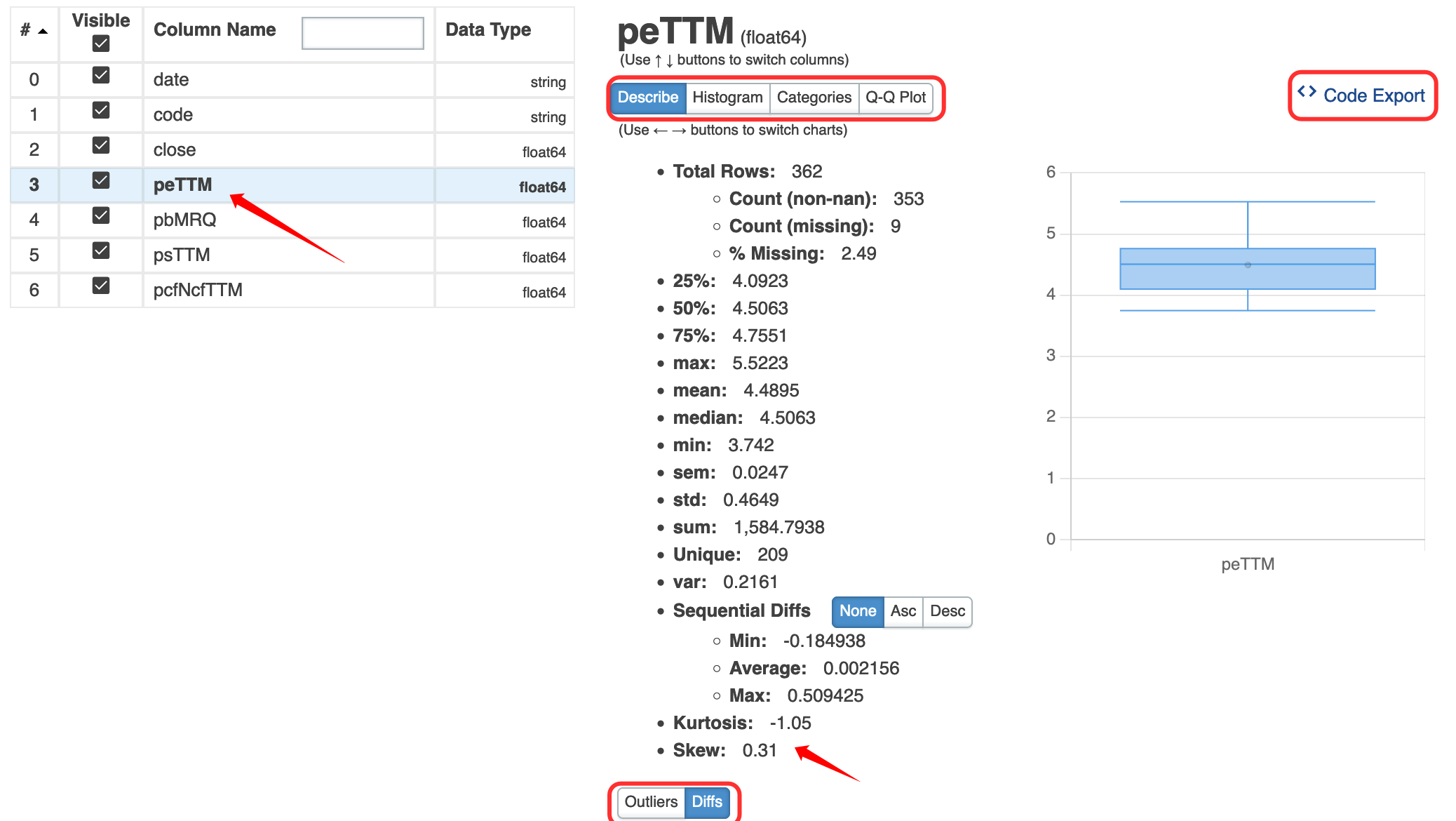
注意我们可以导出进行这些计算所用的代码！这对数据分析的初学者确实很友好。

这是从中导出的绘制 qq 图的代码：

1
2
3
4
5
# DISCLAIMER: 'DF' REFERS TO THE DATA YOU PASSED IN WHEN CALLING 'DTALE.SHOW'

import numpy as np
import pandas as pd
import plotly.graph_objs as go

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
if isinstance(df, (pd.DatetimeIndex, pd.MultiIndex)):
    df = df.to_frame(index=False)

# REMOVE ANY PRE-EXISTING INDICES FOR EASE OF USE IN THE D-TALE CODE, BUT THIS IS NOT REQUIRED
df = df.reset_index().drop('index', axis=1, errors='ignore')
df.columns = [str(c) for c in df.columns]  # update columns to strings in case they are numbers

s = df[~pd.isnull(df['peTTM'])]['peTTM']

import scipy.stats as sts
import plotly.express as px

qq_x, qq_y = sts.probplot(s, dist="norm", fit=False)
chart = px.scatter(x=qq_x, y=qq_y, trendline='ols', trendline_color_override='red')
figure = go.Figure(data=chart, layout=go.Layout({
    'legend': {'orientation': 'h'}, 'title': {'text': 'peTTM QQ Plot'}
}))

有了这个功能，如果不知道如何通过 plotly 来绘制某一种图，那么就可以把数据加载到 dtale，用 dtale 绘制出来，再导出代码。作为量化人，可能最难绘制的图就是 K 线图了。这个功能，dtale 有。

最后，实际上dtale是自带服务器的。我们并不一定要在 notebook 中使用它。安装 dtale 之后，可以在命令行下运行dtale命令，然后再打开浏览器窗口就可以了。更详细的介绍，可以看这份 中文文档。

  • 需要 3 分钟阅读时间

量化人如何用好Jupyter环境？（一）

网上有很多jupyter的使用技巧。但我相信，这篇文章会让你全面涨姿势。很多用法，你应该没见过。

  • 显示多个对象值
  • 魔法：%precision %psource %lsmagic %quickref等
  • vscode中的interactive window

1. 魔法命令

几乎每一个使用过Jupyter Notebook的人，都会注意到它的魔法(magic)功能。具体来说，它是一些适用于整个单元格、或者某一行的魔术指令。

比如，我们常常会好奇，究竟是pandas的刀快，还是numpy的剑更利。在量化中，我们常常需要寻找一组数据的某个分位数。在numpy中，有percentile方法，quantile则是她的pandas堂姊妹。要不，我们就让这俩姐妹比一比身手好了。有一个叫timeit的魔法，就能完成这任务。

不过，我们先得确定她们是否真有可比性。

1
2
3
4
5
6
7
8
import numpy as np
import pandas as pd

array = np.random.normal(size=1_000_000)
series = pd.Series(array)

print(np.percentile(array, 95))
series.quantile(0.95)

两次输出的结果都是一样，说明这两个函数确实是有可比性的。

在上面的示例中，要显示两个对象的值，我们只对前一个使用了print函数，后一个则省略掉了。这是notebook的一个功能，它会默认地显示单元格最后输出的对象值。这个功能很不错，要是把这个语法扩展到所有的行就更好了。

不用对神灯许愿，这个功能已经有了！只要进行下面的设置：

1
2
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

在一个单独的单元格里，运行上面的代码，之后，我们就可以省掉print:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
import numpy as np
import pandas as pd

array = np.random.normal(size=1_000_000)
series = pd.Series(array)

# 这一行会输出一个浮点数
np.percentile(array, 95)

# 这一行也会输出一个浮点数
series.quantile(0.95)

这将显示出两行一样的数值。这是今天的第一个魔法。

现在，我们就来看看，在百万数据中探囊取物，谁的身手更快一点？

1
2
3
4
5
6
7
8
import numpy as np
import pandas as pd

array = np.random.normal(size=1_000_000)
series = pd.Series(array)

%timeit np.percentile(array, 95)
%timeit series.quantile(0.95)

我们使用%timeit来测量函数的运行时间。其输出结果是：

1
2
26.7 ms ± 5.67 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
21.6 ms ± 837 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

看起来pandas更快啊。而且它的性能表现上更稳定，标准差只有numpy的1/7。mean±std什么的，量化人最熟悉是什么意思了。

这里的timeit，就是jupyter支持的魔法函数之一。又比如，在上面打印出来的分位数，有16位小数之多，真是看不过来啊。能不能只显示3位呢？当然有很多种方法做到这一点，比如，我们可以用f-str语法：

1
f"{np.percentile(array, 95):.3f}"

啰哩啰嗦的，说好要Pythonic的呢?不如试试这个魔法吧：

1
2
%precision 3
np.percentile(array, 95)

之后每一次输出浮点数，都只有3位小数了，是不是很赞？

如果我们在使用一个第三方的库，看了文档，觉得它还没说明白，想看它的源码，怎么办?可以用psource魔法：

1
2
3
from omicron import tf

%psource tf.int2time

这会显示tf.int2time函数的源代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
    @classmethod
    def int2time(cls, tm: int) -> datetime.datetime:
        """将整数表示的时间转换为`datetime`类型表示

        examples:
            >>> TimeFrame.int2time(202005011500)
            datetime.datetime(2020, 5, 1, 15, 0)

        Args:
            tm: time in YYYYMMDDHHmm format

        Returns:
            转换后的时间
        """
        s = str(tm)
        # its 8 times faster than arrow.get()
        return datetime.datetime(
            int(s[:4]), int(s[4:6]), int(s[6:8]), int(s[8:10]), int(s[10:12])
        )

看起来Zillionare-omicron的代码，文档还是写得很不错的。能和numpy一样，在代码中包括示例，并且示例能通过doctest的量化库，应该不多。

Jupyter的魔法很多，记不住怎么办？这里有两个魔法可以用。一是%lsmagic：

1
%lsmagic

这会显示为：

确实太多魔法了！不过，很多命令是操作系统命令的一部分。另一个同样性质的魔法指令是%quickref，它的输出大致如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
IPython -- An enhanced Interactive Python - Quick Reference Card
================================================================

obj?, obj??      : Get help, or more help for object (also works as
                   ?obj, ??obj).
?foo.*abc*       : List names in 'foo' containing 'abc' in them.
%magic           : Information about IPython's 'magic' % functions.

Magic functions are prefixed by % or %%, and typically take their arguments
without parentheses, quotes or even commas for convenience.  Line magics take a
single % and cell magics are prefixed with two %%.

Example magic function calls:
...

输出内容大约有几百行，一点也不quick!

2. 在vscode中使用jupyter

R50

如果有可能，我们应该尽可能地利用vscode的jupyter notebook。vscode中的jupyter可能在界面元素的安排上弱于浏览器（即原生Jupyter），比如，单元格之间的间距太大，无法有效利用屏幕空间，菜单命令少于原生jupyter等等。但仍然vscode中的jupyter仍然有一些我们难于拒绝的功能。

首先是代码提示。浏览器中的jupyter是BS架构，它的代码提示响应速度比较慢，因此，只有在你按tab键之后，jupyter才会给出提示。在vscode中，代码提示的功能在使用体验上与原生的python开发是完全一样的。

其次，vscode中的jupyter的代码调试功能更好。原生的Jupyter中进行调试可以用%pdb或者%debug这样的magic，但体验上无法与IDE媲美。上图就是在vscode中调试notebook的样子，跟调试普通Python工程一模一样地强大。

还有一点功能是原生Jupyter无法做到的，就是最后编辑位置导航。

如果我们有一个很长的notebook，在第100行调用第10行写的一个函数时，发现这个函数实现上有一些问题。于是跳转到第10行进行修改，修改完成后，再回到第100行继续编辑，这在原生jupyter中是通过快捷键跳转的。

通常我们只能在这些地方，插入markdown cell,然后利用标题来进行快速导航，但仍然无法准确定位到具体的行。但这个功能在IDE里是必备功能。我们在vscode中编辑notebook，这个功能仍然具备。

notebook适于探索。但如果最终我们要将其工程化，我们还必须将其转换成为python文件。vscode提供了非常好的notebook转python文件功能。下面是本文的notebook版本转换成python时的样子：

转换后的notebook中，原先的markdown cell，转换成注释，并且以# %% [markdown]起头；而原生的python cell，则是以# %%起头。

vscode编辑器会把这些标记当成分隔符。每个分隔符，引起一个新的单元格，直到遇到下一个分隔符为止。这些单元格仍然是可以执行的。由于配置的原因，在我的工作区里，隐藏了这些toolbar,实际上它们看起来像下图这样。

66%

这个特性被称为Python Interactive Window，可以在vscode的文档vscode中查看。

我们把notebook转换成python文件，但它仍然可以像notebook一样，按单元格执行，这就像是个俄罗斯套娃。宇宙第一的IDE，vs code实至名归。

  • 需要 4 分钟阅读时间

为什么量化人应该使用duckdb？

上一篇笔记介绍了通过duckdb，使用SQL进行DataFrame的操作。我们还特别介绍了它独有的 Asof Join 功能，由于量化人常常处理跨周期行情对齐，这一功能因此格外实用。但是duckdb的好手段，不止如此。

  • 完全替代sqlite，但命令集甚至超过了Postgres
  • 易用性极佳
  • 性能怪兽

作为又一款来自人烟稀少的荷兰的软件，北境这一苦寒之地，再一次让人惊喜。科技的事儿，真是堆人没用。

  • 需要 3 分钟阅读时间

给Pandas找个搭子，用SQL玩转Dataframe!

对有一定SQL基础的人来说，pandas中的查询会有点繁琐。

在这篇文章，我们将给Pandas找个搭子，在用SQL方便的地方，我们用SQL；在用原生查询方便的地方，我们就用原生查询。

这个搭子会是谁呢？

  • 需要 2 分钟阅读时间

来自世坤！寻找Alpha 构建交易策略的量化方法

问：常常看到有人说Alpha seeking，这究竟是什么意思？

自己回答不如推荐一本书：《Finding Alphas: A Quantitative Approach to Building Trading Strategies》，它的题目正好就是寻找Alpha。我拿到的PDF是2019年的第二版。来自WorldQuant（世坤）的Igor Tulchinshky等人，Igor Tulchinshky是世坤的创始人。