在我们的《因子分析与机器学习策略》课程中,提供了从2005年到2023年,长达18年的日线数据(共1100多万条记录)供学员进行因子挖掘与验证。最初,我们是通过functools中的lru_cache装饰器,将数据缓存到内存中的。这样一来,除了首次调用时时间会略长(比如,5秒左右)外,此后的调用都是毫秒级的。
但这样也带来一个问题,就是内存占用太大。一次因子分析课程可能会占用5G以上。由于Jupyterlab没有自动关闭idle kernel的能力(这一点在google Colab和kaggle中都有),我们的内存很快就不够用了。
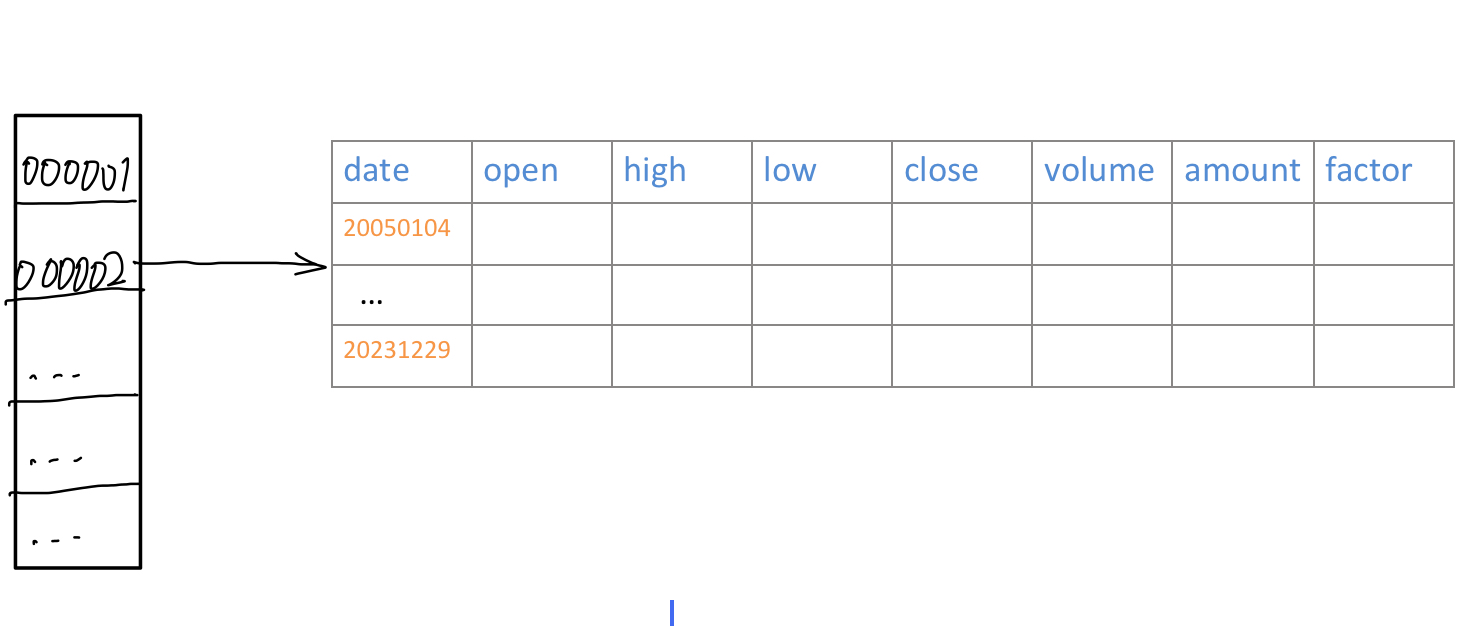
我们的数据是以字典的方式组织,并保存在磁盘上的:
每支股票的键值是股票代码,对应值则是一个Numpy structured array。这样的数据结构看上去比较独特,不过我们稍后就能看到这样组织的原因。
在进行因子分析之前,用户可能会通过指定universe,以及起止时间来加载行情数据。所谓Universe,就是指一个股票池。用户可能有给定的证券列表,也可能只想指定universe的规模;起止时间用来切换观察的时间窗口,这可能是出于性能的考虑(最初进行程序调试时,只需要用一小段行情数据;调试完成后则需要用全部数据进行回测,或者分段观察)。
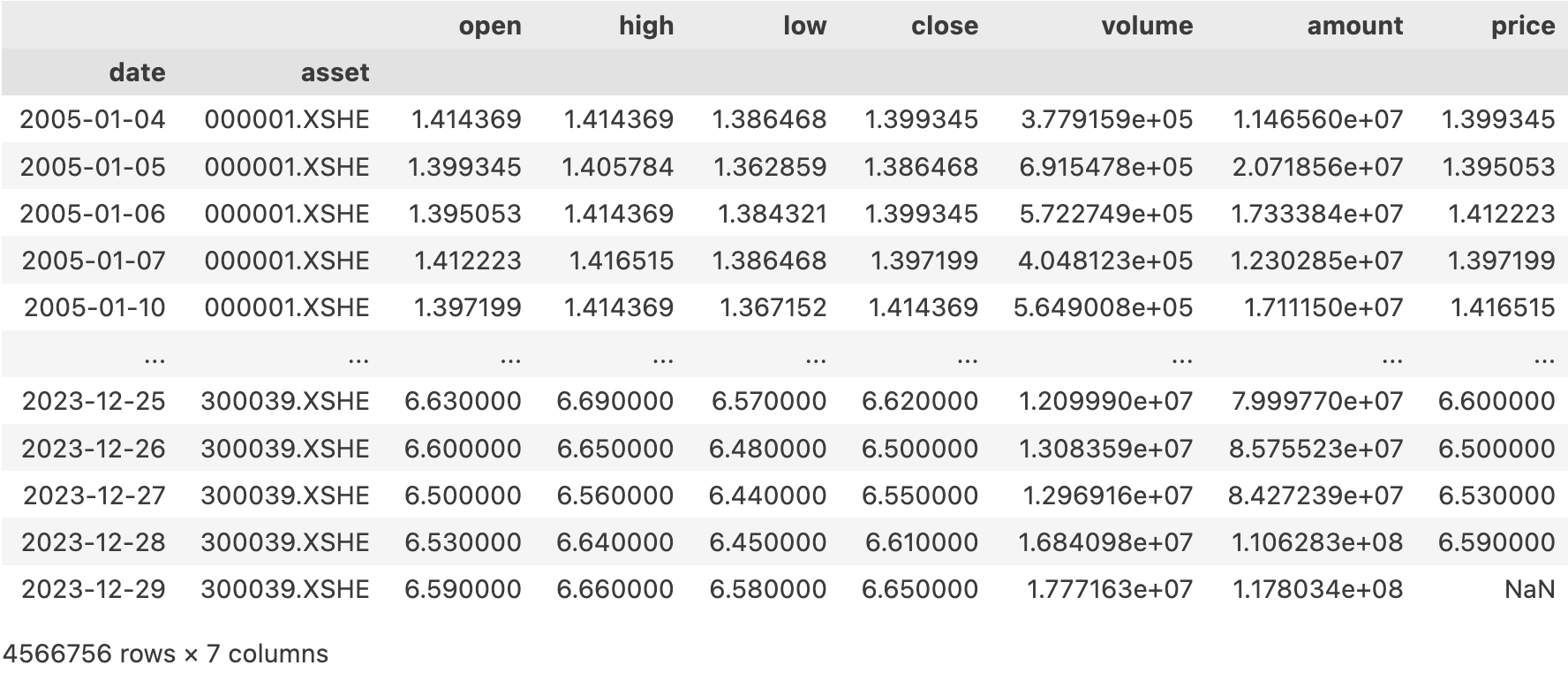
最终,它要返回一个DataFrame,以date和asset(即股票代码)为双重索引,包含了OHLC,volume等列,并且这些列要根据end进行前复权(这种复权方式称为动态前复权)。此外,还将包含一个amount列,这一列则无须复权。
因此,这个函数的签名是:
| def load_bars(start_date:datetime.date,
end_date:datetime.date,
universe: Tuple[str]|int = 500)->pd.DataFrame:
pass
|
学员的学习过程是阅读我们的notebook文档,并尝试单元格中的代码,也可能修改这些代码再运行。因此,这是一个交互式的操作,一般来说,只要用户的等待时间不超过3秒,都是可以接受的。如果响应速度低于1秒,则可以认为是理想的。
去掉缓存后,最初的一个实现的运行速度大致是5秒:
| start = datetime.date(2023, 12,1)
end = datetime.date(2023, 12,31)
%time load_bars(start, end, 2000)
|
后面的测试将使用现样的参数。
当然,如果使用更大的universe,则时间还会加长。
由于这个结果超过了3秒,所以,希望能对代码进行一些优化。性能优化是编程中比较有难度的例子,因为它涉及到对程序运行原理的理解,涉及到对多个技术栈的掌握。在这个过程中我探索了Deep Seek R1的能力边界,可供大家参考。
最初的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | def load_bars_v1(
start: datetime.date, end: datetime.date, universe: Tuple[str]|int = 500
)->pd.DataFrame:
if barss is None:
with open(os.path.join(data_home, "bars_1d_2005_2023.pkl"), "rb") as f:
barss = pickle.load(f)
keys = list(barss.keys())
if isinstance(universe, int):
if universe == -1:
selected_keys = keys
else:
selected_keys = random.sample(keys, min(universe, len(keys)))
try:
pos = selected_keys.index("000001.XSHE")
swp = selected_keys[0]
selected_keys[0] = "000001.XSHE"
selected_keys[pos] = swp
except ValueError:
selected_keys[0] = "000001.XSHE"
else:
selected_keys = universe
dfs = []
for symbol in selected_keys:
qry = "frame >= @start & frame <= @end"
df = pd.DataFrame(barss[symbol]).assign(asset=symbol).query(qry)
if len(df) == 0:
logger.debug("no bars for %s from %s to %s", symbol, start, end)
continue
# 前复权
last = df.iloc[-1]["factor"]
adjust_factor = df["factor"] / last
adjust = ["open", "high", "low", "close", "volume"]
df.loc[:, adjust] = df.loc[:, adjust].multiply(adjust_factor, axis="index")
dfs.append(df)
df = pd.concat(dfs, ignore_index=True)
df.set_index(["frame", "asset"], inplace=True)
df.index.names = ["date", "asset"]
df.drop("factor", axis=1, inplace=True)
df["price"] = df["open"].shift(-1)
return df
|
代码已进行了相当的优化(其中部分也基于AI建议)。比如,将数据保存为字典,先按universe进行筛选,再拼接为dataframe,而不是将所有数据保存为dataframe,通过pandas来按universe进行筛选(将花费数倍时间)。
此外,在进行前复权时,它使用了multiply方法,从而可以一次对多个列进行前复权操作,这一建议正是AI给出来的。
但是,代码中还存在一个for loop,如果消除了这个循环,是否能进一步提升速度呢?
下面,我就使用Deep Seek R1进行尝试。
这是第一轮的prompt:
Quote
我有一个dataframe,以date和asset为联合索引,有open, high, low, close, volume, amount和factor等列。其中factor是复权因子。
现在,要对该数据结构实现以下功能:
1. 筛选出asset 在 selected_symbols列表中,date在[start, end]中的记录
2. 对这些记录,按asset进行分组,然后对 open, high, low, close, volume进行前复权。
3. 结果用dataframe返回,索引仍为date/asset,列为复权后的open, high,low, close, volume字段,以及未处理的amount。
请分别给出基于pandas, pyarrow, polars, duckdb的实现,并建议性能最优的一个。
Deep Seek的思考过程很长,这里略过了。我们直接看它的答案。磁盘读写对速度的影响并不大,所以,我们先把数据从磁盘中加载出来,保存到barss中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | with open(os.path.join(data_home, "bars_1d_2005_2023.pkl"), "rb") as f:
data = pickle.load(f)
dfs = []
for symbol, bars in data.items():
df = pd.DataFrame(bars)
df["asset"] = symbol
df = df.rename(columns={"frame": "date"})
dfs.append(df)
barss = pd.concat(dfs,ignore_index=True).set_index(["date", "asset"]).sort_index()
print(len(barss))
# 定义一个一致的universe,便于比较
universe = barss.index.get_level_values("asset").unique().tolist()
|
以下的代码都出自于 Deep Seek。我们让它对最耗时的筛选和复权部分给出方案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | def adjust_pandas(df, selected_symbols, start, end):
# 筛选数据
idx = pd.IndexSlice
filtered = df.loc[idx[start:end, selected_symbols], :]
# 按 asset 分组计算最后复权因子
grouped = filtered.groupby('asset', group_keys=False)
last_factor = grouped['factor'].transform('last')
# 计算调整比例
ratio = filtered['factor'] / last_factor
# 计算复权后字段
adjusted = filtered.assign(
open = filtered['open'] * ratio,
high = filtered['high'] * ratio,
low = filtered['low'] * ratio,
close = filtered['close'] * ratio,
volume = filtered['volume'] * (last_factor / filtered['factor'])
)
# 选择最终列并保持索引
return adjusted[['open', 'high', 'low', 'close', 'volume', 'amount']]
%time adjust_pandas(barss, universe, start, end)
adjust_pandas(barss, universe, start, end)
|
尽管我对Pandas很熟悉了,但仍有一些API是不知道的,比如transform。但运用正确的API,恰恰是 Python中提升性能的关键一招。
这个版本的平均运行时长是7秒。说明pandas的筛选确实很慢。
我们略过pyarrow的版本。pyarrow版本的运行时间大致是3.7秒左右。比原始版本只略有进步。这里也看出python 3.11中,for loop的运行速度已经很快了。
这是它给出的polars的版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | import polars as pl
def adjust_polars(df, selected_symbols, start, end):
# 筛选数据
filtered = df.filter(
(pl.col("date").is_between(start, end)) &
(pl.col("asset").is_in(selected_symbols))
)
# 计算最后复权因子和调整比例
adjusted = filtered.with_columns(
last_factor = pl.col("factor").last().over("asset")
).with_columns(
ratio = pl.col("factor") / pl.col("last_factor"),
volume_ratio = pl.col("last_factor") / pl.col("factor")
).with_columns(
open = pl.col("open") * pl.col("ratio"),
high = pl.col("high") * pl.col("ratio"),
low = pl.col("low") * pl.col("ratio"),
close = pl.col("close") * pl.col("ratio"),
volume = pl.col("volume") * pl.col("volume_ratio")
)
# 选择最终列
return adjusted.select(["date", "asset", "open", "high", "low", "close", "volume", "amount"])
adjust_polars(barss, universe, start, end)
|
之前我并不熟悉Polars,Deep Seek一下子扩展了我的能力边界。如果我要通过自学,然后来实现这部分功能,我不知道要多久才能发现.over这个API,因为这是 Polars 独有的一个窗口运算API,我无法把知识从我熟悉的Pandas中迁移过来。
但是,这个版本有一个错误:它没有遵从我给的数据格式,而是把barss当成了一个有asset和date列的polars DataFrame。通过使用通义灵码,修正了此错误,修正后的代码如下:
| %time adjust_polars(pl.from_pandas(barss.reset_index()), universe, start, end)
|
得到的运行速度是1.01秒,已很接近我们要求的理想速度了。
现在,我们来看它给出的duckdb的版本:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | import duckdb
def adjust_duckdb(df, selected_symbols, start, end):
query = f"""
SELECT
date, asset,
open * (factor / last_factor) AS open,
high * (factor / last_factor) AS high,
low * (factor / last_factor) AS low,
close * (factor / last_factor) AS close,
volume * (last_factor / factor) AS volume,
amount
FROM (
SELECT
*,
LAST_VALUE(factor) OVER (
PARTITION BY asset
ORDER BY date
ROWS BETWEEN UNBOUNDED PRECEDING AND UNBOUNDED FOLLOWING
) AS last_factor
FROM df
WHERE
asset IN ({','.join([f"'{s}'" for s in selected_symbols])})
AND date BETWEEN '{start}' AND '{end}'
)
"""
return duckdb.query(query).to_df()
adjust_duckdb(barss, universe, start, end)
|
这里也会出现一个类似的错误,即查询语句需要df中存在asset, date列,但它们却出现在索引中。我们略作修正即可运行:
| %time adjust_duckdb(barss.reset_index(), universe, start, end)
|
最终运行速度是1.21秒,在这个例子中略慢于polars,在所有方案中排在第二(在另一台机器,使用机械阵列硬盘时,更强的CPU时, duckdb更快)。但是,duckdb方案在数据规模上可能更有优势,即,如果数据集再大一到两个量级,它很可能超过polars。
在polars与duckdb中,需要的都是扁平结果的数据结构(即asset/date不作为索引,而是作为列字段存在),因此,我们可以考虑将数据结构进行重构,使用apache parquet格式写入到磁盘中,这样可以保存整个方案耗时仍保持在1秒左右。
Info
据说急急如律令要翻译成为 quickly, quickly, biu biu biu 😁
在前面,我们代替Deep Seek做了很多思考,是因为担心它对代码的最终执行速度没有sense。现在,我们试一下,直接抛出最终问题,看看会如何:
Quote
我有一个dataframe,以date和asset为联合索引,有open, high, low, close, volume, amount和factor等列。其中factor是复权因子。
现在,要对该数据结构实现以下功能:
- 筛选出asset 在 selected_symbols列表中,date在[start, end]中的记录
- 对这些记录,按asset进行分组,然后对 open, high, low, close, volume进行前复权。
- 结果用dataframe返回,索引仍为date/asset,列为复权后的open, high,low, close, volume字段,以及未处理的amount。
输入数据是1000万条以上,时间跨度是2005年到2023年,到2023年底,大约有5000支股票。输出结果将包含2000支股票的2005年到2023年的数据。请给出基于python,能在1秒左右实现上述功能的方案。
这一次,我们只要求技术方案限定在Python领域内,给了Deep Seek极大的发挥空间。
Deep Seek不仅给出了代码,还给出了『评测报告』,认为它给出的方案,能在某个CPU+内存组合上达到我们要求的速度。
Deep Seek认为,对于千万条记录级别的数据集,必须使用像parallel pandas这样的库来进行并行化才能达成目标。事实上这个认知是错误的。
这一次Deep Seek给出的代码可运行度不高,我们没法验证基于并行化之后,速度是不是真的更快了。不过,令人印象深刻的是,它还给出了一个performance benchmark。这是它自己GAN出来的,还是真有人做过类似的测试,或者是从类似的规模推导出来的,就不得而知了。
重要的是,在给了Deek Seek更大的自由发挥空间之后,它找出了之前在筛选时,性能糟糕的重要原因: asset是字符串类型!
在海量记录中进行字符串搜索是相当慢的。在pandas中,我们可以将整数转换为category类型,此后的筛选就快很多了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | import pyarrow as pa
import pyarrow.parquet as pq
data_home = os.path.expanduser(data_home)
origin_data_file = os.path.join(data_home, "bars_1d_2005_2023.pkl")
with open(origin_data_file, 'rb') as f:
data = pickle.load(f)
dfs = []
for symbol, bars in data.items():
df = pd.DataFrame(bars)
df["asset"] = symbol
df = df.rename(columns={"frame": "date"})
dfs.append(df)
barss = pd.concat(dfs,ignore_index=True)
barss['asset'] = barss['asset'].astype('category')
print(len(barss))
table = pa.Table.from_pandas(barss)
parquet_file_path = "/tmp/bars_1d_2005_2023_category.parquet"
with open(parquet_file_path, 'wb') as f:
pq.write_table(table, f)
|
现在,我们再来看polars或者duckdb的方案的速度:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | import polars as pl
def adjust_polars(df, selected_symbols, start, end):
# 筛选数据
filtered = df.filter(
(pl.col("date").is_between(start, end)) &
(pl.col("asset").is_in(selected_symbols))
)
# 计算最后复权因子和调整比例
adjusted = filtered.with_columns(
last_factor = pl.col("factor").last().over("asset")
).with_columns(
ratio = pl.col("factor") / pl.col("last_factor"),
volume_ratio = pl.col("last_factor") / pl.col("factor")
).with_columns(
open = pl.col("open") * pl.col("ratio"),
high = pl.col("high") * pl.col("ratio"),
low = pl.col("low") * pl.col("ratio"),
close = pl.col("close") * pl.col("ratio"),
volume = pl.col("volume") * pl.col("volume_ratio")
)
# 选择最终列
return adjusted.select([pl.col("date"), pl.col("asset"), pl.col("open"), pl.col("high"), pl.col("low"), pl.col("close"), pl.col("volume"), pl.col("amount")])
# 示例调用
start = datetime.date(2005, 1, 1)
end = datetime.date(2023, 12, 31)
barss = pl.read_parquet("/tmp/bars_1d_2005_2023_category.parquet")
universe = random.sample(barss['asset'].unique().to_list(), 2000)
%time adjust_polars(barss, universe, start, end)
|
结果是只需要91ms,令人印象深刻。duckdb的方案需要390ms,可能是因为我们需要在Python域拼接大量的selected_symbols字符串的原因。
借助 Deep Seek,我们把一个需要5秒左右的操作,加速到了0.1秒,速度提升了50倍。
本文测试都在一台mac m1机器上运行,RAM是16GB。当运行在其它机器上,因CPU,RAM及硬盘类型不同,数据表现甚至排名都会有所不同_。
这次探索中,仅从解决问题的能力上看,Deep Seek、通义和豆包都相当于中级程序员,即能够较好地完成一个小模块的功能性需求,它情绪稳定,细微之处的代码质量更高。
当我们直接要求给出某个数据集下,能达到指定响应速度的Python方案时,Deep Seek有点用力过猛。从结果上看,如果我们通过单机、单线程就能达到91ms左右的响应速度,那么它给出的多进程方案,很可能是要劣于这个结果的。Deep Seek只是遵循了常见的优化思路,但它没有通过实际测试来修正自己的方案。
这说明,它们还无法完全替代人类程序员,特别是高级程序员:对于AI给出的结果,我们仍然需要验证、优化甚至是推动AI向前进,而这刚好是高级程序员才能做到的事情。
但这也仅仅是因为AI还不能四处走动的原因。因为这个原因,它不能像人类一样,知道自己有哪些测试环境可供方案验证,从而找出具体环境下的最优方案。
在铁皮机箱以内,它是森林之王,人类无法与之较量。但就像人不能拔着自己的头发离开地球一样,它的能力,也暂时被封印在铁皮机箱之内。但是,一旦它学会了拔插头,开电源,高级程序员的职业终点就不再是35岁,而是AI获得自己的莲花肉身之时。
至于初中级程序员,目前看是真不需要了。1万元的底薪,加上社保,这能买多少token? 2025年的毕业生,怎么办?



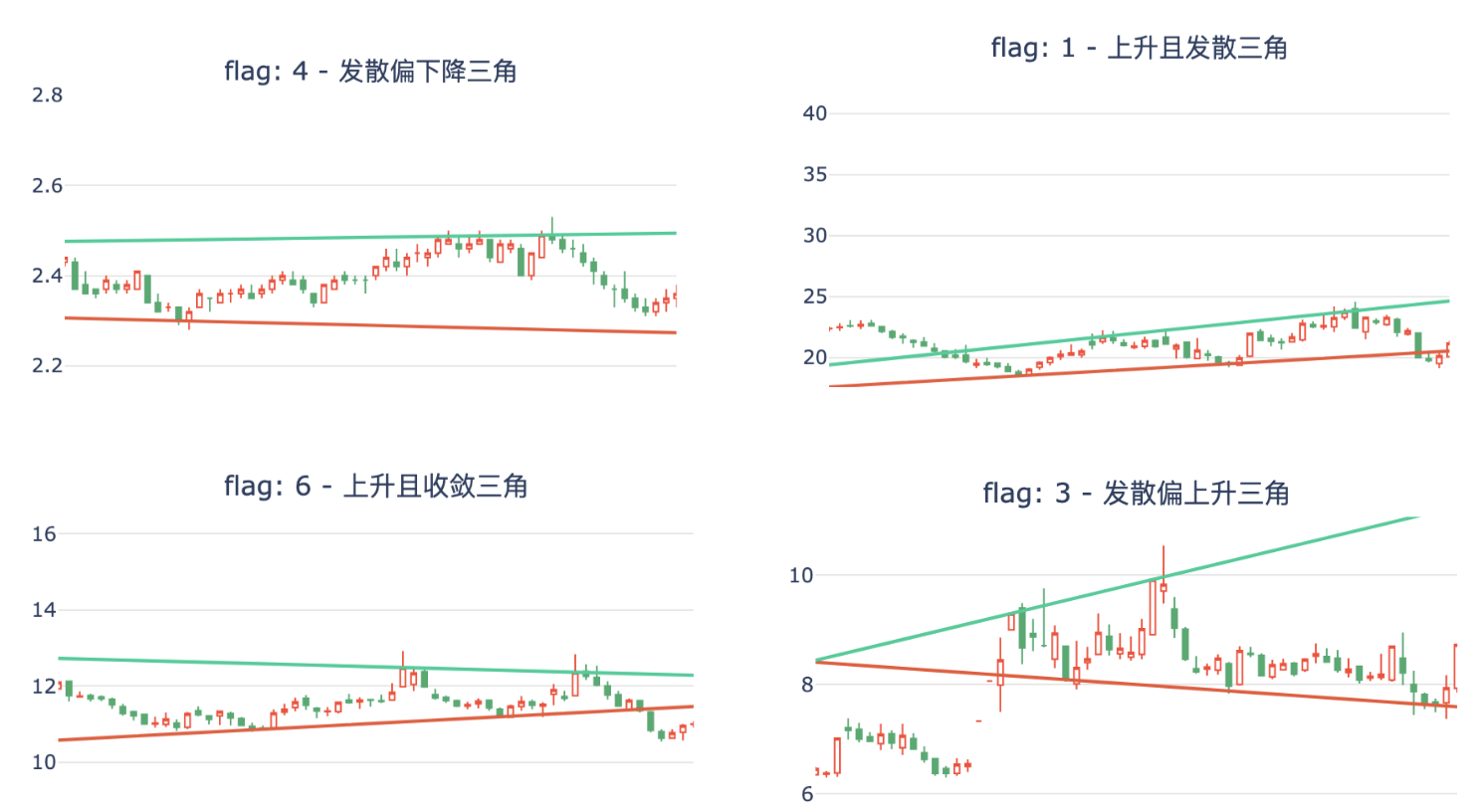

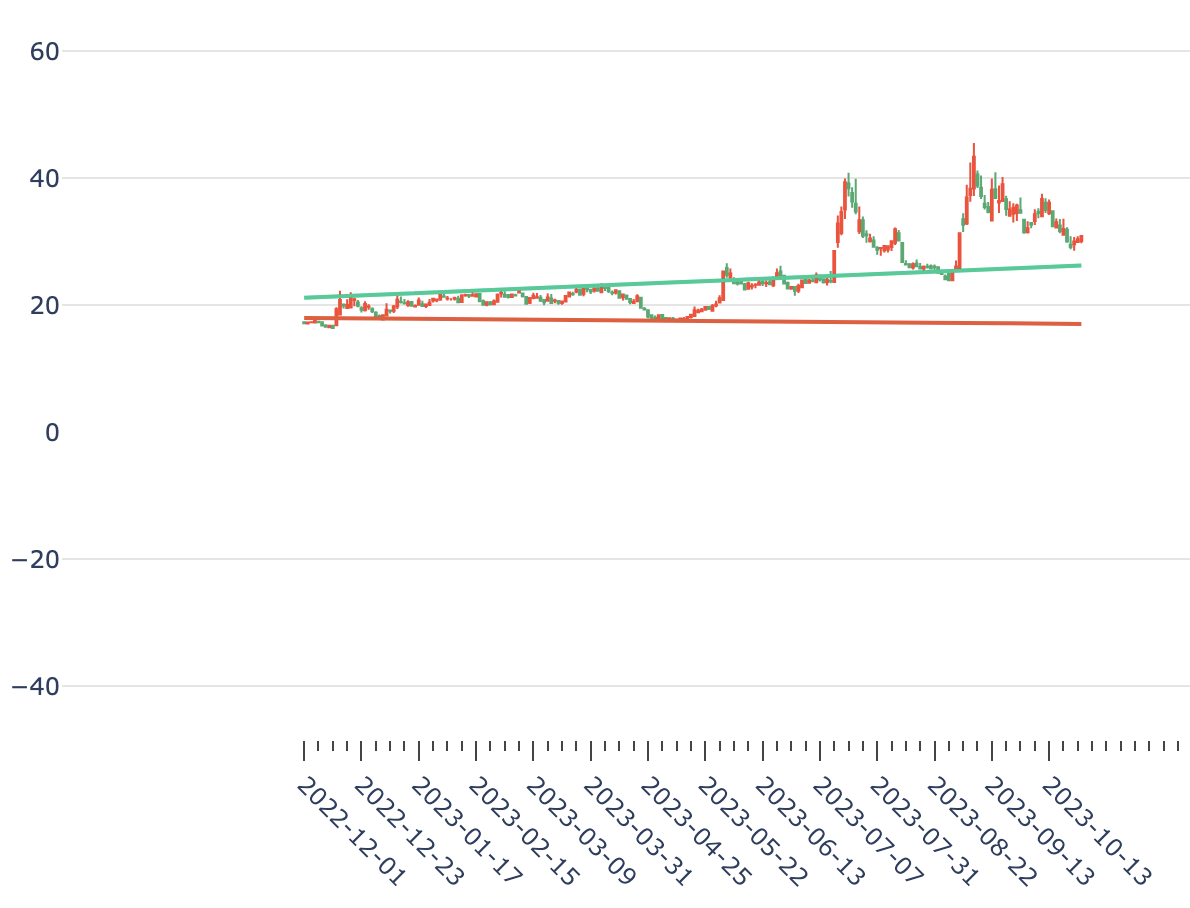
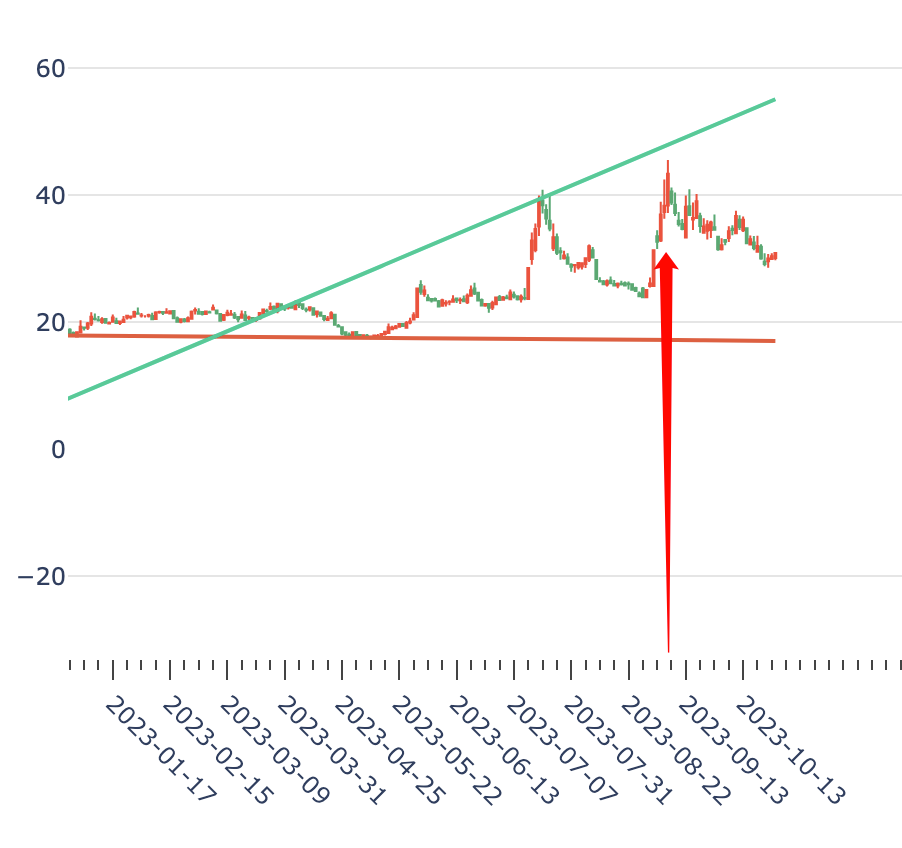
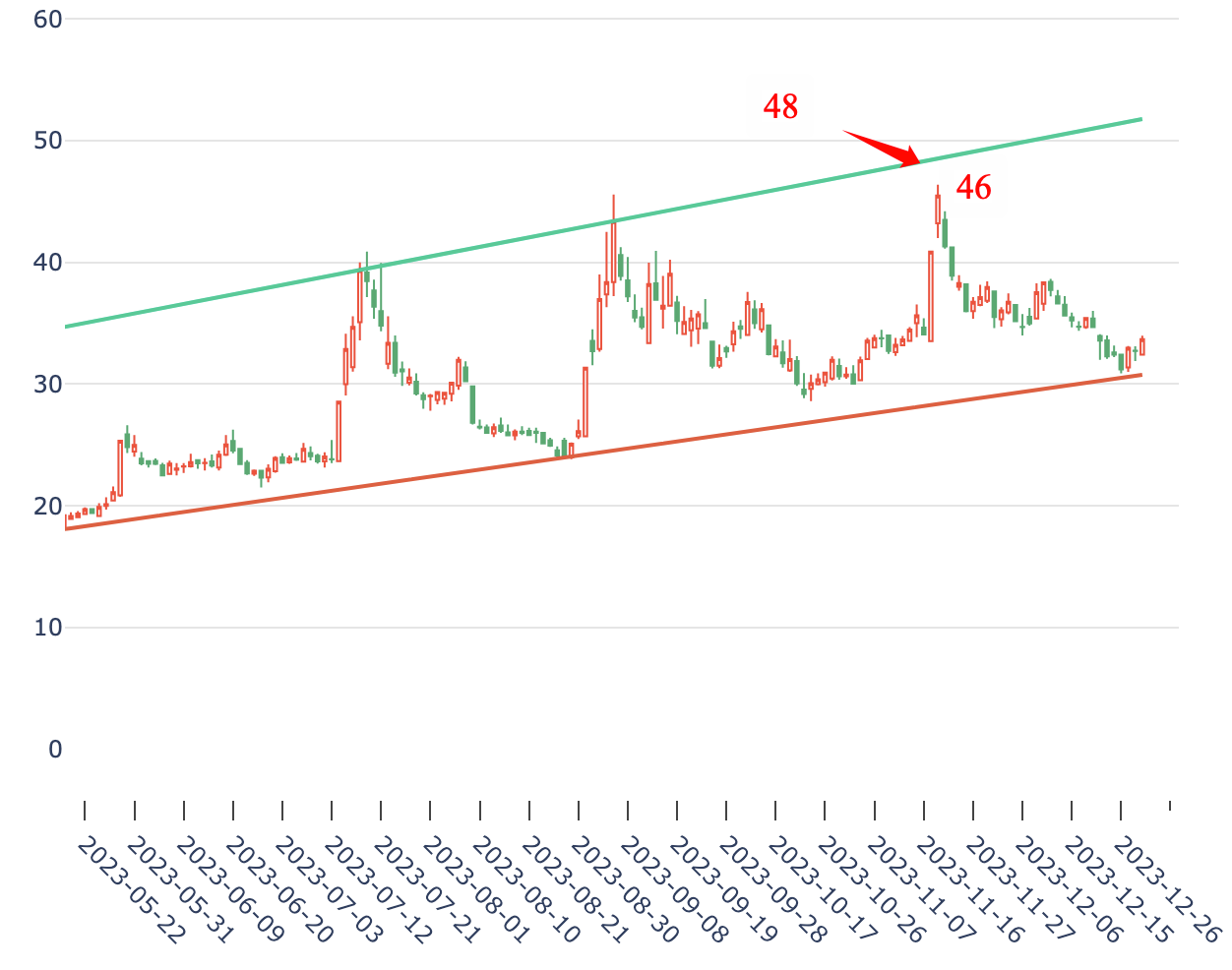
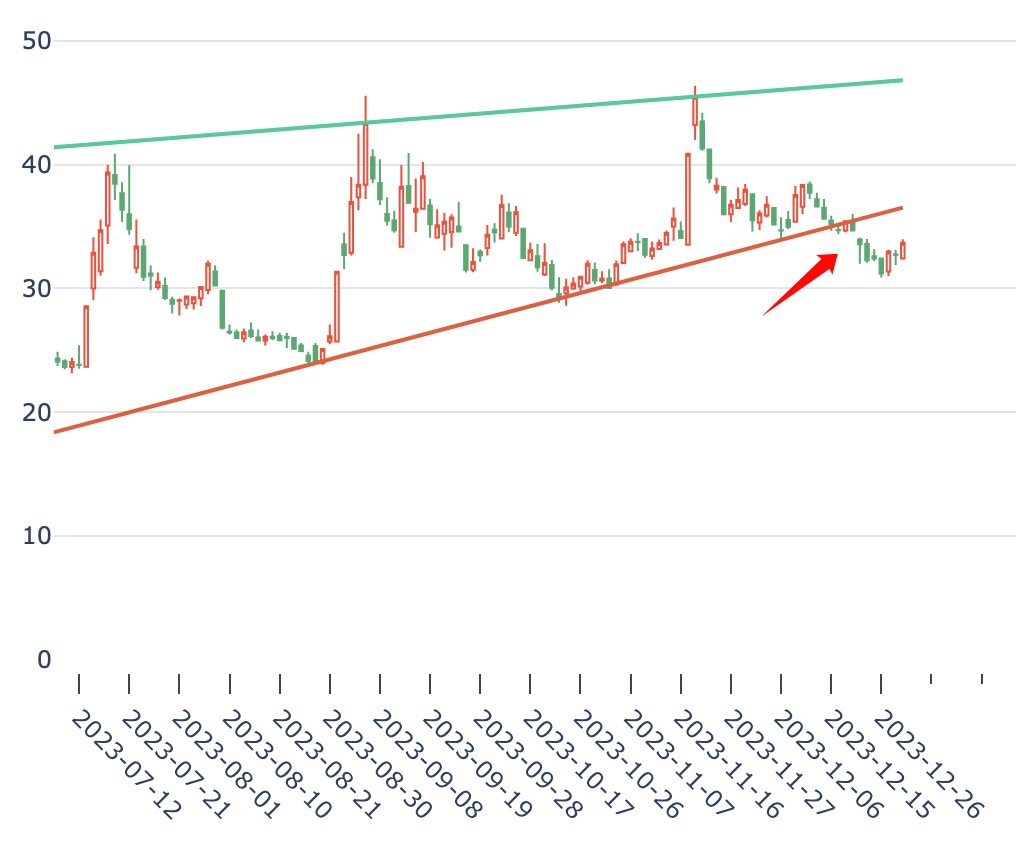
 前篇文章提到可以用HDBSCAN算法来来对资产进行聚类,在聚类完成之后,对聚类结果进行协整检验,通过计算对冲比,可以构造成平稳序列。我们知道一个平稳时间序列的均值、方差恒定并且有自协相关特性,那么,一旦它偏离了均值,迟早都会回归到均值上。利用这一点,可以生成交易信号。
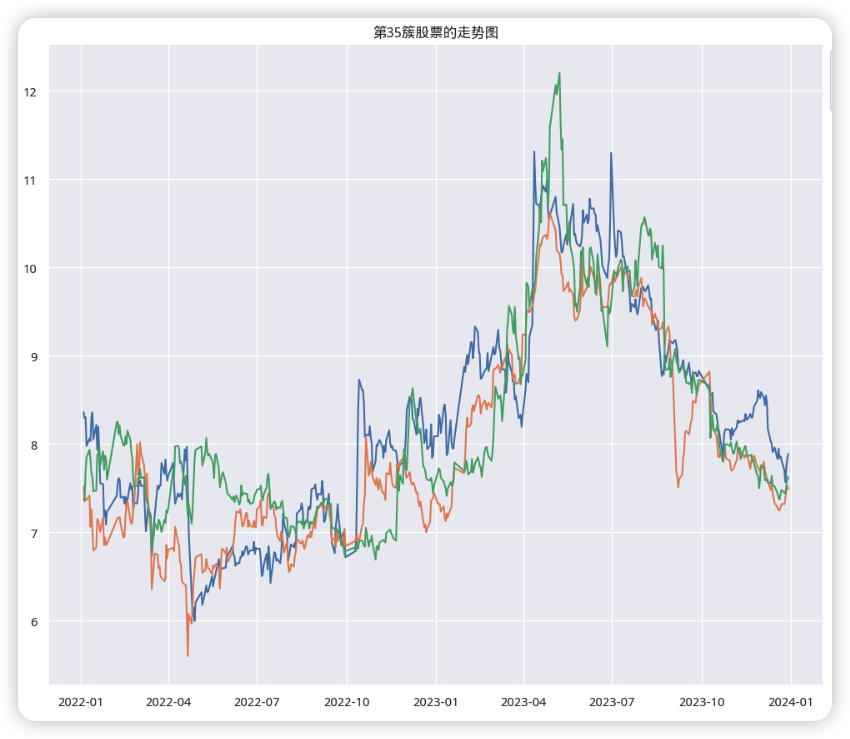
前篇文章提到可以用HDBSCAN算法来来对资产进行聚类,在聚类完成之后,对聚类结果进行协整检验,通过计算对冲比,可以构造成平稳序列。我们知道一个平稳时间序列的均值、方差恒定并且有自协相关特性,那么,一旦它偏离了均值,迟早都会回归到均值上。利用这一点,可以生成交易信号。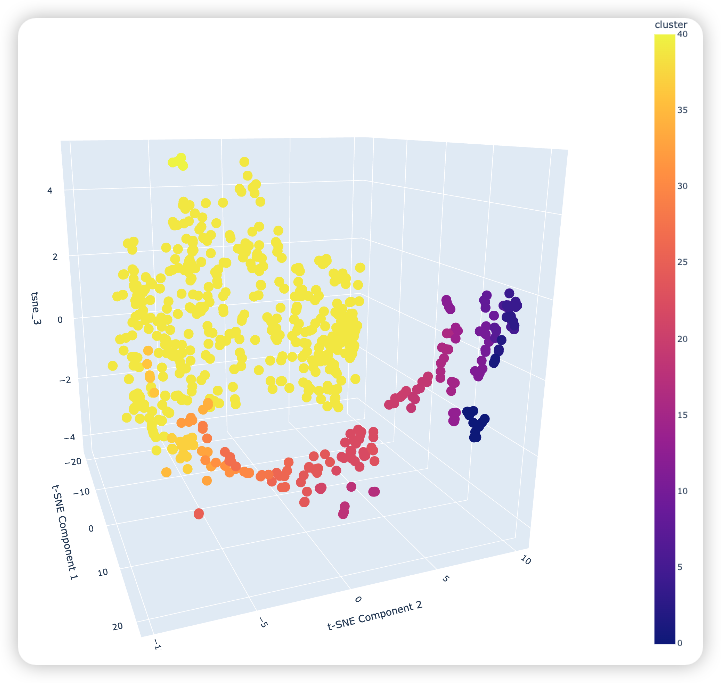
 那是否可以继续用HDBSCAN聚类算法对2022年10月份之前的数据进行聚类,看上面的3支股票是否也被分在了一起。还是上面的代码,只是将时间改为了2022年1月1日到2022年10月1日,运行后得到下面的3D图:
那是否可以继续用HDBSCAN聚类算法对2022年10月份之前的数据进行聚类,看上面的3支股票是否也被分在了一起。还是上面的代码,只是将时间改为了2022年1月1日到2022年10月1日,运行后得到下面的3D图:
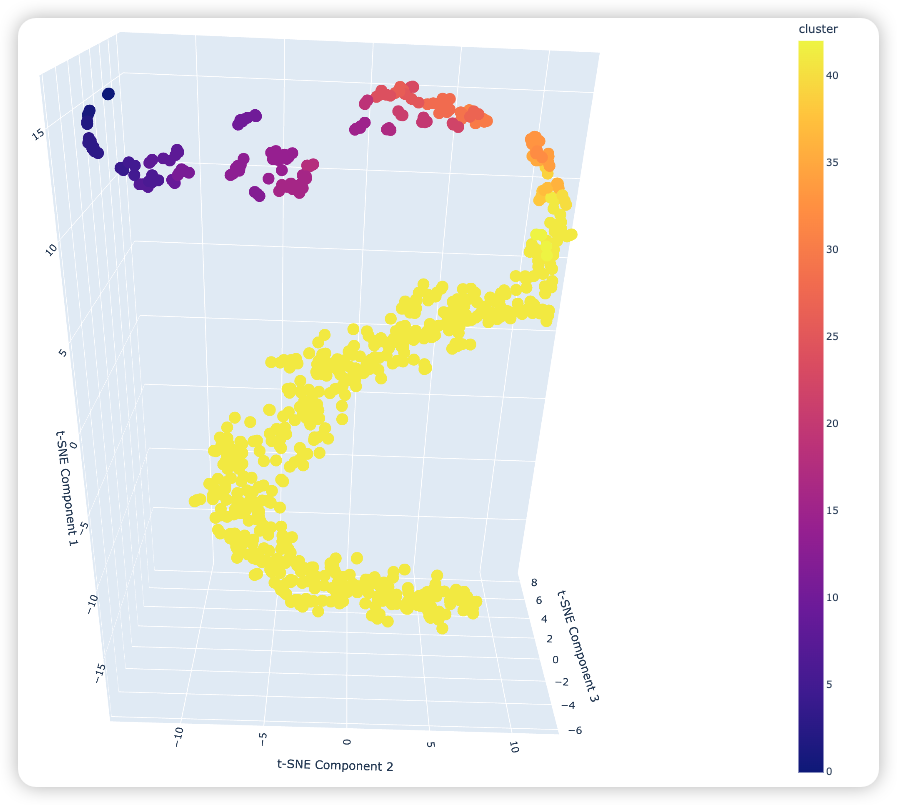
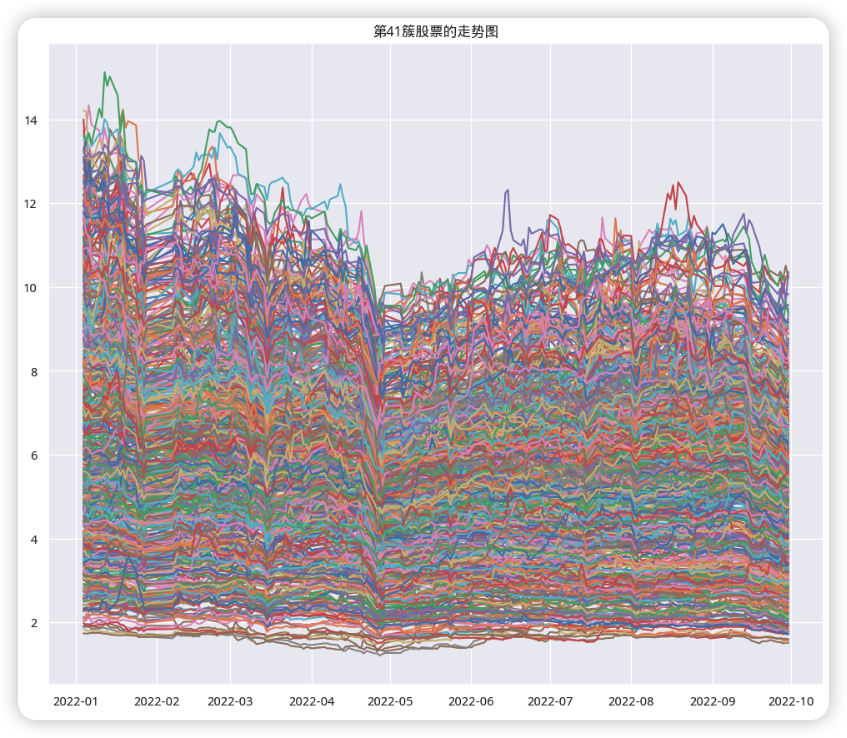 我们想要知道的是这三支股票在持续上升之前会有什么特征,虽然这一个大类里面的股票数据有点多,但观察上面的趋势图可以知道它们的走势大致是相同的,所以才会被分为一类。那继续将这600多支股票在用HDBSCA进行聚类,之前的3支股票会不会被分为一类?也就是说需要验证3支股票在持续上升前的大致趋势也是一致。感兴趣的读者可以自己尝试一下,下面是小编验证的结论:
对这600支股票重新在2022年1月到2022年10月进行聚类,总共被分成了三类,之前的那三支股票有2支被分在了一簇,另外一支在另一类里面。这个结果我认为足以说明这600支股票在2022年1月到2022年10月之间的趋势是相似的,所以600多支股票只被分为三类。
我们想要知道的是这三支股票在持续上升之前会有什么特征,虽然这一个大类里面的股票数据有点多,但观察上面的趋势图可以知道它们的走势大致是相同的,所以才会被分为一类。那继续将这600多支股票在用HDBSCA进行聚类,之前的3支股票会不会被分为一类?也就是说需要验证3支股票在持续上升前的大致趋势也是一致。感兴趣的读者可以自己尝试一下,下面是小编验证的结论:
对这600支股票重新在2022年1月到2022年10月进行聚类,总共被分成了三类,之前的那三支股票有2支被分在了一簇,另外一支在另一类里面。这个结果我认为足以说明这600支股票在2022年1月到2022年10月之间的趋势是相似的,所以600多支股票只被分为三类。
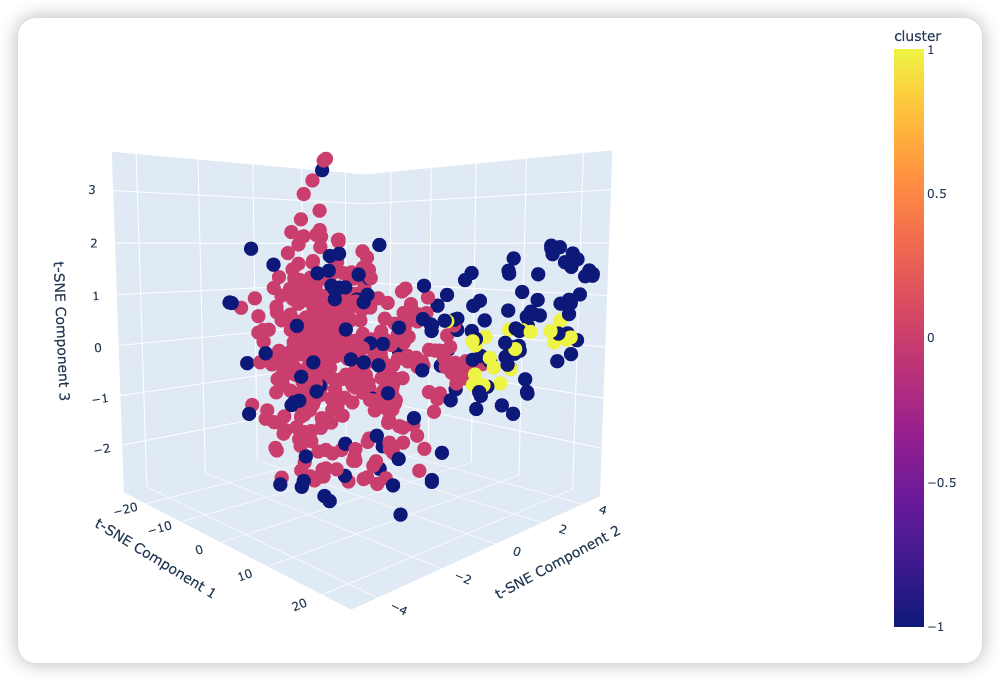 所以,HDBSCAN算法对选股是有效的,它选出来的一类趋势类似,所以可以用前一篇内容中构造这一类股票的平稳序列来产生交易信号。
所以,HDBSCAN算法对选股是有效的,它选出来的一类趋势类似,所以可以用前一篇内容中构造这一类股票的平稳序列来产生交易信号。