跳转至


课程  因子投资  机器学习  story  量化传奇  Python  Poetry  ppw  算法  hdbscan  聚类  选股  Algo  minimum  numpy  algo  FFT  模式识别  配对交易  GBDT  LightGBM  XGBoost  statistics  CDF  KS-Test  回测  过拟合  algorithms  machine learning  strategy  python  sklearn  Info  interview  career  xgboost  PCA  wavelet  Figures  Behavioral Economics  人物  职场  Quantopian  figure  Banz  rsi  zigzag  穹顶压力  因子  pe  ORB  策略  Xgboost  factor  alpha101  alpha  技术指标  wave  quant  algorithm  pearson  spearman  因子分析  Alphalens  涨停板  herd-behaviour  因子策略  momentum  因子评估  review  trade  history  indicators  zscore  波动率  顶背离  freshman  resources  others  AI  DeepSeek  network  tools  weekly  pandas  quantlib  jupyter-notebook  pypinyin  qmt  xtquant  blog  static-site  duckdb  工具  colors  free resources  barra  world quant  Alpha  pdf  openbb  数据  arsenal  copilot  vscode  code  量化数据存储  hdf5  h5py  programming  cursor  augment  trae  Jupyter  jupysql  pyarrow  parquet  数据源  实盘  clickhouse  notebook  Numpy  Pandas 


Index

  • 需要 3 分钟阅读时间

机器的觉醒！人工智能风云激荡70年

机器学习是人工智能的一个子集。人工智能是指使计算机系统能够执行通常需要人类智能才能完成的任务的技术和方法。人工智能涵盖了多种技术和子领域，如机器学习、深度学习、自然语言处理、计算机视觉、专家系统等。

人工智能的概念正式提出是在1956年达特矛斯的夏季人工智能研究会上。达特矛斯学院(Dartmouth College)虽小，但却是常春藤大学之一。这次会议由约翰·麦卡锡发起，克劳德.香农等人参与了研讨会。约翰·麦卡锡是计算机科学家和认知科学家，也是人工智能学科的创始人之一。他还是著名的编程语言Lisp的发明者，早期许多人工智能系统和算法都是用Lisp语言编写的。

达特茅斯AI研讨会

发起会议的约翰·麦卡锡最初认为，只要集中全美最好的几位科学家，大概只要8周就能攻克人工智能问题。不想从1956年发起的宏伟梦想，经过近70年的筚路褴褛，今天仍然只能算是半道其中。

这一路上，就像是光的微粒说与波动说的争论一样，关于人工智能的发展方向，也一直存在两种主要的思想，即人工智能应该基于规则还是基于数据来构建模型？两种思想之间的争斗跌宕起伏，最终在三位华人科学家的加持下，数据派占据了上风，同时铸就了当代人工智能波澜壮阔的发展。

人工智能最先从仿生学得到启发。1890年代，Santiago Ramón Cajal(圣地亚哥·拉蒙·卡哈尔)提出了神经元学说，后来被Camillo Golgi（Camillo Golgi）通过高尔基染色法所证实。1943年，Warren MeCulloch(沃伦.麦卡洛克)和Walter Pitts（沃尔特.皮茨）将复杂的神经元电化学过程简化为相对简单的信号交换[^activation]，最终为人工智能仿生打下坚实的基础。

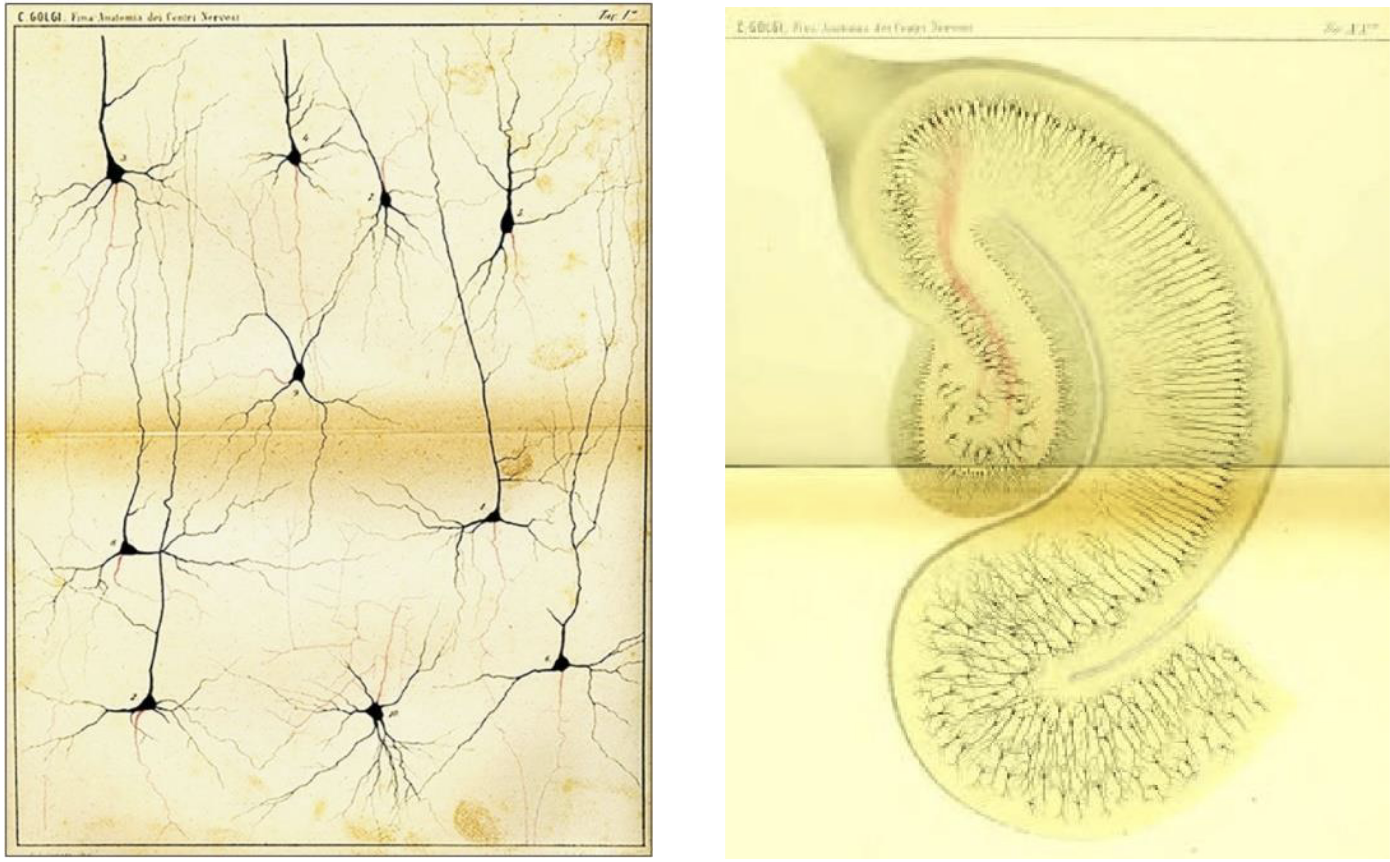高尔基染色和海马体

1958年，Frank Rosenblatt（弗兰克·罗森布拉特）根据仿生学原理，提出了感知机（Perceptron），这是最早的神经网格模型之一，感知机能够通过学习线性分类器来解决二分类问题。Rosenblatt的感知机是个天才的发明，因为当时的计算技术还没有数字化，Rosenblatt训练感知机的过程，都是靠手动切换开关完成的。尽管很原始，但通过训练，感知机最终获得了形状识别的可靠能力。

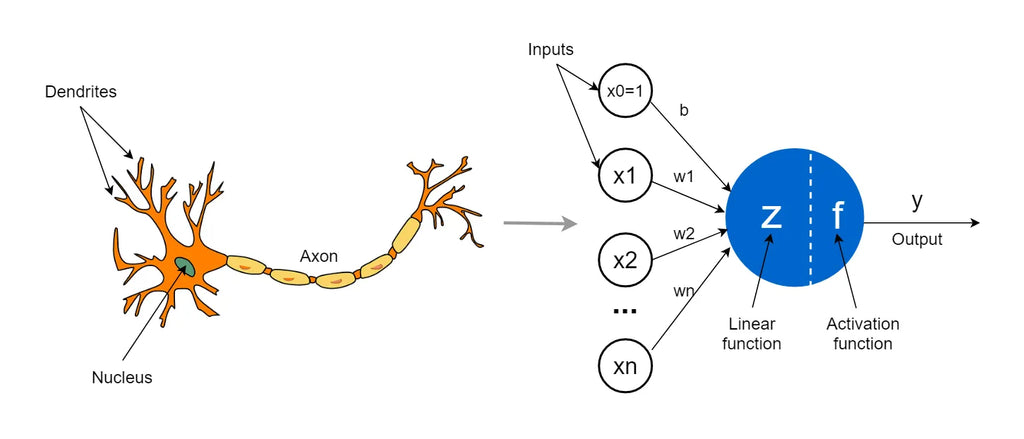感知机示意图

感知机一度被誉为重大的技术进步。但这一发明过于超前，世界还未为它的诞生做好准备 -- 直到50年以后，人们才明白，神经网络需要数字化输入输出设备、大量的算力和存储，而最终还需要海量的数据。毕竟，人脑有超过1000亿个神经元组成，在1958年，人类只能模拟大脑容量的几亿分之一。

因此，感知机带来的热浪仅持续不到一年，就受到猛烈的攻击。其中最大的反对者，正是达特矛斯AI研讨会的发起人之一马文.明斯基，和另一位数学家、计算机科学的先驱 -- 西摩.佩珀特。他们在1969年出版了一本名为《感知机》的书，抨击感知机缺乏严谨的理论基础 -- 实际上直到今天，人工智能仍然不能为自己找到坚实的数学基石，在很多时候，它的行为仍然是一个黑盒子 -- 这一点倒是很像大脑。

感知机是基于数据的机器学习模型。在感知机遭到重创之后，机器学习阵线不得不沉寂十多年之久。而在此期间，知识工程与专家系统则占据了风头。其中最有名的，可能是一个名为内科医生-I的程序，它的数据库中包含了500种疾病描述和3000种疾病表现。但是，由于现实世界太复杂，基于规则的模型能够很好地处理检索，但在推理上就显得呆板而肤浅，并且规则越多，就越难相容，于是很快也败下阵来。

专家系统是当年人类实现人工智能最后的希望。因此，专家系统的落败，也导致人工智能的发展陷入低谷，进入了冰冻的寒武纪。然而，正如地球经历寒武纪一样，在封冻的冰层之下，进化正在加速，一些革命性的突破，即将到来。

Geoffrey Hinton 2024年诺贝尔物理学奖

1986年，杰弗里·辛顿[^hinton]（Geoffrey Hinton）、大卫·鲁梅尔哈特（David Rumelhart）和罗恩·威廉姆斯（Ron Williams）发表了反向传播算法。这是深度学习的奠基之作，它使得多层神经网络的训练成为可能，从理论上，我们向模拟有1000亿神经元的大脑迈出了至关重要的一步。但深度学习的时代并没有立刻到来，人工智能还被封印在厚厚的冰雪之下。

又过去了10多年。1998年，Yann LeCun(杨立昆)提出了LeNet，这是最早的卷积神经网络，也是人类历史上第一个有实际用途的神经网络。它被广泛应用于全美的自动提款机上，用来读取支票上的数字。Yann LeCun的成功再次掀起了人工智能浪潮，也最终把机器学习路线重新带回到人们的视野中来。

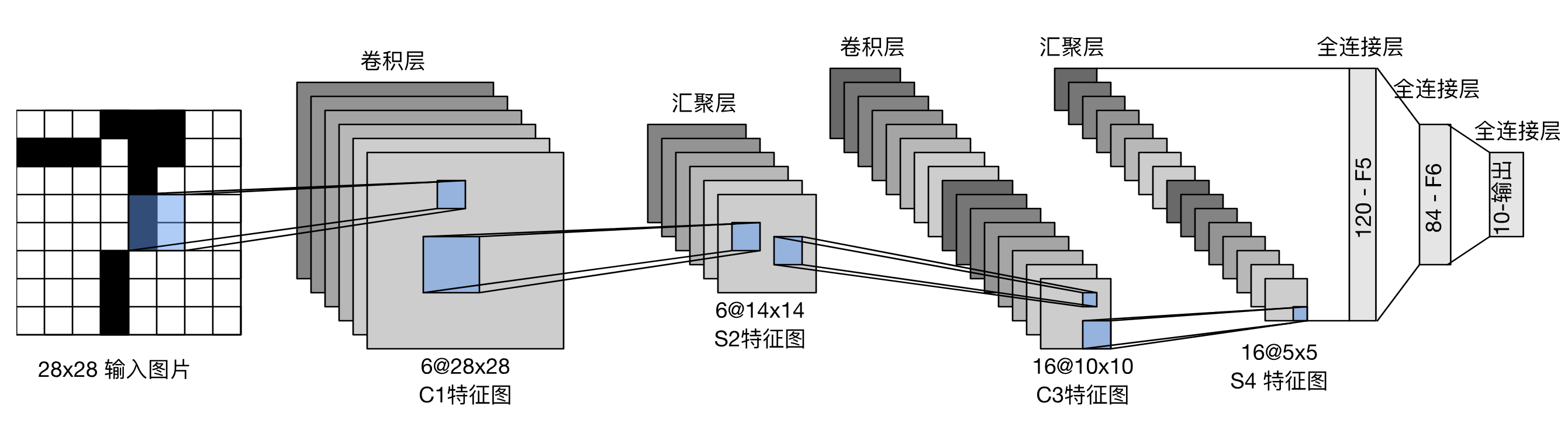LeNet, by Yann LeCun

不过，Yann LeCun的成功还无法产生势如破竹、摧枯拉朽般的攻势。相反地，在短暂的热闹之后，人工智能的研究似乎再次进入休眠期。不过，这一次它只是小憩了4年，很快，它将被AlexNet唤醒，随后便如河出伏流，一泄千里。

而在这次复苏的背后，两位华人科学家--黄仁勋和李飞飞则是最重要的幕后英雄。前者以英伟达的显卡和Cuda引擎为深度学习提供了强大的算力，后者则以ImageNet数据集，为卷积神经网络提供了土壤和营养。

Info

李飞飞
尽管李飞飞荣获了美国工程院院士、医学科学院院士和艺术与科学学院院士，但世界可能仍然大大低估了她的主要贡献 -- ImageNet的重要性。如果没有第谷长达20余年的天文观测，就不会有开普勒三大定律，也就不会有牛顿第三定律。牛顿曾说自己是站在了巨人的肩膀上，他所说的巨人当然不是莱布尼茨，而是第谷和开普勒。
李飞飞正是当代的第谷。

AlexNet也是一个卷积神经网络，它由Alex Krizhevsky, Ilya Sutskever和Geoffrey Hinton提出，在2012年的ImageNet竞赛中，取得了85%的识别准确率，比上一届的冠军整整提升了10%！LeNet只能运用在一个很小的场景下，处理很小规模的数据集，而AlexNet则是在超过1000个分类的图片上进行的识别，它的成功显然更具现实意义和突破性。AlexNet让基于数据驱动的机器学习路线加冕成为王者。直到今天，尽管机器学习还存在种种不足，我们离通用人工智能还不知道有多长的距离，但是，似乎再也没有声音质疑机器学习，而要改用基于规则的专家系统了。

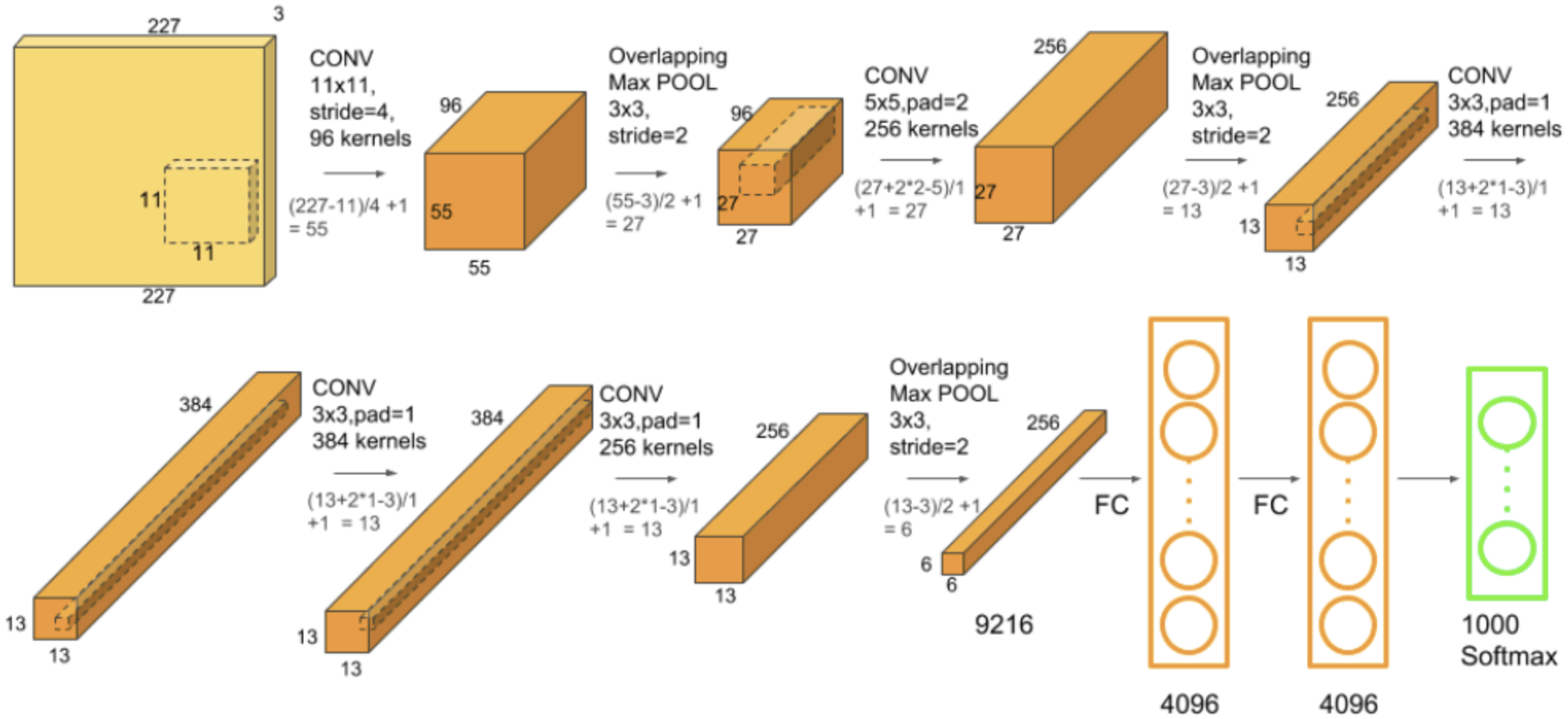AlexNet

下一个突破则是机器视觉对人类的超越。根据研究，在ImageNet数据集上人类的分类能力极限是5.1%的错误率。一旦机器视觉的错误率低于这个指标，也就战胜了人类，意味着人工智能在视觉上的应用完全成熟。

这个决定性的胜利是由华人科学家何明恺在2016年取得的。他通过深度残差网络，将神经网络的层数增加到了惊人的（与当时的水平相比）152层，但通过巧妙的设计，允许输入数据在训练阶段绕过其中的某些层，从而部分解决了深层网络中的梯度消失问题。

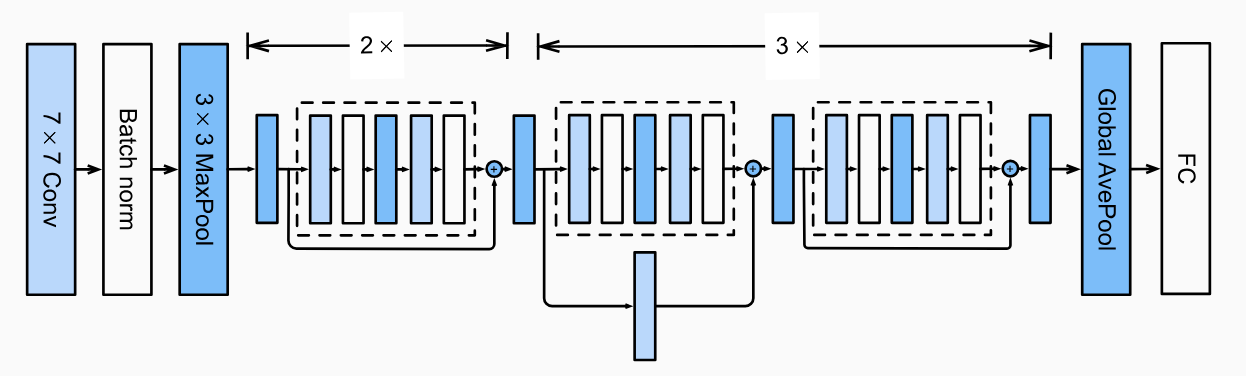ResNet-18

最终，resnet在识别错误率降到了4.5%，显著地超越了人类的极限！再也没有任何理由怀疑和拒绝人工智能的应用了！

到此为止，机器学习路线取得了压倒性的胜利，人工智能研究就进入加速时代。在短短的几年后，甚至自然语言理解也被突破，以transformer为代表的架构在自然语言理解、文生图、文生视频、编程等多个领域都取得了成功。

行百里者半九十。人类的终极愿景 -- 通用人工智能（AGI）何时能产生还未可知。人工智能在未来应该成为人类的伴侣，但此刻，人类的亚当还没能造出自己的夏娃。此外，尽管当代人工智能模型已经极为强大，但它内部的运行机制仍然没有坚实的理论基础，AI引起的伦理问题才刚刚暴露，这些都是未来有待我们攻克的一道道关卡。

  • 需要 4 分钟阅读时间

在这一刻抄底，胜率高达95%

在4月8日，我们发表了一篇名为《1赔10，3月27日我抄底了》的文章，基于坚实的统计数据，说明了为什么当天应该抄底。时间过去了半年，中证1000又为我们提供了两个新的例证。这篇文章我们就来回顾一下。

原理和定义

我们先介绍一下原理。你可能观察到，当发生一段连续下跌时，那么下跌的幅度越大，则反弹的力度就越大，并且越可能发生反弹。这就像弹簧一样，或者像是蹦极 -- 在连续下跌到某个点之后，总会往回弹一点。

但我们需要求出连续下跌到什么程度时，反弹的概率会是多大。这样一来，我们的操作才有更有底气和依据。

首先需要定义什么是连续下跌。实际上，我们可以像前文所述，使用每日涨跌。但在这篇文章里，我们想尝试另一种方法，即通过连续阴线区间的跌幅来定义，这样可以过滤一些假信号。

具体的计算方法如下图：

我们先看图中序号1到序号2这一段。这是10月8号到10月11日的走势。10月8日这一天跳空高开，接着一路下跌直到10月11日，8号开盘买入的人，到11日收盘时，亏损达到15.8%。这个损失，就是我们所说的连续阴线区间的跌幅。

我们再看序号3到序号4这一段。这是11月14日到11月18日的情况，14日开盘买入者共亏损7.5%，连续阴线区间的跌幅就是7.5%。

如果我们使用连续下跌（而不是连续阴线的区间跌幅）来计算最大跌幅，将会是从11月12日起开始计算下跌，但提前一天（11月15日）就可能给出抄底信号，这个信号就有点过早。因为在这区间中，出现了一天的假阳线（13日，下跌但收阳线）。这一天筹码发生交换，假设前一日亏损者把筹码全部倒给了新入场者，那么活跃交易者的持仓成本是下降的，他们还能再扛一阵子。

这是我们这次改进中，使用连续阴线的区间跌幅的原因。但实际上两种定义各有优劣，你可以使用机器学习模型来决定何时使用哪一个。

代码实现

既然模型定义清楚，现在我们就开始实现。这段代码需要用到发现连续阴阳线的一个函数，我们把它定义为find_runs:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def find_runs(x):
    """Find runs of consecutive items in an array.
    """

    # ensure array
    x = np.asanyarray(x)
    if x.ndim != 1:
        raise ValueError("only 1D array supported")
    n = x.shape[0]

    # handle empty array
    if n == 0:
        return np.array([]), np.array([]), np.array([])

    else:
        # find run starts
        loc_run_start = np.empty(n, dtype=bool)
        loc_run_start[0] = True
        np.not_equal(x[:-1], x[1:], out=loc_run_start[1:])
        run_starts = np.nonzero(loc_run_start)[0]

        # find run values
        run_values = x[loc_run_start]

        # find run lengths
        run_lengths = np.diff(np.append(run_starts, n))

        return run_values, run_starts, run_lengths

为了让大家都能复现代码，我们使用了akshare来提供数据。这是一个免费、开源的行情数据源。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import akshare as ak
now = datetime.datetime.now().date()
start = now - datetime.timedelta(days=365*4)

start_date = start.strftime("%Y%m%d")
end_date = now.strftime("%Y%m%d")

# 通过akshare获取中证1000日线数据（近1000天）
bars = ak.index_zh_a_hist(symbol="000852", start_date=start_date, end_date=end_date)

bars.rename(columns = {
    "日期": "date",
    "开盘": "open",
    "最高": "high",
    "最低": "low",
    "收盘": "close",
    "成交量":"volume"
}, inplace=True)

bars["date"] = pd.to_datetime(bars["date"])
bars.set_index("date", inplace=True)

bars["flag"] = np.select([bars["close"] > bars["open"], 
                          bars["close"] < bars["open"]], 
                          [1, -1], 
                          0)
v, s, l = find_runs(bars["flag"] == -1)

cum_neg_returns = []
for vi, si, li in zip(v, s, l):
    if vi and li > 1:
        cum_neg_returns.append((bars.index[si], 
                                bars.index[si + li-1], 
                                bars.close[si + li -1 ]/bars.open[si] - 1))

r = pd.DataFrame(cum_neg_returns, columns=["start", "end", "cnr"])
r.cnr.hist()

从生成的直方图来看，连续跌幅达到7.5%以后的次数就很少了，也就是，连续下跌超过7.5%，还能继续下跌是小概率事件。

我们看一下连续下跌最厉害的10次，分别是什么情况：

1
r.nsmallest(10, "cnr").sort_values("end", ascending=False)
start end cnr
107 2024-11-14 2024-11-18 -0.075433
106 2024-10-08 2024-10-11 -0.158511
89 2024-03-21 2024-03-27 -0.071948
88 2024-01-26 2024-02-05 -0.190592
87 2024-01-19 2024-01-22 -0.067846
78 2023-10-16 2023-10-23 -0.074109
45 2022-09-15 2022-09-19 -0.066983
37 2022-04-20 2022-04-26 -0.170335
34 2022-03-14 2022-03-15 -0.066983
33 2022-03-03 2022-03-09 -0.086669

我们看到2024年就发生了5次，分别是1月22日、2月5日、3月27日、10月11日和最近的11月18日。其中2月5日和10月11日这两次下跌幅度很大，后面的反弹也就很大，果然是风浪越大鱼越贵！

1月22日这次能出现在表中非常意外，毕竟这一次只下跌了两天。但是，随后也确实出现了一波持续3天的小反弹，涨幅超过6.1%，还比较可观。

底该怎么抄？

在11月8日收盘时，阴线连续下跌幅度为7.54%，盘中跌幅更大，所以，在盘中就出现了连续跌幅达到7.54%的情况。如果此时你决定抄底，成功的概率有多大？

有一个奇怪的pandas函数可以帮我们计算出来：

1
2
decline_ratio = -0.075433
r.cnr.le(decline_ratio).mean()

它的奇妙之处在于，le用来找出小于等于decline_ratio的数据，把它们标记为true,其它的标记为false,然后mean用在bool变量上，会求出真值的比例，也就是我们要找的概率！

这个概率是4.63%。如果你在此时抄底，那么还有4.63%的概率，你需要忍受继续下跌，这就是发生在10月9日的情况。按照概率的提示，你大概会在10月9日的盘中杀进来，然后要忍受此后两天的继续下跌，这个跌幅跟你之前看到的差不多（也是7.5%左右）。

不过，好消息是，如果你在10月9日杀进来，你有在10月10日选择小幅盈利出局的权利。如果你在这一天选择出局，把筹码倒给了新入场的人，他们还可以再抗7.5%的跌幅！这就是为什么股谚说多头不死，下跌不止。

如果你不会编程，可以通过下面的表格速查抄底成功概率：

1
2
3
4
5
6
data = []
for loss in np.linspace(-0.06, -0.076, 15):
    data.append((loss, 1- r.cnr.le(loss).mean()))

df = pd.DataFrame(data, columns=['最大亏损', '抄底胜率'])
df.style.format("{:.1%}")
  最大亏损 抄底胜率
0 -6.0% 87.0%
1 -6.1% 87.0%
2 -6.2% 87.0%
3 -6.3% 87.0%
4 -6.5% 88.0%
5 -6.6% 89.8%
6 -6.7% 90.7%
7 -6.8% 93.5%
8 -6.9% 93.5%
9 -7.0% 93.5%
10 -7.1% 93.5%
11 -7.3% 94.4%
12 -7.4% 94.4%
13 -7.5% 95.4%
14 -7.6% 96.3%

再往后胜率不变（因为数据量少），所以就没有列出了。在实际操作中，可以从-6%之后开始，使用马丁格尔交易法。

Tip

我在这里没有使用最高价和最低价。这两个价格的稳定性不如收盘价与开盘价（即成交量少）。但你也可以试试。

你还可以计算出抄底之后的可能获利。你可以这样定义：从连续下跌之后出现的连续阳线涨幅，即为抄底之后的盈利。这个计算比较简单，你可以先过滤出连续跌幅大的，再通过循环来计算此后的平均收益。

百闻不如一练。我讨厌读那些看上去很美好，但无法验证的文章。很多时候，读这些文章只是在浪费时间，因为你都不知道哪句是真的，反正都无法验证。

同往常一样，这篇文章同样提供可运行的代码。你只要登录Quantide Research平台，就可以运行本文的代码验证我们作出的结论，然后选择下载本文代码，持续跟踪连续下跌引起的反弹信号。

加入星球，就可以拿到门票。在星球（及Quantide Research平台）里，我们已经发布了可alpha101因子库（可运行）、5个年化超过15%的因子，还有三角形整理检测等代码。未来将继续以更新公众号的频率，持续同步发布笔记相关代码。

如果你不明白这里概率计算的原理，或者想为自己打下坚实的量化基础，可以考虑选修《量化24课》或者《因子分析与机器学习策略》。

  • 需要 3 分钟阅读时间

捕捉主力-最大成交量因子

因为黑夜，更能看见满天星光 | ©️ Nathan Jennings

今天跟一位朋友聊天，他想换到量化行业，有点担心是否有点为时已晚，又或者大环境不好。于是我用这句话鼓励他：

因为黑夜，更能看见满天星光。

低谷之中，必有转机，熬过黑暗，前方自有光明。

其实在我身边，已经有好几位『普通人』成功地转向了量化。我之前有一位策略研究员，前几天跟我通了个电话，告诉我已经有私募接洽他，希望买他的策略。他已经注册了自己的公司。他是一个真正的传奇，我会在恰当的时候，讲述他的故事，带给更多人启迪。

做你热爱的事情，不用管其它人给现在的你打上的标签，不要被他人定义。

You gotta be brave。

只要你还愿意追逐梦想，你就不是平庸的。

言归正转。

在第十二课，我承诺给大家讲如何发现新的因子。这活儿光说不练不行，我得真真正正拿出一个还没有广泛传播的因子（策略）出来。今天就来兑现这个承诺。我们探索因子，无非就是量价时空四大维度。这里面关于成交量的因子最少，所以，今天就介绍一个我自己探索的因子。

如有雷同，纯属巧合（读书太少）。这个因子是基于成交量，运用羊群效应的原理构建的。

因子还没被挖完吗？

在说书之前，先回答一个问题。因子难道还没有被挖掘完吗？毕竟，全世界有这么多做量化的人。

事实是，这世界算力不够，所以，还存在大量的关系没有发掘出来。小市值因子之父，Rolf Banz探索小市值因子的故事，也许能很好说明这一点。

1980年前后，Rolf Banz发表了一篇论文《The relationship between return and market value of common stocks》，向世界介绍了小市值因子。

Banz 的这篇论文并不复杂，只有 16 页纸。论文中并没有使用高深的数学，只是使用了基础的统计科学，GLS 和 OLS。如果当时有计算机可用的话，这个推导过程会显得格外简单。

甚至，我们可以仅凭他论文中的这张图来理解小市值因子：

收益与市值分导关系

在这张图中，Banz把资产按市值大小分成了5组，第一组是市值最小的一组，第5组是市值最大的一组。很显然，其它几组的收益都与市值大小有着线性关系，但第一组，即小市值组有更大的月度收益，不能被线性回归。

就是这样简单的一个事实，帮助Banz获得了小市值之父的称号。如果说威廉.夏普发现了第一个因子的话，Banz就是发现第二个因子的人。

Banz 用到的数据来自 1926 年到 1975 年。这些数据就在芝大的 CRSP 数据库里。在漫长的 50 多年时间里，一直在静静地等待有人发现她的价值。芝大经济学人才辈出，期间不知道有多少人接触过这份数据。如此低垂和芳香的果实最终却被 Banz 采摘。

我想，这足以说明，在任何时代，在任何圈子，都会有一些低垂的果实，等待有心人去采摘。

但是，更加惊人的是，另一颗低垂的果实，就出现在Banz自己的论文里。在上图中，资产实际上是被分成了25组。在按市值划分的每个组内，Banz又按波动率将资产分成了5组（在图上纵向分布）。第一组是波动率最大的一组，第5组则是波动率最小的一组。

很显然，在每一个组合中，低波动率的资产收益都大于高波动率的资产。

实际上，这里出现了另外一个因子，就是低波动因子。我们回测过，日线低波动因子可以达到16.4%的年化Alpha。月线可以达到6.3%左右的年化，因子IC是0.04，相当可观。

然后，直到10年之后，Haugen和Baker才发现和命名了低波动因子。Banz做完了几乎所有工作，但却与这项发明失之交臂。

低垂的果实永远都会有的

最大成交量因子

这个因子也可以叫做主力因子。它的构造原理是，价格的方向是由资金里的主力决定的。因为当个体处于群体中时，其行为和决策受到群体影响，往往会失去理性，变得更加情绪化和冲动。个体往往会受到他人引导，最终会跟随头羊的方向前进，这就是羊群效应。

主力才能决定方向，决定方向的力量也就是主力。因此，主力方向是可以建模的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import pandas as pd

def max_volume_direction(df, win=40):
    old_index = df.index.copy()
    df = df.reset_index().set_index(np.arange(len(df)))
    df["flag"] = np.select([
        df["close"] > df["open"],
        df["close"] < df["open"]
    ], [1, -1], 0)

    df["move_vol_avg"] = df["volume"].rolling(window=win, min_periods=win).mean().shift(1)
    df["argmax"] = df['volume'].rolling(win, min_periods=win).apply(lambda x: x.idxmax())
    df.fillna(0, inplace=True)
    df["move_vol_max"] = df.apply(lambda row: df.loc[row['argmax'], 'volume'], axis=1)
    df['vr'] = df['volume'] / df['move_vol_avg'] * df["flag"]
    df["span"] = df.index - df["argmax"]

    def calc_rolling_net_balance(df):
        pos = df["argmax"].iloc[-1] + 1
        sub = df.loc[pos:,]
        return (sub["flag"] * sub["volume"]).sum() / df["move_vol_max"].iloc[-1]

    balances = []
    for sub in df.rolling(win):
        b = calc_rolling_net_balance(sub)
        balances.append(b)

    df["move_balance"] = balances

    return df[["vr", "move_balance", "span"]].set_index(old_index)

这段代码的逻辑是，如果某个bar的成交量相对于过去一段时间的平均成交量异常放大（用该bar的成交量除以平均成交量，记为vr），那么它就可能是主力的操作。我们认为，该根bar的方向，有较大概率是此后主力的运作方向。

如果这根bar是阳线，它反应的是买入操作；如果这根bar是阴线，它反应的是卖出操作（记为flag）。

主力为了测试对手盘和跟风盘，在试盘之后，有可能中断操作一段时间，借此观察盘面变化。因此，我们要考察该bar之后一段时间的交易情况，把这部分成交量换算成净余成交量（记为move_balance），再除以主力操作的那个bar的成交量（『归一化』）。如果净余成交量与主力bar是同向的，说明对手盘很小（或者没有成为对手的意愿）；如果净余成交量与主力bar相反且较大，则主力的意图有可能难以实现，主力可能暂时放弃操作。

我们拿一个样本测试一下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import akshare as ak
def test(bars, thresh=5):
    bars.index = np.arange(len(bars))
    df = max_volume_direction(bars, 40)

    bars.rename(columns={"day": "date"}, inplace=True)
    cs = Candlestick(bars, height=750)
    # add up markers
    df["close"] = bars["close"]
    x = df[np.isfinite(df.vr) & (df.vr > thresh)].index
    y = df[np.isfinite(df.vr) & (df.vr > thresh)]["close"] * 1.05
    cs.add_marks(x, y, name="up", marker="triangle-up")

    # add down markers
    x = df[np.isfinite(df.vr) & (df.vr < -thresh)].index
    y = df[np.isfinite(df.vr) & (df.vr < -thresh)]["close"] * 0.95
    cs.add_marks(x, y, name="down", marker="triangle-down", color="green")

    cs.plot()

code = "sz002466"
bars = ak.stock_zh_a_minute(symbol=code, period="30", adjust="qfq")
bars = bars[-150:].copy()

bars["volume"] = bars.volume.astype(int)

test(bars)

Attention

由于akshare无法按时间段获取30分钟线，并且只能获取固定长度的30分钟线（更早的会丢弃）k线，所以，这段代码运行的结果将会与下图不同。

在测试中，我们设置vr的阈值为5。在一些比较激进的个股上，设置为8以上可能效果会更好。

在示例中，我们看到三个向上箭头。其中前两个出现后，随后股价下跌，但反向成交量很小，表明没有对手抛盘。于是主力随后又进行了拉升。第三个箭头出现后，此后出现了比较明显的抛压信号（墓碑线），随后股价下跌。

当然，我们还需要对其进行大规模的测试。这些正是《因子分析与机器学习策略》要介绍的内容。在因子创新上，我们从量、价、时、空四个维度，都给出了创新的思路和方向，保持关注，持续为你更新！

  • 需要 5 分钟阅读时间

当交易员用上火箭科学！波和导数检测出艾略特浪、双顶及及因子构建

这篇文章的部分思想来自于 John Ehlers。他曾是雷神的工程师，当年是为NASA造火箭的。他有深厚的数字信号处理（DSP）技术背景，为石油钻探发明了最大熵频谱分析（MESA）。这种分析方法能为短暂的地震回波提供高分辩率的显示。

随后，他把这种方法应用到金融领域，并开创了名为MESA的软件公司，为交易者提供相关分析软件和教育服务。

他和JM Hurst是在证券的周期分析上贡献最大的几人之一。John Ehlers还发表了许多专著，包括《交易者的火箭科学》等。

不过，直到1989年Python才被发明，直到千禧年左右才广为人知，所以，John Ehlers的许多思想，是使用一种所谓的Easy Language表达的。我们尝试使用Python来传达他的一些思想，并加入了自己的理解与拓展。最后，我们将介绍基于这种思想，发现的一个因子。

毫无疑问，证券价格是一种变形的周期信号。它的基本走势由公司的价值决定，叠加交易产生的波动。

加速成长的公司，比如，正在浪头上的科技股，它们的价值曲线可能是指数函数，比如90年代的思科、2000年前后的微软，后来的苹果和现在的英伟达。基础服务类的公司，它们的价值曲线应该是参照GDP增长的直线。

Info

说到苹果，最近发布的 Mac Mini 4是相当不错。正在抢购中。几年前入手的 Macbook M1压缩mp4视频能达到6：1的加速比，Mac Mini 4估计加速比能到30:1甚至更高了，也就是1小时的影片，应该不到2分钟完成编码压缩完成。

波动则由不同风格、不同资金管理周期（其倒数即为频率）的投资者驱动。这两类曲线合成了最终的走势，并且重大事件将改变周期规律。

下面这个函数将生成一个震荡向上的价格序列。它由一条向上的直线和一个sine曲线合成。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def gen_wave_price(size, waves, slope, amp = 0.3, phase=0):
    time = np.arange(size)
    amp_factor = time * amp
    freq = 2 * np.pi * waves / size

    y = amp_factor * np.sin(freq * time + phase) + time * slope
    return y

y = gen_wave_price(100, 3, 0.5, 0.25)
plt.plot(np.arange(100), y)

这将生成以下图形：

图1. 震荡向上走势

实际上，我们已经合成了一个艾略特驱动浪：

艾略特上升5浪

合成双顶和头肩顶

关于双顶和头肩顶，我有很好的检测算法。不过，如果你对波更感兴趣的话，我可以用sine函数来捏一个。

1
2
3
4
x = np.linspace(1, 10, 100)
y = np.sin(x) + .33 * np.sin(3*x)

plt.plot(x, y)
图2 双头

头肩顶只需要再加一个sine波：

1
2
3
4
x = np.linspace(1, 10, 100)
y = np.sin(x) + .1* np.sin(3*x) + .2 * np.sin(5*x)

plt.plot(x, y)
图3 头肩顶

如果要检测股价序列中，是否存在双头，我们可以使用scipy中的curve_fit函数。既然\(np.sin(x) + .33 * np.sin(3*x)\)能拟合出双头，那么，如果我们能从价格序列中，通过curve_fit找出类似的函数，再判断参数和估计误差，就能判断是否存在双头。

这个函数泛化后，应该表示为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from scipy.optimize import curve_fit, differential_evolution

# 待推断函数
def model(x, a, b, c, d):
    return a * np.sin(b * x) + c * np.sin(d * x)

# 目标函数
def objective(params):
    a, b, c, d = params
    y_fit = model(x, a, b, c, d)
    error = np.sum((y - y_fit) ** 2)
    return error

# 推断和绘图
def inference_and_plot(x, y):
    bounds = [(0, np.max(y)), (0, len(x)), (0, 1), (0, len(x))]
    result = differential_evolution(objective, bounds)

    initial_guess = result.x
    params, params_covariance = curve_fit(model, x, y, p0=initial_guess)

    plt.plot(x, y)
    plt.plot(x, model(x, *params), 
             label='拟合曲线', 
             color='red', 
             linewidth=2)
    return params, params_covariance


# 增加一点噪声
x = np.linspace(1, 10, 100)
y = np.sin(x) + .33* np.sin(3*x)
y += np.random.normal(0.05, 0.1, size=100)
inference_and_plot(x[60:], y[60:])
图4 双头推断

这里使用了差分进化算法来自动发现参数。

我们把蓝色部分当成是真实的股价序列，红色曲线就是通过差分进化算法推断出来的拟合曲线。

波和导数

到目前为止，我们还只进行了铺垫和前戏，只是为了说明股价序列确实具有波的特性。既然如此，我们把波的一些特性给用起来。

正弦波有一个有意思的特性，就是它的导数是一个余弦波，即：

\(\frac{d}{dt}sin(\omega t)=(\frac{1}{\omega})\times cos(\omega t)\)

求导之后，变成频率相同的余弦波，而余弦波是相位提前的正弦波。我们来验证一下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
t = np.linspace(1, 10, 100)

# 原函数
y = np.sin(t)

# 导函数
dy = np.diff(y)
dy = np.insert(dy, 0, np.nan)

fig, ax = plt.subplots(figsize=(10,5))
line1, = ax.plot(y, label="原函数")

ax2 = ax.twinx()
ax2.grid(False)
line2, = ax2.plot(dy, '-', color='orange', label="导数")

lines = [line1, line2]
labels = [line.get_label() for line in lines]
plt.legend(lines, labels, loc="upper right")
plt.show()
图5 导函数与原函数关系

蓝色的线是原来的股价，黄色的则是它的导数。从图中可以看出，求导之后，频率不变，振幅变小了，相位提前，并且黄色线的每一个波峰和波谷，后面都对应着蓝色线的波峰和波谷。这意味着什么呢？

如果原函数是一个波函数，现在，我们就能提前预测波峰和波谷了。上图清楚地显示了这一点。

几乎所有的技术指标都是落后指标，但是，导函数居然帮我们预言了波峰与波谷的到来！

Tip

不要感到震惊！其实很多量化人都已经在一种浑然不知的状态下使用这个特性了。比如，你几乎肯定用过三周期的np.diff再加np.mean。只要你用了np.diff数据，就在某种程度上使用了导数。但是，清楚地知道这一特性，我们才知道何时使用、何时放弃。

让我们把话说得再明白一点：

如果原函数是一个波函数，那么，通过寻找导函数的波峰与波谷（这是利用已经发生的数据），就能提前1/4周期知道原函数何时到波峰与波谷 -- 惟一的前提是，规律在这么短的时间里，不发生改变 -- 不会总是这样，但总有一些时间、一些品种上，规律确实会保持，而你要做的，就是运用强大算力，尽快发现它们。

我们将在《因子分析与机器学习策略》课程中，将这个特性转换成一个特征，加入到机器学习模型中，以提高其对顶和底的预测能力。课程还在进行中，现在加入，会是未来几个月中，价格最低的时候。

课程助理小姐姐在这里等你！

不过，在构建机器学习模型之前，我们可以先用这个特性构建一个因子。

点击查看源码

我使用2018年到2023年间随机抽取的2000支个股，进行了因子验证，得到以下结果：

1D 5D 10D
Ann. alpha 0.138 0.096 0.078
beta 0.036 0.064 0.058
Mean Period Wise Return Top Quantile (bps) -1.180 -1.613 -1.580
Mean Period Wise Return Bottom Quantile (bps) -15.671 -11.045 -9.155
Mean Period Wise Spread (bps) 14.491 9.531 7.650

6年间的累计年化收益图如下：

图6 累计收益图

这个收益还没有进行优化。实际上，从下面的分层收益均值图来看，是可以优化的。

图7 分层收益均值图

我们可以在因子检验之前，过滤掉第10层的因子。这样处理之后，我们得到的年化Alpha将达到20.08%，6年累计收益接近3倍。

即使是纯多策略，该因子的年化Alpha也达到了14%。

因子构建及验证代码加入星球后即可获得。

Recurring Phase of Cycle Analysis

John Ehler在这篇文章里，提出了寻找周期的方法。

图8 John Ehlers's Recurring Phase Analysis

代码使用的是Easy Languange，不过这门语言对我来说一点也不easy。我不知道它是如何实现FFT的，并且还有无处不在的魔术数字。

不过，我完成了一个类似的研究。这个研究旨在揭示fft变换之后的直流分量的意义。

点击查看源码

对图1中的时间序列进行fft变换后，去掉直流分量，再逆变换回来，将两者进行对比，我们会得到这样的一个图:

图9 去掉直流分量的对比

非常有意思。

第一点，橙色的线是去掉直流分量后的序列（的实部）。它与原序列之间的差值是一个常数，这个常数竟然是原序列的均值！

1
assert np.mean(y) == np.abs(y - y2)

这就是直流分量的真实含义。从数学上讲是一个均值，从交易上讲，它是公司的定价，一切波动都在围绕它发生。

第二点，y与y2的模的差分有上下界。当股价上涨到一定程度之后，一部分能量被浪费在虚部的方向上，该方向是与实部正交的方向，从而导致这个差分有上下界。这似乎是图8中，John Ehler要揭示的信息。

如果一个函数有上下界，它对交易的帮助就太大了。

  • 需要 4 分钟阅读时间

[1103] QuanTide Weekly

本周要闻

  • 英伟达和宣伟公司纳入道指
  • 制造业PMI时隔5个月重返景气区间
  • 三季报收官，8成上市公司实现盈利

下周看点

  • 周二：美国大选投票日（美东时间）
  • 周二：财新发布10月服务业PMI
  • 4日-8日，人常会：增量政策工具或将揭晓
  • 周六：统计局发布10月PPI/CPI

本周精选

  1. 一门三杰！一年翻十倍的男人发明了 UO 指标
  2. 世界就是一个波函数：直流分量差分因子获得15.%年化
  • 道琼斯指数发布公告，将英伟达和全球涂料供应商宣伟公司纳入道琼斯工业平均指数。英伟达将取代英特尔，宣伟将取代陶氏化学。
  • 统计局发布，10月份制造业PMI 50.1%，环比上升0.3。这是制造业PMI连续5个月运行在临界点以下后重新回到景气区间。

  • 统计数据显示，近八成上市公司前三季度实现盈利，近五成实现净利润正增长。消费品行业呈现明显修复态势，高技术制造业经营具有韧性，农林牧渔、非银金融、电子、社会服务等行业净利润增幅居前，同比增速达507%、42%、37%、30%。

  • 人大常会会11月4日至8日在北京举行，前期财政部提及的一次性新增债务额度和“不仅于此”的增量政策工具，或者将在本次会议上揭晓答案。

根据财联社、东方财富、证券时报等资讯汇编

一年十倍男发明了UO

Larry Williams，1987 年世界期货交易大赛冠军

指标 Ultimate Oscillator（终极振荡器）是由 Larry Williams 在 1976 年发表的技术分析因子。

Larry 是个牛人，不打嘴炮的那种。他发明了 William's R（即 WR）和 ultimate ocsillator 这样两个指标。著有《我如何在去年的期货交易中赢得百万美元》一书。他还是 1987 年世界期货交易大赛的冠军。在这场比赛中，他以 11.37 倍回报获得冠军。

更牛的是，在交易上，他们家可谓是一门三杰。

Michelle Williams

这是他女儿，michelle williams。她是知名女演员，出演过《断臂山》等名片，前后拿了 4 个奥斯卡最佳女配提名。更厉害的是，她在 1997 年也获得了世界期货交易大赛的冠军，同样斩获了 10 倍收益。在这个大赛的历史上，有这样收益的，总共只有三人，他们家占了俩。

这件事说明，老 williams 的一些交易技巧，历经 10 年仍然非常有效。

Larry Williams 的儿子是位心理医生，著有《交易中的心理优势》一书。近水楼台先得月，身边有两位世界冠军，确实不愁写作素材。

这是指标的计算公式。

\[ \text{True Low} = \min(\text{Low}, \text{Previous Close}) \\ \text{True High} = \max(\text{High}, \text{Previous Close}) \\ \text{BP} = \text{Close} - \text{True Low} \\ \text{True Range} = \text{True High} - \text{True Low} \\ \text{Average BP}_n = \frac{\sum_{i=1}^{n} BP_i}{\sum_{i=1}^nTR_i} \\ ULTOSC_t=\frac{4Avg_t(7) + 2Avg_t(14) + Avg_t(28)}{4+2+1} \times 100 \]

它旨在通过结合不同时间周期的买入压力来减少虚假信号，从而提供更可靠的超买和超卖信号。Ultimate Oscillator 考虑了三个不同的时间周期，通常为 7 天、14 天和 28 天，以捕捉短期、中期和长期的市场动量。

这个公式计算步骤比较多，主要有 true low, true high 和 true ange, bull power 等概念。

用这个图来解释会更清楚。

所谓的 true range，就是把前收也考虑进行，与当天的最高价、最低价一起，来求一个最大振幅。然后计算从 true low 到现价的一个涨幅，作为看涨力道（Bull Power）。

最后，用看涨力道除以真实波幅，再在一定窗口期内做平均，这样就得到了归一化的看涨力道均值。

最后，它结合长中短三个周期平均，生成最终的指标。

从构造方法来讲，它与 RSI 最重要的区别是，加入了 high 和 low 两个序列的数据。

做过交易的人知道，关键时刻最高价和最低价，都是多空博弈出来的，它是隐含了重要信息的。如果实时盯过盘口的人，可能感受更深。

像最高点，它是主力一口气向上吃掉多少筹码才拿到的这个最高点。上面的筹码吃不掉，最高价就定在这个地方。吃不掉的筹码是更大的资金的成本或者其它什么心理价位，就是未来的压力位。

因此，ultimate oscillator 与 RSI 相比，是包含了更多的信息量的。希望这部分解读，能对大家今后探索因子起到一定的启迪作用。

这个图演示了实际中的 uo 指标，看起来是什么样的。从视觉上看起来，它跟 RSI 差不多，都是在一定区间震荡的。

这个因子在回测中的表现如何？在回测中，从 2018 年到 2023 年的 6 年中，它的 alpha 年化达到了 13.7%，表现还是很优秀的。

不过因子收益主要由做空贡献。大家看这张分层收益图，收益主要由第 1 层做空时贡献。在纯多的情况下，alpha 并不高，只有 1.6%，收益主要由 beta 贡献，所以组合收益的波动比较大。

所以，这个指标在期货上会更好使。

在多空组合下，6 年的收益达到了 2.2 倍。

最后我们看一下因子密度分布图。看上去很符合正态分布，尽显对称之美。

从分层均值收益图来看，我们在交易中还可以做一点小小的优化，就是淘汰第8层之上的因子。这样调优之后，在2018年到2022年间，年化Alpha达到了24%，5年累计收益达到了2.75倍。

我们保留了2023年的数据作为带外数据供测试。在这一年的回测中，年化Alpha达到了13%，表明并没有出现过拟合。2023年的累计收益曲线如下：

同期沪指是以下跌为主。8月底开启的上涨，在时间上与DMA策略上涨巧合了。

世界就是一个波函数

从直觉上看，使用波谱分析的方法来构建因子非常自然。因为经济是有周期的，交易更是有周期的。不过在量化交易中运用波谱分析，有它的难度。

以人声的波谱分析来说，它的频率有着固定的范围，能量也有固定的范围，换句话说，它们是平稳序列。但证券价格不是。我们多次讲过这个观点，股票价格是震荡向上的随机序列，只要国家经济还在发展，因此它不是平稳的。

但我们总能找到一种方法来分析问题。

波谱变换

我们先简单地介绍波谱变换。

1
2
3
4
5
6
7
8
fft_result = np.fft.fft(close)
freqs = np.fft.fftfreq(len(close))

# 逆傅里叶变换
filtered = fft_result.copy()
filtered[20:] = 0
inverse_fft = np.fft.ifft(filtered)
inversed = pd.Series(inverse_fft.real, index=close.index)

1
2
3
4
5
# 绘制原始信号和分解后的信号
plt.figure(figsize=(14, 7))
plt.plot(close, label='Original Close')
plt.plot(inversed, label='Reconstructed from Sine Waves')
plt.legend()

第一行代码是将时间序列变换成频谱，也就是所谓的时频变换。变换后的结果是一个复数数组，其中实部是频谱，虚部是频谱的偏移。

该数组是按频率由小大到排列的，也就是数组的开始部分是低频信号，结尾部分是高频信号。元素的取值是该信号的能量。一般我们把高频信号当成时噪声。 在这个数组当中零号元素有特殊的含义，它的频率是零赫兹，也就是它是一种直流分量。

第一行是生成频率的代码。注意它只与时间序列本身的长度有关系。也就是一个序列如果长度为30个时间单位，那么我们认为它的最高频率是30次。至于该频率实际上有没有信号，要看前一个数组对应位置的数值，如果是非零，就认为该频率的波存在。

第6~第8行是对转换后的频率信号进行简单处理。我们将20号以后的数组元素置为零。这样就实现了滤波。

然后我们通过ifft将处理后的信号逆变换回来，再重建时间序列。

我们看到图像更平滑了。所以这也是一种均线平滑的方法。好，关于FFT我们就介绍到这里。

直流分量的解释

现在我们思考一个问题，将价格序列进行时频变换后，得到的直流分量，意味着什么？

这里有一个猜想，如果我们把一次振动看成一次交易 -- 买入时导致股价上升，卖出时导致股价下跌回到起点 -- 这就是一种振动，对吧？

那么，高频振动就对应着高频交易，低频振动就对应着低频交易。如果在该窗口期没有做任何交易的资金，它们就是长线资金，是信号中的直流分量。直流分量的能量越大，高频振动的能量越小，股价就越稳定。

现在，我们再进一步思考，如果在t0期直流分量的能量为e0，在t1期的能量变为e1，那么，两者的差值意味着什么？

这就意味着有新的长线资金（超过窗口期）进来了。那么，股价就应该看涨。

直流分量差分因子

这个因子的原理是把股价当成一种波动，对它按30天为滑动窗口，进行波谱分析，提取直流分量（即频率为0的分量）的差分作为因子。

1
2
3
4
5
6
7
def calc_wave_energy(df, win):
    close = df.close / df.close[0]
    dc = close.rolling(win).apply(lambda x: np.fft.fft(x)[0])
    return-1 * dc.diff()

np.random.seed(78)
_ = alphatest(2000, start, end, calc_factor=calc_wave_energy, args=(30,), top=9)

这是年化Alpha，很意外我们就得到了17%的年化：

1D 5D 10D
Ann. alpha 0.170 0.144 0.114
beta 0.022 0.030 0.040
Mean Period Wise Return Top Quantile (bps) 2.742 2.512 2.042
Mean Period Wise Return Bottom Quantile (bps) -9.614 -8.516 -7.270
Mean Period Wise Spread (bps) 12.355 11.178 9.473

我们再来看分层收益均值图。我们从未得到过如此完美的图形。它简直就像是合成出来的。

近20年累计收益17.5倍。

在《因子分析与机器学习》课程中，我们批露了更多高效率因子，并且深入浅出地讲解了因子分析和机器学习构建量化交易策略的原理，快来一起学习吧。

  • 需要 3 分钟阅读时间

一门三杰 一年翻十倍的男人发明了 UO 指标

Larry Williams，1987 年世界期货交易大赛冠军

指标 Ultimate Oscillator（终极振荡器）是由 Larry Williams 在 1976 年发表的技术分析因子。

Larry 是个牛人，不打嘴炮的那种。他发明了 William's R（即 WR）和 ultimate ocsillator 这样两个指标。著有《我如何在去年的期货交易中赢得百万美元》一书。他还是 1987 年世界期货交易大赛的冠军。在这场比赛中，他以 11.37 倍回报获得冠军。

更牛的是，在交易上，他们家可谓是一门三杰。

这是他女儿，michelle williams。她是知名女演员，出演过《断臂山》等名片，前后拿了 4 个奥斯卡最佳女配提名。更厉害的是，她在 1997 年也获得了世界期货交易大赛的冠军，同样斩获了 10 倍收益。在这个大赛的历史上，有这样收益的，总共只有三人，他们家占了俩。

这件事说明，老 williams 的一些交易技巧，历经 10 年仍然非常有效。

Larry Williams 的儿子是位心理医生，著有《交易中的心理优势》一书。近水楼台先得月，身边有两位世界冠军，确实不愁写作素材。

这是指标的计算公式。

\[ \text{True Low} = \min(\text{Low}, \text{Previous Close}) \\ \text{True High} = \max(\text{High}, \text{Previous Close}) \\ \text{BP} = \text{Close} - \text{True Low} \\ \text{True Range} = \text{True High} - \text{True Low} \\ \text{Average BP}_n = \frac{\sum_{i=1}^{n} BP_i}{\sum_{i=1}^nTR_i} \\ ULTOSC_t=\frac{4Avg_t(7) + 2Avg_t(14) + Avg_t(28)}{4+2+1} \times 100 \]

它旨在通过结合不同时间周期的买入压力来减少虚假信号，从而提供更可靠的超买和超卖信号。Ultimate Oscillator 考虑了三个不同的时间周期，通常为 7 天、14 天和 28 天，以捕捉短期、中期和长期的市场动量。

这个公式计算步骤比较多，主要有 true low, true high 和 true ange, bull power 等概念。

用这个图来解释会更清楚。

所谓的 true range，就是把前收也考虑进行，与当天的最高价、最低价一起，来求一个最大振幅。然后计算从 true low 到现价的一个涨幅，作为看涨力道（Bull Power）。

最后，用看涨力道除以真实波幅，再在一定窗口期内做平均，这样就得到了归一化的看涨力道均值。

最后，它结合长中短三个周期平均，生成最终的指标。

从构造方法来讲，它与 RSI 最重要的区别是，加入了 high 和 low 两个序列的数据。

做过交易的人知道，关键时刻最高价和最低价，都是多空博弈出来的，它是隐含了重要信息的。如果实时盯过盘口的人，可能感受更深。

像最高点，它是主力一口气向上吃掉多少筹码才拿到的这个最高点。上面的筹码吃不掉，最高价就定在这个地方。吃不掉的筹码是更大的资金的成本或者其它什么心理价位，就是未来的压力位。

因此，ultimate oscillator 与 RSI 相比，是包含了更多的信息量的。希望这部分解读，能对大家今后探索因子起到一定的启迪作用。

这个图演示了实际中的 uo 指标，看起来是什么样的。从视觉上看起来，它跟 RSI 差不多，都是在一定区间震荡的。

这个因子在回测中的表现如何？在回测中，从 2018 年到 2023 年的 6 年中，它的 alpha 年化达到了 13.7%，表现还是很优秀的。

不过因子收益主要由做空贡献。大家看这张分层收益图，收益主要由第 1 层做空时贡献。在纯多的情况下，alpha 并不高，只有 1.6%，收益主要由 beta 贡献，所以组合收益的波动比较大。

所以，这个指标在期货上会更好使。

在多空组合下，6 年的收益达到了 2.2 倍。

最后我们看一下因子密度分布图。看上去很符合正态分布，尽显对称之美。

从分层均值收益图来看，我们在交易中还可以做一点小小的优化，就是淘汰第8层之上的因子。这样调优之后，在2018年到2022年间，年化Alpha达到了24%，5年累计收益达到了2.75倍。

我们保留了2023年的数据作为带外数据供测试。在这一年的回测中，年化Alpha达到了13%，表明并没有出现过拟合。2023年的累计收益曲线如下：

同期沪指是以下跌为主。8月底开启的上涨，在时间上与DMA策略上涨巧合了。

完整测试代码加入星球后即可获取。

  • 需要 3 分钟阅读时间

[1027] QuanTide Weekly

本周要闻

  • 财政部：中国还将加大财政政策逆周期调节力度
  • 统计局：1-9月全国规上工业利润下降3.5%
  • 纽交所计划延长美股交易时间。

下周看点

  • 周一：医保目录现场谈判开始
  • 周四：统计局发布10月PMI
  • 美股Q3财报季下周将迎来最繁忙的一周

本周精选

  • 连载！量化人必会的 Numpy 编程(8) - 暴力美学，无洗盘，不拉升。洗盘模式如何检测？(应用案例5)
  • 10月25日，世行举行发展委员会第110次会议。财政部副部长廖岷表示，中国还将加大财政政策逆周期调节力度，在化解地方政府债务、稳定房地产市场、提高重点群体收入、保障民生、推动设备更新和消费品以旧换新等方面实施一系列强有力措施。中国有信心实现5%增长目录（财政部网站）
  • 1—9月份，全国规模以上工业企业实现利润总额52281.6亿元 同比下降3.5%。
  • 今日2024年医保目录现场谈判/竞价正式拉开帷幕，医保局工作人员现场点名华润医药、百特药业、康缘药业、康哲药业、宜昌人福、正大天晴等在内十余家多家企业先后进场，节奏明显快于去年。
  • 北交所分别举办券商、上市公司两场专项座谈会，会议提出，北交所将推动提高企业运用并购重组工具的能力，促进提高北交所上市公司质量和投资价值
  • 三季度中央汇金大举增持多只宽基ETF 仅4只沪深300ETF和华夏上证50ETF就耗资3000亿元
  • 纽交所计划延长美股交易时间至每个工作日22小时。

来源：财联社网站

暴力美学!无洗盘，不拉升。洗盘模式如何检测？

无洗盘，不拉升。 筹码收集阶段，股价呈现出上涨形态，也吸引到许多不坚定的跟风盘，它们将成为主升过程中的不利因素。

因此，在拉升之前，主力会采用洗盘的方式，将这些不坚定的低价筹码洗下车。这个过程中往往暴涨暴跌，犹如一匹烈马，要摆脱它身上的骑手一样。

暴力洗盘，某种程度上就成为了行情快速上涨之前的信号之一。

这篇文章，我们量化实现的技术问题：如何快速检测出洗盘模式？

L50

暴力洗盘是在证券市场上观察到的一种经验模式，因此没有严格的定义。一般把两阳夹一阴、且涨跌幅都巨大的情况认为是暴力洗盘。

在本文中我们把两阳夹两阴、且涨跌幅都较大的情况定义为暴力洗盘。

但我们介绍的方法，也完全适用于其它模式，只需要微调参数即可。

如左图所示，标的在1号位置之前，经过一段时间的吸筹，由于期间股价上涨，已经吸引了一些跟风盘。主力在1号位置拉出20cm，在这一过程中，较多跟风筹码被锁定在涨停位置。

第2天起主力开始洗盘，连续两天，分别下跌14.4%和18.9%。此时在1号位置买入的筹码因为忍受不住巨大的跌幅，忍痛交出筹码。主力筹码增加，成本降低，为后面的拉升留出了空间。

第4天主力将个股拉涨9.4%，表明洗盘结束。

随后几天的整理，主要是留出时间，让下一波的跟风盘有时间发现这支标的，并且有信心跟随买入。紧接着使用一系列小阳线做出上升趋势，最终再拉出一个20cm，从第4天起，短期涨幅高达87%。

我们为什么要使用两阳夹两阴的4天模式来定义洗盘？

因为经过两天的洗盘，从时间和空间上看，洗盘效果会更好（考虑到交易者心理因素，一些人第一天亏损后，往往还不会绝望，第二天继续下跌，更容易崩溃卖出）。另外，从一些技术指标上来看，经过连续两天大幅下跌，技术指标修复比较到位，也更能为后面的拉升腾出上涨空间。

我们为涨跌幅设置一个阈值，如果期间的每个bar的涨跌幅超过这个阈值，我们就认为发生了洗盘。在我们的示例中，使用的阈值是0.05，即涨跌5%。

下面我们来看代码实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
# 示例1
def feature_washout(bars, threshold=0.05):
    """返回在bars中最后一次洗盘结束的位置，-1表示最后一个bar,
        0表示不存在洗盘模式
    """
    close = bars["close"]
    opn = bars["open"]
    truerange = np.maximum(np.abs(close[1:] - close[:-1]), 
                           np.abs(opn-close)[1:]) 
    # 百分比化
    tr = truerange / close[:-1]
    sign = (opn < close)[1:] * 2 - 1
    signed_tr = tr * sign

这里我们使用了truerange这个变量名,是因为这段代码脱胎于技术指标TR。

这段代码解决如何将涨跌幅转换为由1,-1和0表示的模式，以便我们后面进行模式检索。

如果当天涨跌超过5%，或者实体的振幅超过5%，我们就将其标记为1或者-1，否则标记为0。标记的符号由它的形态是阴线还是阳线决定。阴线为-1，阳线为1.

我们通过这样一段简单的代码就实现了求阴阳线的功能：

1
(opn < close) * 2 -1

其结果将生成由1和-1组成的数组。无论是涨还是跌，我们总是认为，阴线是洗盘。所以，高开大阴线，即使收盘是上涨的，我们也当成洗盘来处理。

下图就是高开大阴线洗盘一例：

75%

在判断每个bar的涨跌幅、或者实体的振幅是否超过阈值时，我们使用了一个简单的技巧，即通过np.maximimum来从多个数组中，以 element-wise 的形式选取最大值。即，如果有数组\(A\)和\(B\)，那么\(np.maximum(A, B)\)将返回一个数组，其元素为\(A\)和\(B\)对应位置的元素中的较大值。

也就是，如果结果是\(C\)，那么\(C_0\)将是\(A_0\)和\(B_0\)中的较大值，\(C_1\)将是\(A_1\)和\(B_1\)中的较大值，以此类推。

除了使用\(np.maximimum\)这种 ufunc 之外，实际上\(np.max\)也可以用来完成这项任务，只是我们需要先将数组\(A\)和\(B\)堆叠成一个矩阵：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
# 示例2
A = np.arange(4)
B = np.arange(3, 7)
C = np.arange(8, 4, -1)

Z = np.vstack((A,B,C))

# 通过np.max求每列最大值
r1 = np.max(Z, axis=0)

# 通过np.maximum求最大值
r2 = np.maximum.reduce([A, B, C])

# 比较两种方法的结果是否相同
np.array_equal(r1, r2)

为了提供更多信息，示例中我们演示了三个数组按元素求最大值的情况。答案是要使用reduce方法。如果只在两个数组间进行比较，则可以只使用np.maximum。

经过示例1处理后，我们可能得到如下所示的数组：

[ ... 0.04 -0.02 -0.06 0.04 -0.04 -0. 0.2 -0.14 -0.19 0.09 -0.03 ...]

显然，我们还应该把它二值化，转换成为[大阳,大阴,大阴,大阳]（即[1, -1, -1, 1]）这样的模式：

1
2
3
4
5
6
7
8
9
# 示例3
encoded = np.select([signed_tr > threshold, 
                    signed_tr < -threshold], 
                    [1, -1], 0)

for i in range(len(encoded) - 3, 0, -1):
    if np.array_equal([-1, -1, 1], encoded[i:i+3]):
        return i - len(encoded) + 2
return 0

我们通过select方法完成了二值化转换。接下来我们通过一个逆序的循环，通过array_equal完成了模式匹配。

在回测中，我们可能需要一次性地提取出很长一段行情中所有的洗盘模式，并对其效果进行检验。上面的代码还可以通过numpy.lib.stride_tricks.sliding_window_view进行优化：

1
2
3
4
5
6
7
8
def feature_washout(bars):
    ...
    washouts = []
    for i, patten in enumerate(sliding_window_view(encoded, window_shape = 4)):
        if np.array_equal(patten, [1, -1, -1, 1]):
            washouts.append(i)

    return washouts

通过将涨跌幅二值化，我们就可以在随后方便地通过array_equal来匹配模式。我们这样做，是因为在这里定性分析基本就够了，只要涨跌幅超过5%，那么无论是跌了5.1%还是7.2%，我们都认为是洗盘。

但是，如果你觉得定量分析仍然有意义，也可以通过求皮尔逊相关系数的方法来进行模式匹配。

  • 需要 4 分钟阅读时间

不看懂这篇文章，不要在量化中使用市盈率！

在9月16日的公众号文章（《节前迎来揪心一幕！谁来告诉我，A股现在有没有低估？》），我们发表了这样一个数据，就是A股的市盈率已经处于历史低位（10%分位）。两天之后，从9月18日起，沪指迎来一轮长达两个月的小牛市。

当沪指涨回到3452时，现在的市盈率又处在哪个位置？这是我们今天要回答的第一个问题。

不过，今天的重点是研究市盈率作为量化因子的有效性。我们将提出一个暂新的视角，分别在个股及沪指上，得出有趣的结论。

市盈率因子

市盈率在量化中一般被称为估值因子。它是价值因子的一个子类。价值因子包含了账面市值比，盈利因子（ROE），投资因子等。

市盈率的计算公式如下：

\[\text{PE} = \frac{\text{股票价格}}{\text{每股收益}}\]

一般认为，低估值的公司有可能股价上涨，高估值的公司有可能股价下跌，从而完成价格对价值的回归。

但实际上，PE作为因子，坑很多。

  1. PE值依赖每股收益这一财务指标，它的发布周期是季度，因此在两次数据发布之间，它只携带了收盘价这样的噪声信息（相对因子而言）。
  2. 一般而言，因子分析是横截面分析，即是一种同一时间点上、不同资产的相同属性放在一起比较排序的分析方法。但是，资产的PE差别主要由行业决定，而不是资产自身决定。所以，把PE当成因子来求资产的 alpha， 必须进行行业中性化。
  3. 周期性行业，往往是高PE值（甚至为负数时）是买入时机，因为往后公司盈利会好转，筹码后面才有派发的机会；低PE值时则是卖出时机，因为往后公司盈利会下降，坏消息不断，这时筹码派发就只能降价派发。

不过，眼见为实。我们还是拿它来回测一下。在回测时，我们要使用PE_TTM指标而不是PE，PE_TTM是滚动市盈利。PE是以年为单位发布的，这使得它的数据响应不够及时。PE_TTM在时间周期上，它虽然仍是以一年为单位进行计算，但是它是在 4 个季度的滑动窗口上计算和发布的，所以，更能及时反映公司的盈利变化。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
start = datetime.date(2018, 1, 1)
end = datetime.date(2023, 12, 31)
universe = get_stock_list(start, code_only=True)
barss = load_bars(start, end, tuple(universe))

pe = get_daily_basic(["pe_ttm"], start, end, universe) * -1
prices = barss.price.unstack(level="asset")

merged = get_clean_factor_and_forward_returns(pe, prices)
create_returns_tear_sheet(merged)

这里的get_daily_basic是我们封装的tushare函数，对应着tushare的daily_basic函数，但它可以一次把某个指标的数据取全。

注意第6行，我们给PE乘上了-1。如果你不明白这是为什么，也许可以考虑学习《因子分析与机器学习策略》这门课。

这是回测的年化Alpha。在我们的公众号上，曾出现过好多次年化Alpha超过15%的因子 -- 它们都是从无数次失败中选出来的 -- 实际上很多因子都跟PE一样：

PE因子的年化Alpha

分层均值收益图也表明该因子不具有与收益的良好线性关系。

碰壁之后，我们再回过头来思考为什么。

首先，PE是充满噪声的数据。它实际上在一年的时间里，在一个长达250个数据点的样本中，只有4次携带了信息。当我们使用PE作为因子时，实际上是在使用CLOSE作为因子。

降噪之后，发现周期股交易信号

所以，我们下面来给PE去噪声。去噪声的方法就是将PE除以收盘价。这样得到的实际上是每股收益的倒数。

生猪行业是一个强周期的行业。我们选其中一个看看：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
def deepinsight_fundamental(ticker: str, field, start, end, inverse = False):
    df = get_daily_basic([field, "close"], start, end, (ticker,))
    df = df.xs(ticker, level="asset")

    if inverse:
        df[field] = df["close"] / df[field]
    else:
        df[field] = df[field] / df["close"]

    df["d1"] = df[field].diff()
    df.ffill(inplace=True)
    _, ax = plt.subplots(figsize=(15, 5))
    ax.plot(df.index, df["d1"], label=f"{field}_denoise")
    ax2 = ax.twinx()
    ax2.plot(df.index, df["close"], label="close", color="r")
    ax.legend(loc=2)
    ax2.legend(loc=1)
    plt.show()

start = datetime.date(2005, 1, 1)
end = datetime.date(2014, 10,31)
deepinsight_fundamental("002714.XSHE", "pe_ttm", start, end)
某生🐖企业周期图 2005-2014

这是2005年到2014年间的结果。我们看到，大约在2014年4月前后，出现一个明显的信号，随后该资产价格上涨了60%（由于tushare数据在此处未复权，实际上涨更多）。

我们再来看2015到2022年的结果：

1
2
3
start = datetime.date(2014, 1, 1)
end = datetime.date(2022, 12, 31)
deepinsight_fundamental("002714.XSHE", "pe_ttm", start, end)
某生🐖企业周期图 2014-2022

在一连串的大于零的信号中，我们关注第一个，它是买入的起涨点；在一连串的于小零的信号中，我们也关注第一个，它是下跌起点（因为季度发布时间关系，有可能滞后一点）

在上图中，我们看到，2018年9月左右，出现比较明显的买入时机，随后上涨约4倍，直到2019三季度出现强烈的卖出信号（小于-3的那根线）。此后也随即出现下跌，下跌一直持续到2020年初。此后虽然股份有过上涨，也有过波动，但信号上以弱卖出居多。

Tip

这个方法是为强周期股准备的。不适用于弱周期股。

我们已经揭示了非常有趣的一个谜底。现在，我们来回答第一个问题，沪指上涨到3450之后，现在的市盈率是高还是低？

3450点，现在沪指高了吗？

我们总是通过数据来说话。先取沪指数据：

1
2
3
4
5
6
7
import akshare as ak

pe = ak.stock_market_pe_lg(symbol="上证")
pe.set_index("日期", inplace=True)
pe.index.name = "date"
pe.rename(columns={"平均市盈率": "pe", "指数": "price"}, inplace=True)
pe.tail(15)

表1 市盈率与指数

这样我们就得到了1999年以来沪指全部市盈率数据。我们用同样的方法来查看一下全市场的盈利能力。

1
2
3
4
a = pe.copy()
a["adj"] = a.price/a.pe
a = a[["price", "adj"]]
a.plot(secondary_y='price', figsize=(15,5))
去掉噪声后的PE与指数走势

从图中可以看出，这么多年以来，A股的盈利能力（以下称指标）一直是在上涨的。但是速度略有变化。在2004年到2012年间，上涨速度较快，最终带动了指数的回归，由跌转涨，不过在6000点的高位还是有点过度反应。2016年之后，指标走势变平缓，股价也受此因素影响，这也是万年三千点的真实来由。

从2016年初到2024年初，这一指标上涨了25%，当时是2737点，上涨25%就是3421点左右。这是大的趋势来看，它不会很精确，只是一种猜想。

最后，我们来回答3450点的沪指，现在处在2016年以来的哪个分位数上。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
start = datetime.date(2016, 1, 1)
pe2016 = pe.loc[start:]

rank = pe2016.rank().loc[:, "pe"]
percentile = rank / len(pe2016)
percentile.plot()

p30 = 0.3
p70 = 0.7

# 30和70分位
plt.axhline(y=p30, color='green', linestyle='--', label='30th Percentile')
plt.axhline(y=p70, color='red', linestyle='--', label='70th Percentile')

# 获取最后一期的PE值及其日期
last_pe = pe2016['pe'].iloc[-1]
last_date = pe2016.index[-1]

# 在图上标注最后一期的PE值
plt.annotate(f'PE/分位: {last_pe:.2f}/{percentile.iloc[-1]:.1%}', 
             xy=(last_date, percentile.iloc[-1]), 
             xytext=(last_date, percentile.iloc[-1] + 0.05), 
             arrowprops=dict(facecolor='red', shrink=0.05))

# 添加图例
plt.legend()

# 显示图形
plt.show()

数据表明，当前处在2016年以来的54%分位，现在处在进可攻、退可守的区间，没有明显的指标压制，也没有提供进攻的势能。在这个点上怎么操作，交给别的指标吧！

  • 需要 3 分钟阅读时间

拯救CCI！因子纯化后，证实CCI确实是超有效的技术指标！

CCI（商品通道指数） 由 Donald Lambert 研发，首次发表于 1980 年的《商品期货》杂志，一直以来很受交易大量推崇。但是，简单地将这个指标作为因子进行因子检验，差点使明珠蒙尘。最后，因子密度分布图揭示了真相，通过因子纯化，最终检验结果给出了与传统经验一致的结论！

CCI的计算公式是：

\[ CCI=\frac{Typical Price - MA}{.015 * Mean Deviation} \]

其中，

\[ \text{Typical Price}_t=(H_t+L_t+C_t)\div 3 \\ MA = Moving Average \\ Moving Average = (\sum_{i=1}^PTypical Price)\div P \\ Mean Deviation = (\sum_{i=1}^P|Typical Price - MA|)\div P \]

简单来说，CCI 表示了价格对移动平均线的徧离程度。

Tip

MACD, PPO, CCI 和 BIAS 是一组非常相似的指标，它们的区别主要在于选择的价格序列不同，是否进行了归一化。在本章我们不会介绍 BIAS 指标，这里就顺带提一下。它的公式是：

\[ \text{Bias} = \frac{\text{当前价格} - \text{N 日移动平均线}}{\text{N 日移动平均线}} \times 100 \]

这个对比给我们提示了创新因子的一个思路。

CCI 使用最高价、最低价和收盘价的平均值作为价格序列的想法，在很多地方都很常见。本质上，它是对 vwap 的一种近似。因此，在有 vwap 数据可用的前提下，直接使用 vwap 数据有可能更好，后者的博弈含义更明确。

CCI 公式当中有一个魔术数字：0.15. 它的作用是为了使 CCI 的值标准化到一个合理的范围，并且能在-100和100边界处有信号意义。起初，公式的设计者 lambert 认为，当 CCI 在[-100,100]区间内时，意味着价格在随机波动，是不值得交易的。而只有当 CCI 绝对值超过了 100 时，才认为有趋势出现，即当 CCI 上穿 100 时买入，下穿-100 时卖出。

我们先用一个简单的双轴图观察一下这个指标。

1
2
3
4
5
6
7
8
9
df = PAYH.copy()
df['cci'] = ta.CCI(df.high, df.low, df.close, 14)

axes = df[['close', 'cci']].plot(figsize=(14, 7), 
                            subplots=True, 
                            title=['PAYH', 'cci'])
axes[1].set_xlabel('')
sns.despine()
plt.tight_layout()

这是输出结果：

输出结果中，我在两处CCI穿越 \(\pm 100\) 的位置上标注了交易信号，以说明CCI的信号作用。这只是单个资产、某小段时间上的观察结果，说明不了问题。

现在我们运行因子检验来测试一下：

1
2
3
4
5
_ = alphatest(2000, start, end, 
              calc_factor = lambda x: ta.CCI(x.high, 
                                             x.low, 
                                             x.close, 
                                             14))

看起来因子测试的结果不是很好。

但是，只要对 CCI 的原理略加分析，我们就很容易明白，它不适合直接当成因子来使用。因为CCI的交易信号是，当CCI穿越\(\pm 100\) 时，就发出交易信号。它是一种事件信号，并不是我们通常意义上的因子。

下面，我们从因子分布的角度来讲一下为什么。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
cci = barss.groupby(level="asset")
            .apply(lambda x: ta.CCI(x.high, 
                                    x.low, 
                                    x.close, 
                                    timeperiod=14
                                    )
                )

with sns.axes_style('white'):
    sns.distplot(cci)
    sns.despine()

从密度分布图来看，因子分布出现了双峰。

我们在课程中讲过，如果因子的分布出现双峰，这个因子往往包含了多种因素，它是不纯粹的。现在，我们面临的正是这种情况。在这种情况下，进行因子分析，我们需要先对因子进行“纯化”。

1
2
3
4
5
6
7
8
cci = barss.groupby(level="asset")
            .apply(lambda x: ta.CCI(x.high, 
                                    x.low, 
                                    x.close, 
                                    timeperiod=14))
with sns.axes_style('white'):
    sns.distplot(cci[cci> 0])
    sns.despine()

输出结果如下：

现在，我们看到的 cci 的分布就是单峰的了。然后我们对它进行因子检验，看看结果如何：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def calc_cci(df, n):
    cci = ta.CCI(df.high, df.low, df.close, n)
    cci[cci < 0] = np.nan
    return cci * -1

alphatest(2000, 
         start, 
         end, 
         calc_factor= calc_cci, args=(14,), 
         max_loss=0.55, long_short=False)

注意，这段代码的第三行，我们对返回前的CCI 进行了修正，使其负值部分被置为nan，从而它们将会在因子检验中被抛弃掉。这是之前讲Alphalens框架时讲过的内容。

也正是因为丢弃了一半的因子，所以，在调用Alphalens时，我们需要将max_loss参数设置为大于0.5（具体看maxlosserror报告）。

基于纯化后的因子，回报是惊人的。它没有我们之前调谐过的RSI那么强，但是，我们是在纯多条件下得到的结果，因此它格外吸引人。

年化Alpha图

Alpha 达到了年化 19%。而且这个因子呈现比较好的正向单调性，见分层收益图：

因子分层收益均值图

不过，它在纯多的情况下，累计收益表现不是很稳定。这一点也从前面的年化收益图中的beta值可以看出来，受市场波动影响比较大。

累积收益图

但是我们不一定非要纯多，本来CCI就是期货指标。我们来看看多空组合的情况：

多空组合时的Alpha

不仅Alpha收益很强，而且beta被对冲到几乎没有！在beta为零的情况下，累积收益就应该是平稳向上、且波动很小，我们来看看是否是这样：

多空组合时的累积收益

这也许是 CCI 如此受人推崇的原因之一。

不过，这里的因子检验并不等同于实盘，因为操作手法不一样。在因子检验中，我们是按因子值进行的加权多空操作，在实盘中，会固定按CCI是否穿越\(\pm 100\)来确实是否开仓。在因子检验中，我们的开仓条件会更宽松一些，有一些自适应的味道。

本文附有代码和数据，可复现。加入星球后，即可获取基于Jupyter Notebook的研究环境，直接运行代码。

在该环境中，除本文代码外，之前付费文章的代码也都在。并且，今后的文章只要声明附有代码和数据，可复现的，都能在此环境中找到。

  • 需要 2 分钟阅读时间

10 月 24 日，庆祝码农节！Python 刚刚发布了 3.13 版本

今天（10 月 24 日）是码农节。这一天也是裘伯君、Chris Lattner, Robert Khan 等人的生日。Lattner 是 LLVM 开源编译器的创始人、Swift 和 Mojo 语言的主要设计者。Khan 是互联网奠基人之一，他与温顿。瑟夫共同发明了 TCP/IP 协议。

不过，最令程序员兴奋的是，Python 3.13 正式版本发布了！

这个版本的重点是，引入了一个新的交互式解释器，并且对自由线程模型（PEP 703）和即时编译器（PEP 744）提供了实验性支持。这是 Python 程序员多少年以来，翘首以盼的性能改进！

REPL

新的交互式解释器这一功能可能会引起误解。它实际上指的是一个新的交互式 shell，而不是语言解释器本身。这个新的 shell 来自于 PyPy 项目。这个解释器支持彩色输出、多行编辑、历史回顾和多行粘贴模式。

Lattner 和 Mojo 语言。Mojo 号称比 Python 快 6.8 万倍

Python 的交互式 shell 一直是它的特色和优势，想了解一个函数的功能和用法，直接在终端中输入 ipython 之后，就可以立即尝试这个函数。我是常常拿 ipython 当计算器使用，特别方便。

JIT

从 3.11 起，Python 开始引进 JIT 的一些特性。在 Python 3.11 版本中，当解释器检测到某些操作涉及的类型总是相同的时候，这些操作就会被“专门化”，替换成特别的字节码，这使得代码中这部分区域的运行速度提升 10%到 25%。到了 3.13 版本，它已经能在运行时生成实际的机器代码，而不仅仅是专门的字节码。现在，提速还不是很明显，但为未来的优化铺平了道路。

不过，目前 JIT 还被认为是实验性的，默认情况下未启用。CPython 团队还在观察它对整个社区的影响，一旦成熟，就会成为默认选项。

Free Threaded CPython

Robert Kahn，互联网之父

之前大家讨论很久的无 GIL 版本，现在官方名称确定为 Free Threaded CPython。在这个版本下，CPython 允许线程完全并行运行。这将立刻数倍提升 Python 的性能。不过，目前该功能也是实验性的。

要启用这两个实验性的功能，你需要自己从源代码编译 CPython。同样地，这已经让人看到了曙光。而且，这个等待时间并不会太长，这些功能已经在 Meta 内部广泛使用了。

其它性能优化

这一版在 Windows 上，将提供精度为 1 微秒的计时器，而不再是过去精度只有 15.6 毫秒的时钟。这一变化将使得 Python 在 Windows 上将能执行一些实时任务。

之前 typing 库的部分模块会导致导入时间过长，现在，这个时间已减少了大约 1/3。当然，我们平常可能感受不出来，但如果你的程序会启动子进程来执行一些简短的计算密集型任务的话，这个区别就比较大了。

说到子进程，subprocess 现在会更多地使用 posix_spawn 函数创建子进程，这将带来一些性能上的提升。

弃用版本管理

在 Python 中，弃用版本管理一直是通过第三方库来实现的。现在，这一特性终于被内置了：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
from warnings import deprecated
from typing import overload

@deprecated("Use B instead")
class A:
    pass

@deprecated("Use g instead")
def f():
    pass

@overload
@deprecated("int support is deprecated")
def g(x: int) -> int: ...
@overload
def g(x: str) -> int: ...

不过，第三方库 deprecation 似乎仍然在功能上更胜一筹。这是 deprecation 的用法：

1
2
3
4
5
from deprecation import deprecated

@deprecated("2.0.0", details="use function `bar` instead")
def foo(*args):
    pass

你就是列文。虎克！

这是网上的一个梗，说的是有些人看图特别仔细，拿着显微镜找 bug。列文。虎克就是发明显微镜的人。10月24日也是他的生日。

列文。虎克裁缝学徒出身，没受过正规教育。后来成为一名布匹商，为了检验布匹的质量，他购买了放大镜来观察布匹的纤维，也由此开启了他的大国工匠之路（17 世纪的荷兰的确是大国。世界上的第一个证券交易所 -- 资本主义的标志，就诞生在 17 世纪的荷兰）。

列文。虎克没有受过正规训练，凭着兴趣和热爱，发明了显微镜，为人类打开了从未见过的世界。他的成就最终被英国皇家学会接受，在 1680 年当选为皇家学会成员。终其一生，他为这个世界留下的，除了他自己的名字，还有 cell 这个词。

“我总是尽力做到最好，即使是最小的事物也值得认真对待”。正是凭着这种信仰，他才得以见微知著，于一粒沙中发现宇宙。